Embora os métodos da seção anterior sejam úteis para descrever e exibir dados de amostra, o verdadeiro poder da estatística é revelado quando usamos amostras para nos dar informações sobre populações. Neste contexto, uma população é toda a colecção de objectos de interesse, por exemplo, os preços de venda de todas as casas unifamiliares no mercado habitacional representado pelo nosso conjunto de dados. Gostaríamos de saber mais sobre esta população para nos ajudar a tomar uma decisão sobre qual casa comprar, mas o único dado que temos é uma amostra aleatória de 30 preços de venda.
Antes disso, podemos empregar o “pensamento estatístico” para extrair inferências sobre a população de interesse, analisando os dados da amostra. Em particular, usamos a noção de um modelo – uma abstração matemática do mundo real – que se encaixa nos dados da amostra. Se este modelo fornece um ajuste razoável aos dados, ou seja, se ele pode aproximar a maneira como os dados variam, então assumimos que ele também pode aproximar o comportamento da população. O modelo então fornece a base para tomar decisões sobre a população, por exemplo, identificando padrões, explicando a variação e prevendo valores futuros. É claro que este processo só pode funcionar se os dados da amostra puderem ser considerados representativos da população.
Por vezes, mesmo quando sabemos que uma amostra não foi selecionada aleatoriamente, ainda podemos modelá-la. Então, podemos não ser capazes de inferir formalmente sobre uma população a partir da amostra, mas ainda podemos modelar a estrutura subjacente da amostra. Um exemplo seria uma amostra de conveniência – uma amostra selecionada mais por razões de conveniência do que por suas propriedades estatísticas. Ao modelar tais amostras, quaisquer resultados devem ser relatados com cuidado para restringir quaisquer conclusões a objetos similares aos da amostra. Outro tipo de exemplo é quando a amostra abrange toda a população. Por exemplo, poderíamos modelar dados para todos os 50 estados dos Estados Unidos da América para entender melhor quaisquer padrões ou associações sistemáticas entre os estados.
Desde que o mundo real pode ser extremamente complicado (na forma como os valores dos dados variam ou interagem juntos), os modelos são úteis porque simplificam os problemas para que possamos compreendê-los melhor (e depois tomar decisões mais eficazes). Por um lado, precisamos de modelos que sejam suficientemente simples para que possamos usá-los facilmente para tomar decisões, mas, por outro lado, precisamos de modelos que sejam flexíveis o suficiente para fornecer boas aproximações a situações complexas. Felizmente, muitos modelos estatísticos têm sido desenvolvidos ao longo dos anos que proporcionam um equilíbrio eficaz entre estes dois critérios. Um desses modelos, que fornece um bom ponto de partida para os modelos mais complicados que consideramos mais tarde, é a distribuição normal.
De uma perspectiva estatística, uma distribuição de probabilidade é um modelo teórico que descreve como uma variável aleatória varia. Para nossos propósitos, uma variável aleatória representa os valores dos dados de interesse da população, por exemplo, os preços de venda de todas as casas unifamiliares no nosso mercado habitacional. Uma forma de representar a distribuição da população de valores de dados está em um histograma, como descrito na Seção 1.1. A diferença agora é que o histograma exibe toda a população e não apenas a amostra. Como a população é muito maior que a amostra, as caixas do histograma (as faixas consecutivas dos dados que compõem os intervalos horizontais para as barras) podem ser muito menores, por exemplo, o seguinte mostra um histograma para uma população simulada de 1.000 preços de venda.
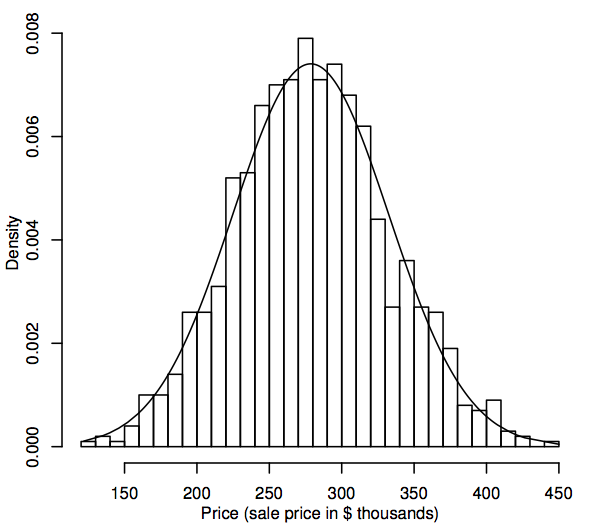
À medida que o tamanho da população fica maior, podemos imaginar as barras do histograma ficando mais finas e mais numerosas, até que o histograma se assemelha a uma curva suave ao invés de uma série de passos. Esta curva suave é chamada de curva de densidade e pode ser pensada como a versão teórica do histograma da população. As curvas de densidade também fornecem uma forma de visualizar as distribuições de probabilidade, como a distribuição normal. Uma curva de densidade normal é sobreposta ao histograma acima. O histograma simulado da população segue a curva bastante de perto, o que sugere que esta distribuição populacional simulada é bastante próxima da normal.
Para ver como uma distribuição teórica pode ser útil para fazer inferências estatísticas sobre populações como aquela em nosso exemplo de preços domésticos, precisamos olhar mais de perto para a distribuição normal. Para começar, consideramos uma versão particular da distribuição normal, a normal padrão, como representada pela seguinte curva de densidade.
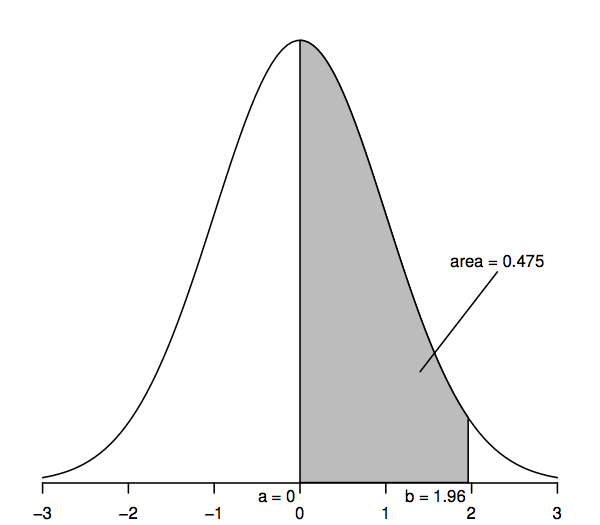
As variáveis aleatórias que seguem uma distribuição normal padrão têm uma média de 0 (assim a curva é simétrica em torno de 0, que está sob o ponto mais alto da curva) e um desvio padrão de 1 (assim a curva tem um ponto de inflexão – onde a curva se dobra primeiro de uma maneira e depois da outra – em +1 e -1). A curva de densidade normal é às vezes chamada de “curva do sino”, pois sua forma se assemelha à de um sino.
A característica chave da curva de densidade normal que nos permite fazer inferências estatísticas é que as áreas sob a curva representam probabilidades. A área inteira sob a curva é uma, enquanto a área sob a curva entre um ponto no eixo horizontal (a, digamos) e outro ponto (b, digamos) representa a probabilidade de que uma variável aleatória que segue uma distribuição normal padrão esteja entre a e b. Assim, por exemplo, a figura acima mostra que a probabilidade é 0.475 que uma variável aleatória normal padrão está entre a=0 e b=1,96, já que a área abaixo da curva entre a=0 e b=1,96 é 0,475,
Podemos obter valores para essas áreas ou probabilidades a partir de uma variedade de fontes: tabelas de números, calculadoras, planilhas eletrônicas ou software estatístico, websites, e assim por diante. Abaixo imprimimos apenas alguns valores selecionados já que a maioria dos cálculos posteriores utiliza uma generalização da distribuição normal chamada “t-distribuição”. Além disso, em vez de áreas como aquela sombreada na figura acima, será mais útil considerar “áreas de cauda” (por exemplo, à direita do ponto b), e assim para consistência com tabelas posteriores de números, a tabela seguinte permite calcular essas áreas de cauda:
Em particular, a área superior à direita de 1,96 é 0,025; isto equivale a dizer que a área entre 0 e 1,96 é 0,475 (uma vez que toda a área sob a curva é 1 e a área à direita de 0 é 0,5). Da mesma forma, a área de duas caudas, que é a soma das áreas à direita de 1,96 e à esquerda de -1,96, é duas vezes 0,025, ou 0,05,
Como tudo isso nos ajuda a fazer inferências estatísticas sobre as populações, como a do nosso exemplo de preços domésticos? A ideia essencial é que encaixamos um modelo de distribuição normal nos dados da nossa amostra e depois usamos este modelo para fazer inferências sobre a população correspondente. Por exemplo, podemos usar cálculos de probabilidade para uma distribuição normal (como mostrado na figura acima) para fazer declarações de probabilidade sobre uma população modelada usando essa distribuição normal – mostraremos exatamente como fazer isso na Seção 1.3. Antes de fazermos isso, porém, paramos para considerar um aspecto dessa seqüência inferencial que pode fazer ou quebrar o processo. O modelo fornece uma aproximação suficiente ao padrão de valores da amostra que podemos estar confiantes de que o modelo representa adequadamente os valores da população? Quanto melhor a aproximação, mais confiáveis serão as nossas afirmações inferenciais.
Vimos anteriormente como uma curva de densidade pode ser pensada como um histograma com um tamanho de amostra muito grande. Assim, uma maneira de avaliar se nossa população segue um modelo de distribuição normal é construir um histograma a partir dos dados de nossa amostra e determinar visualmente se ele “parece normal”, ou seja, aproximadamente simétrico e em forma de sino. Esta é uma decisão um pouco subjetiva, mas com a experiência você deve descobrir que se torna mais fácil discernir histogramas claramente não-normais daqueles que são razoavelmente normais. Por exemplo, enquanto o histograma acima parece claramente uma curva de densidade normal, a normalidade do histograma de 30 amostras de preços de venda na Secção 1.1 é menos certa. Uma conclusão razoável neste caso seria que embora este histograma da amostra não seja perfeitamente simétrico e em forma de sino, é suficientemente próximo de que o histograma da população correspondente (hipotético) poderia muito bem ser normal.
Uma forma alternativa de avaliar a normalidade é construir um gráfico QQ (quantil-quantil), também conhecido como gráfico de probabilidade normal, como mostrado aqui para os dados de preços domésticos:
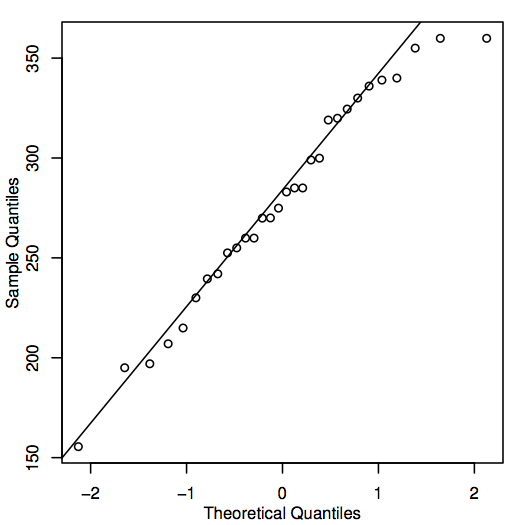
Se os pontos do gráfico QQ estiverem próximos da linha diagonal, então os valores populacionais correspondentes poderiam muito bem ser normais. Se os pontos geralmente se encontram longe da linha, então a normalidade está em questão. Mais uma vez, esta é uma decisão um pouco subjetiva que se torna mais fácil de fazer com a experiência. Neste caso, dado o tamanho relativamente pequeno da amostra, os pontos provavelmente estão suficientemente próximos da linha que é razoável concluir que os valores populacionais poderiam ser normais.
Há também uma variedade de métodos quantitativos para avaliar a normalidade – ver Secção 6.3.