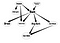
Bayesian Belief Network ou Bayesian Network ou Belief Network é um Modelo Gráfico Probabilístico (PGM) que representa dependências condicionais entre variáveis aleatórias através de um Gráfico Acíclico Direcionado (DAG).
>
Hoje vou tentar explicar os principais aspectos das Redes de Crenças, especialmente para aplicações que possam estar relacionadas com a Análise de Redes Sociais (SNA). Além disso, vou mostrar um exemplo de implementação deste tipo de rede.
Para que usamos as Redes Bayesianas?
As Redes Bayesianas são aplicadas em muitos campos. Por exemplo, diagnóstico de doenças, busca otimizada na web, filtragem de spam, redes reguladoras de genes, etc. E esta lista pode ser estendida. O principal objetivo destas redes é tentar entender a estrutura das relações de causalidade. Para esclarecer isto, vamos considerar um problema de diagnóstico de doenças. Com determinados sintomas e sua doença resultante, construímos nossa Rede de Crenças e quando um novo paciente chega, podemos inferir qual doença ou doenças podem ter o novo paciente, fornecendo probabilidades para cada doença. Da mesma forma, essas relações de causalidade podem ser construídas para outros problemas e técnicas de inferência podem ser aplicadas a resultados interessantes.
Revisão Rápida da Probabilidade
Antes de continuar, para refrescar nossas memórias, deixe-me dar-lhe a definição de propriedade condicional. Probabilidade condicional é a probabilidade de uma variável aleatória quando alguma outra variável aleatória é dada. É mostrado por
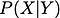
>
Se estas duas variáveis aleatórias são dependentes,
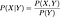 >
>
>
>
Se elas são independentes, então
>
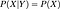
>>
Definição Matemática de Redes de Crenças
>
As probabilidades são calculadas nas redes de crenças pela seguinte fórmula
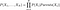
Como você entenderia pela fórmula, para podermos calcular a distribuição conjunta, precisamos de ter probabilidades condicionais indicadas pela rede. Mas além disso, se tivermos a distribuição conjunta, então podemos começar a fazer perguntas interessantes. Por exemplo, no primeiro exemplo, pedimos a probabilidade de “RAIN” se “SEASON” for “WINTER” e “DOG BARK” for “TRUE”.
Python Example of Belief Network
Então, acho isto suficiente para a teoria e vamos ver um exemplo real com a minha actual linguagem de programação favorita Python ❤️ Antes de continuar, pode encontrar o Jupyter Notebook que escrevi aqui.
# create the nodes
season = BbnNode(Variable(0, 'season', ), )
atmos_pres = BbnNode(Variable(1, 'atmos_press', ), )
allergies = BbnNode(Variable(2, 'allergies', ), )
rain = BbnNode(Variable(3, 'rain', ), )
grass = BbnNode(Variable(4, 'grass', ), )
umbrellas = BbnNode(Variable(5, 'umbrellas', ), )
dog_bark = BbnNode(Variable(6, 'dog_bark', ), )
cat_mood = BbnNode(Variable(7, 'cat_mood', ), )
cat_hide = BbnNode(Variable(8, 'cat_hide', ), )bbn = Bbn() \
.add_node(season) \
.add_node(atmos_pres) \
.add_node(allergies) \
.add_node(rain) \
.add_node(grass) \
.add_node(umbrellas) \
.add_node(dog_bark) \
.add_node(cat_mood) \
.add_node(cat_hide) \
.add_edge(Edge(season, allergies, EdgeType.DIRECTED)) \
.add_edge(Edge(season, umbrellas, EdgeType.DIRECTED)) \
.add_edge(Edge(season, rain, EdgeType.DIRECTED)) \
.add_edge(Edge(atmos_pres, rain, EdgeType.DIRECTED)) \
.add_edge(Edge(rain, grass, EdgeType.DIRECTED)) \
.add_edge(Edge(rain, umbrellas, EdgeType.DIRECTED)) \
.add_edge(Edge(rain, dog_bark, EdgeType.DIRECTED)) \
.add_edge(Edge(rain, cat_mood, EdgeType.DIRECTED)) \
.add_edge(Edge(dog_bark, cat_hide, EdgeType.DIRECTED)) \
.add_edge(Edge(cat_mood, cat_hide, EdgeType.DIRECTED))
Descrevemos primeiro os nossos nós com probabilidades condicionais. Você deve notar que eu pulei alguns valores de estado possíveis por simplicidade. Por exemplo, a variável de estação toma outros valores “primavera” e “outono”. Então, a idéia é a mesma.
Não, vamos verificar se nossa rede está construída corretamente ou não.
with warnings.catch_warnings():
warnings.simplefilter('ignore')
graph = convert_for_drawing(bbn)
pos = nx.nx_agraph.graphviz_layout(graph, prog='neato')plt.figure(figsize=(20, 10))
plt.subplot(121)
labels = dict()
nx.draw(graph, pos=pos, with_labels=True, labels=labels)
plt.title('BBN DAG')
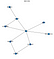
Este trecho de código resultaria no seguinte gráfico
>
>
>
Então, você vê que esta rede se encaixa no meu desenho extravagante no início. Agora, vamos fazer algumas inferências sobre esta Belief Network.
# convert the BBN to a join tree
join_tree = InferenceController.apply(bbn)# insert an observation evidence
ev = EvidenceBuilder() \
.with_node(join_tree.get_bbn_node_by_name('season')) \
.with_evidence('winter', 1.0) \
.build()join_tree.set_observation(ev)# print the marginal probabilities
for node in join_tree.get_bbn_nodes():
potential = join_tree.get_bbn_potential(node)
print(node)
print(potential)
print('--------------------->')
Este trecho de código basicamente dá evidências para a rede que é a estação do inverno com 1.0 de probabilidade. De acordo com esta evidência, quando fazemos a inferência, obtemos os seguintes resultados.
0|season|winter,summer
0=winter|1.00000
0=summer|0.00000
--------------------->
2|allergies|allergic,non_alergic
2=allergic|0.70000
2=non_alergic|0.30000
--------------------->
3|rain|rainy,sunny
3=rainy|0.80000
3=sunny|0.20000
--------------------->
4|grass|grass,no_grass
4=grass|0.70000
4=no_grass|0.30000
--------------------->
1|atmos_press|high,low
1=high|0.50000
1=low|0.50000
--------------------->
5|umbrellas|on,off
5=on|0.95200
5=off|0.04800
--------------------->
6|dog_bark|bark,not_bark
6=bark|0.66000
6=not_bark|0.34000
--------------------->
7|cat_mood|good,bad
7=good|0.23000
7=bad|0.77000
--------------------->
8|cat_hide|hide,show
8=hide|0.87150
8=show|0.12850
--------------------->
Quando adicionamos mais evidências, como se o cão não estivesse ladrando
# convert the BBN to a join tree
join_tree = InferenceController.apply(bbn)# insert an observation evidence
ev = EvidenceBuilder() \
.with_node(join_tree.get_bbn_node_by_name('season')) \
.with_evidence('winter', 1.0) \
.build()ev2 = EvidenceBuilder() \
.with_node(join_tree.get_bbn_node_by_name('dog_bark')) \
.with_evidence('not_bark', 1.0) \
.build()join_tree.set_observation(ev)
join_tree.set_observation(ev2)# print the marginal probabilities
for node in join_tree.get_bbn_nodes():
potential = join_tree.get_bbn_potential(node)
print(node)
print(potential)
print('--------------------->')
Obtemos os seguintes resultados de inferência
0|season|winter,summer
0=winter|1.00000
0=summer|0.00000
--------------------->
2|allergies|allergic,non_alergic
2=allergic|0.70000
2=non_alergic|0.30000
--------------------->
3|rain|rainy,sunny
3=rainy|0.47059
3=sunny|0.52941
--------------------->
4|grass|grass,no_grass
4=grass|0.53529
4=no_grass|0.46471
--------------------->
1|atmos_press|high,low
1=high|0.39706
1=low|0.60294
--------------------->
5|umbrellas|on,off
5=on|0.88941
5=off|0.11059
--------------------->
6|dog_bark|bark,not_bark
6=bark|0.00000
6=not_bark|1.00000
--------------------->
7|cat_mood|good,bad
7=good|0.52647
7=bad|0.47353
--------------------->
8|cat_hide|hide,show
8=hide|0.83162
8=show|0.16838
--------------------->
Você vê a diferença? 😆 Muitos valores de probabilidade mudaram quando adicionamos a evidência relacionada com o latido. É definitivamente um exemplo bobo, mas bom para obter intuição.
Como usar as Redes Bayesianas no SNA ?
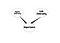
As Redes Bayesianas são ferramentas muito poderosas para entender a estrutura das relações de causalidade entre as variáveis. Uma vez projetado o seu modelo, mesmo com um pequeno conjunto de dados, ele pode lhe dizer várias coisas. A questão nesta parte é como obter o benefício das Redes Bayesianas em SNA. A resposta não é única, mas vamos começar com uma idéia profunda. No SNA, nós tentamos entender a estrutura de uma rede social. Além disso, tentamos entender a importância dos nós. Mas não sabemos quais são os resultados da nossa métrica de importância. Este é o ponto onde as Redes Bayesianas acontecem. Por exemplo, se você acha que a importância de um nó é causada pela Centralidade de Graus e Centralidade de Links, você pode ter a seguinte rede.
>
>
Esta é uma Rede Bayesiana muito ingênua. Além de determinar a importância dos nós, outras aplicações podem estar procurando por algum tipo específico de nós. Vamos considerar uma Rede Social na qual existem algumas pessoas que são líderes potenciais e eu quero procurá-los. Considere o seguinte gráfico
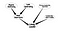
>
>
Esta rede um pouco mais complicada nos ajudará a determinar a incerteza dos nós relacionados a ser uma liderança.
Outra aplicação seria inferir os links. Os novos links podem ser inferidos a partir de links já existentes. Por exemplo, a partir da adesão do grupo a uma Rede Social, é possível inferir um provável link de adesão. O que eu quis dizer é que podemos modelar um novo link entre usuários e grupos, considerando os links existentes. Veja o seguinte diagrama modelo
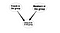
>
>
Então, estes são alguns exemplos básicos de como as Redes Bayesianas podem ser aplicadas no SNA. Este tópico não é estudado muito bem, mas acho que pode ser muito útil estudar mais a fundo.
Conclusão
O difícil sobre Bayesian Networks é projetar. Especialmente, quando você faz o SNA, construir mapeamento de Redes Sociais com uma Rede Bayesian é arte do que ciência 😃 Mas uma vez que você fez o trabalho de arte e projetou seu modelo muito bem, estas ferramentas úteis podem lhe dizer muitas coisas. Como sabemos que as Redes Bayesianas são aplicadas em vastos tipos de ares. Funcionou muito bem na maioria dos casos. Portanto, acredito firmemente que podemos fazer inferências muito profundas sobre Redes Sociais, também.
Para mais investigações com o SNA e Bayesian Networks, por favor fique atento 🚀