Classificação é uma abordagem supervisionada de aprendizagem de máquinas, na qual o algoritmo aprende com os dados que lhe são fornecidos – e depois usa esta aprendizagem para classificar novas observações.
Em outras palavras, o conjunto de dados de treino é usado para obter melhores condições de limite que podem ser usadas para determinar cada classe alvo; uma vez que tais condições de limite são determinadas, a próxima tarefa é prever a classe alvo.
Os classificadores binários trabalham com apenas duas classes ou resultados possíveis (exemplo: sentimento positivo ou negativo; se o emprestador pagará empréstimo ou não; etc.), e os classificadores Multiclasse trabalham com múltiplas classes (ex: a que país uma bandeira pertence, se uma imagem é uma maçã ou uma banana ou laranja; etc.). Multiclasse assume que cada amostra é atribuída a uma e apenas uma etiqueta.

Um dos primeiros algoritmos populares de classificação na aprendizagem de máquinas foi Naive Bayes, um classificador probabilístico inspirado no teorema de Bayes (que nos permite fazer uma dedução fundamentada dos eventos que acontecem no mundo real com base no conhecimento prévio de observações que possam implicá-lo). O nome (“Naive”) deriva do fato de que o algoritmo assume que os atributos são condicionalmente independentes.
O algoritmo é um algoritmo simples de implementar e geralmente representa um método razoável para dar início aos esforços de classificação. Ele pode facilmente escalar para conjuntos de dados maiores (leva tempo linear versus aproximação iterativa, como usado para muitos outros tipos de classificadores, que é mais caro em termos de recursos de computação) e requer pequena quantidade de dados de treinamento.
No entanto, Naive Bayes pode sofrer de um problema conhecido como ‘ problema de probabilidade zero ‘, quando a probabilidade condicional é zero para um determinado atributo, falhando em fornecer uma previsão válida. Uma solução é utilizar um procedimento de suavização (ex: método Laplace).

P(c|x) é a probabilidade posterior de classe (c, alvo) dado preditor (x, atributos). P(c) é a probabilidade anterior de classe. P(x|c) é a probabilidade que é a probabilidade do preditor dada classe, e P(x) é a probabilidade anterior do preditor.
O primeiro passo do algoritmo é calcular a probabilidade anterior para rótulos de classe dada. Em seguida, encontrar a probabilidade de probabilidade com cada atributo, para cada classe. Em seguida, colocar esses valores na fórmula de Bayes & calculando a probabilidade posterior, e então ver qual classe tem uma probabilidade maior, dado que o input pertence à classe de probabilidade maior.
É bastante simples implementar Naive Bayes em Python alavancando a biblioteca scikit-learn. Na verdade existem três tipos de modelo Naive Bayes sob a biblioteca scikit-learn: (a) Tipo gaussiano (assume que as características seguem uma distribuição normal, como um sino), (b) Multinomial (usado para contagens discretas, em termos de quantidade de vezes que um resultado é observado em x ensaios), e (c] Bernoulli (útil para vetores de características binárias; caso de uso popular é a classificação de texto).
Outro mecanismo popular é a árvore de decisão. Dado um dado de atributos juntamente com suas classes, a árvore produz uma seqüência de regras que podem ser usadas para classificar os dados. O algoritmo divide a amostra em dois ou mais conjuntos homogêneos (folhas) com base nos diferenciadores mais significativos nas variáveis de entrada. Para escolher um diferenciador (preditor), o algoritmo considera todas as características e faz uma divisão binária sobre elas (para dados categóricos, divididos por gato; para contínuo, escolha um limite de corte). Ele então escolherá aquele com menor custo (ou seja, maior precisão), repetindo recursivamente, até dividir com sucesso os dados em todas as folhas (ou atingir a profundidade máxima).
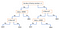
Árvores de decisão são em geral simples de entender e visualizar, requerendo pouca preparação de dados. Este método também pode lidar com dados numéricos e categóricos. Por outro lado, árvores complexas não generalizam bem (“overfitting”), e árvores de decisão podem ser um pouco instáveis porque pequenas variações nos dados podem resultar na geração de uma árvore completamente diferente.
Um método de classificação derivado de árvores de decisão é o Random Forest, essencialmente um “meta-estimador” que se encaixa em várias subamostras de conjuntos de dados e usa a média para melhorar a precisão preditiva do modelo e controla o excesso de ajuste. O tamanho da subamostra é o mesmo que o tamanho da amostra de entrada original – mas as amostras são desenhadas com substituição.
As Florestas Aleatórias tendem a exibir maior grau de robustez ao sobreajuste (>robustez ao ruído nos dados), com tempo de execução eficiente mesmo em conjuntos de dados maiores. No entanto, são mais sensíveis a conjuntos de dados desequilibrados, sendo também um pouco mais complexos de interpretar e exigindo mais recursos computacionais.
Outro classificador popular no ML é o Logistic Regression – onde probabilidades descrevendo os possíveis resultados de um único estudo são modeladas usando uma função logística (método de classificação apesar do nome):

Aqui está como é a equação logística:
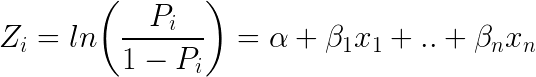
>
E (expoente) em ambos os lados da equação resulta:
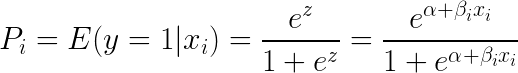
Regressão Lógica é mais útil para compreender a influência de várias variáveis independentes em uma única variável de resultado. Ela é focada na classificação binária (para problemas com múltiplas classes, usamos extensões de regressão logística como a regressão logística multinomial e ordinal). Regressão logística é popular entre casos de uso – como análise de crédito e propensão a responder/comprar.
Last mas não menos importante, kNN (para “k Vizinhos mais próximos”) também é freqüentemente usado para problemas de classificação. kNN é um algoritmo simples que armazena todos os casos disponíveis e classifica novos casos com base em uma medida de similaridade (por exemplo, funções de distância). Tem sido usado na estimativa estatística e reconhecimento de padrões já no início dos anos 70 como uma técnica não paramétrica:

