Introdução

Imprensa isto – Você foi encarregado de prever o preço do próximo iPhone e foram-lhe fornecidos dados históricos. Isto inclui características como vendas trimestrais, gastos mês a mês e uma série de coisas que vêm com o balanço da Apple. Como cientista de dados, que tipo de problema você classificaria isso como? Modelagem de séries cronológicas, claro.

Da previsão das vendas de um produto à estimativa do consumo de eletricidade das residências, a previsão de séries cronológicas é uma das principais habilidades que qualquer cientista de dados deve conhecer, se não dominar. Há uma infinidade de técnicas diferentes por aí que você pode usar, e nós estaremos cobrindo uma das mais eficazes, chamada Auto ARIMA, neste artigo.

Primeiro vamos entender o conceito de ARIMA que nos levará ao nosso tópico principal – Auto ARIMA. Para solidificar os nossos conceitos, vamos pegar num conjunto de dados e implementá-lo tanto em Python como em R.

Tabela de conteúdo

1. O que é uma série temporal?
2. Métodos de previsão de séries temporais
3. Introdução ao ARIMA
4. Passos para implementação do ARIMA
5. Porquê precisamos do Auto ARIMA?
6. Auto implementação ARIMA (no conjunto de dados de passageiros aéreos)
7. Como é que o Auto ARIMA selecciona parâmetros?

Se está familiarizado com as séries temporais e as suas técnicas (como média móvel, suavização exponencial e ARIMA), pode saltar directamente para a secção 4. Para iniciantes, comece pela seção abaixo que é uma breve introdução a séries cronológicas e várias técnicas de previsão.

O que é uma série cronológica ?

Antes de aprendermos sobre as técnicas para trabalhar com dados de séries cronológicas, devemos primeiro entender o que é realmente uma série cronológica e como ela é diferente de qualquer outro tipo de dado. Aqui está a definição formal de séries cronológicas – É uma série de pontos de dados medidos em intervalos de tempo consistentes. Isto significa simplesmente que determinados valores são registrados em um intervalo constante que pode ser horário, diário, semanal, a cada 10 dias, e assim por diante. O que torna as séries cronológicas diferentes é que cada ponto de dados na série depende dos pontos de dados anteriores. Vamos entender a diferença mais claramente tomando alguns exemplos.

Exemplo 1:

Suponha que você tenha um conjunto de dados de pessoas que tenham contraído um empréstimo de uma determinada empresa (como mostrado na tabela abaixo). Você acha que cada linha estará relacionada com as linhas anteriores? Certamente que não! O empréstimo feito por uma pessoa será baseado em suas condições financeiras e necessidades (pode haver outros fatores como o tamanho da família, etc., mas por simplicidade estamos considerando apenas renda e tipo de empréstimo) . Além disso, os dados não foram coletados em nenhum intervalo de tempo específico. Depende de quando a empresa recebeu um pedido de empréstimo.

Exemplo 2:

Vamos dar outro exemplo. Suponha que você tenha um conjunto de dados que contenha o nível de CO2 no ar por dia (captura de tela abaixo). Você será capaz de prever a quantidade aproximada de CO2 para o dia seguinte, olhando para os valores dos últimos dias? Bem, é claro. Se você observar, os dados foram registrados diariamente, ou seja, o intervalo de tempo é constante (24 horas).

Você já deve ter tido uma intuição sobre isso – o primeiro caso é um simples problema de regressão e o segundo é um problema de série temporal. Embora o quebra-cabeça das séries cronológicas aqui também possa ser resolvido usando a regressão linear, mas essa não é realmente a melhor abordagem, pois negligencia a relação dos valores com todos os valores relativos do passado. Vamos agora olhar para algumas das técnicas comuns usadas para resolver problemas de séries cronológicas.

Métodos para previsão de séries cronológicas

Existem vários métodos para previsão de séries cronológicas e iremos cobri-los brevemente nesta seção. A explicação detalhada e os códigos python para todas as técnicas mencionadas abaixo podem ser encontrados neste artigo: 7 técnicas para previsão de séries cronológicas (com códigos python).

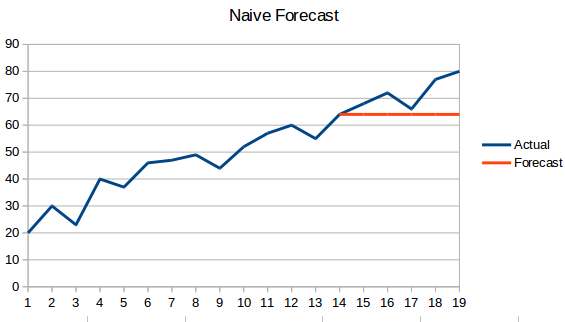
1. Abordagem ingênua: Nesta técnica de previsão, o valor do novo ponto de dados é previsto para ser igual ao ponto de dados anterior. O resultado seria uma linha plana, já que todos os novos valores tomam os valores anteriores.
2. Média Simples: O próximo valor é tomado como a média de todos os valores anteriores. As previsões aqui são melhores que a ‘Abordagem Naïf’, pois não resulta em uma linha plana, mas aqui, todos os valores passados são levados em consideração, o que pode nem sempre ser útil. Por exemplo, quando se pede para prever a temperatura de hoje, você consideraria a temperatura dos últimos 7 dias em vez da temperatura de um mês atrás.
3. Moving Average : Esta é uma melhoria em relação à técnica anterior. Ao invés de tomar a média de todos os pontos anteriores, a média de ‘n’ pontos anteriores é tomada como o valor previsto.
4. Média móvel ponderada : Uma média móvel ponderada é uma média móvel onde os valores ‘n’ anteriores recebem pesos diferentes.
5. Alisamento Exponencial Simples: Nesta técnica, pesos maiores são atribuídos a observações mais recentes do que a observações do passado distante.
6. Modelo de Tendência Linear de Holt: Este método leva em conta a tendência do conjunto de dados. Por tendência, entendemos a natureza crescente ou decrescente da série. Suponha que o número de reservas em um hotel aumenta a cada ano, então podemos dizer que o número de reservas mostra uma tendência crescente. A função de previsão neste método é uma função de nível e tendência.
7. Método Holt Winters: Este algoritmo leva em conta tanto a tendência como a sazonalidade da série. Por exemplo – o número de reservas num hotel é alto nos fins de semana & baixo nos dias de semana, e aumenta a cada ano; existe uma sazonalidade semanal e uma tendência crescente.
8. ARIMA: ARIMA é uma técnica muito popular para a modelagem de séries temporais. Ela descreve a correlação entre os pontos de dados e leva em conta a diferença dos valores. Uma melhoria em relação a ARIMA é a SARIMA (ou ARIMA sazonal). Vamos ver ARIMA com um pouco mais de detalhe na secção seguinte.

Introdução a ARIMA

Nesta secção vamos fazer uma introdução rápida a ARIMA que será útil na compreensão do Auto Arima. Uma explicação detalhada do Arima, parâmetros (p,q,d), parcelas (ACF PACF) e implementação está incluída neste artigo : Tutorial completo para séries cronológicas.

ARIMA é um método estatístico muito popular para a previsão de séries cronológicas. ARIMA significa Auto-Regressive Integrated Moving Averages (Médias Móveis Integradas Auto-Regressivas). Os modelos ARIMA trabalham com as seguintes hipóteses –

• As séries de dados são estacionárias, o que significa que a média e a variância não devem variar com o tempo. Uma série pode ser estacionária usando transformação de log ou diferindo a série.
• Os dados fornecidos como entrada devem ser uma série univariada, já que a arima usa os valores passados para prever os valores futuros.

ARIMA tem três componentes – AR (termo autoregressivo), I (termo diferencial) e MA (termo médio móvel). Vamos entender cada um destes componentes –

• AR termo refere-se aos valores passados usados para prever o próximo valor. O termo AR é definido pelo parâmetro ‘p’ em arima. O valor de ‘p’ é determinado usando o gráfico PACF.
• termo AR é usado para definir o número de erros de previsão passados usados para prever os valores futuros. O parâmetro ‘q’ em arima representa o termo MA. O gráfico ACF é usado para identificar o valor ‘q’ correto.
• Ordem de diferenciação especifica o número de vezes que a operação de diferenciação é executada em série para torná-la estacionária. Teste como ADF e KPSS pode ser usado para determinar se a série é estacionária e ajuda na identificação do valor d.

Passos para implementação ARIMA

Os passos gerais para implementar um modelo ARIMA são –

1. Carregar os dados: O primeiro passo para a construção do modelo é, naturalmente, carregar o conjunto de dados
2. Pré-processamento: Dependendo do conjunto de dados, os passos do pré-processamento serão definidos. Isto incluirá a criação de carimbos temporais, a conversão do tipo de coluna data/hora, a univariação das séries, etc.
3. Tornar as séries estacionárias: A fim de satisfazer a suposição, é necessário tornar a série estacionária. Isto incluiria verificar a estacionaridade da série e realizar as transformações necessárias
4. Determinar o valor d: Para tornar a série estacionária, o número de vezes que a operação de diferença foi realizada será tomado como o valor d
5. Criar gráficos ACF e PACF: Este é o passo mais importante na implementação do ARIMA. Os gráficos ACF PACF são utilizados para determinar os parâmetros de entrada para nosso modelo ARIMA
6. Determinar os valores p e q: Ler os valores de p e q dos lotes no passo anterior
7. Ajustar o modelo ARIMA: Utilizando os dados processados e os valores dos parâmetros calculados a partir dos passos anteriores, ajustar o modelo ARIMA
8. Prever valores no conjunto de validação: Prever os valores futuros
9. Calcular RMSE: Para verificar o desempenho do modelo, verificar o valor RMSE utilizando as previsões e os valores reais no conjunto de validação

Por que precisamos do Auto ARIMA?

Embora o ARIMA seja um modelo muito poderoso para prever dados de séries temporais, os processos de preparação de dados e de ajuste de parâmetros acabam por ser realmente demorados. Antes de implementar o ARIMA, você precisa tornar as séries estacionárias, e determinar os valores de p e q usando os gráficos que discutimos acima. O Auto ARIMA torna esta tarefa realmente simples para nós, pois elimina os passos 3 a 6 que vimos na seção anterior. Abaixo estão os passos que você deve seguir para implementar o auto ARIMA:

1. Load os dados: Este passo será o mesmo. Carregue os dados em seu notebook
2. Pré-processar os dados: A entrada deve ser univariada, portanto solte as outras colunas
3. Fit Auto ARIMA: Ajuste o modelo na série univariada
4. Prever valores no conjunto de validação: Fazer previsões no conjunto de validação
5. Calcular RMSE: Verificar o desempenho do modelo usando os valores previstos em relação aos valores reais

Foramos completamente a seleção da característica p e q como você pode ver. Que alívio! Na próxima seção, vamos implementar o auto ARIMA usando um conjunto de dados do brinquedo.

Implementação em Python e R

Usaremos o conjunto de dados do International-Air-Passenger. Este conjunto de dados contém o total mensal do número de passageiros (em milhares). Ele tem duas colunas – mês e contagem de passageiros. Você pode baixar o conjunto de dados deste link.

#load the datadata = pd.read_csv('international-airline-passengers.csv')#divide into train and validation settrain = datavalid = data#preprocessing (since arima takes univariate series as input)train.drop('Month',axis=1,inplace=True)valid.drop('Month',axis=1,inplace=True)#plotting the datatrain.plot()valid.plot()

#building the modelfrom pyramid.arima import auto_arimamodel = auto_arima(train, trace=True, error_action='ignore', suppress_warnings=True)model.fit(train)forecast = model.predict(n_periods=len(valid))forecast = pd.DataFrame(forecast,index = valid.index,columns=)#plot the predictions for validation setplt.plot(train, label='Train')plt.plot(valid, label='Valid')plt.plot(forecast, label='Prediction')plt.show()

#calculate rmsefrom math import sqrtfrom sklearn.metrics import mean_squared_errorrms = sqrt(mean_squared_error(valid,forecast))print(rms)

output -76.51355764316357

Below é o código R para o mesmo problema:

# loading packageslibrary(forecast)library(Metrics)# reading datadata = read.csv("international-airline-passengers.csv")# splitting data into train and valid setstrain = datavalid = data# removing "Month" columntrain$Month = NULL# training modelmodel = auto.arima(train)# model summarysummary(model)# forecastingforecast = predict(model,44)# evaluationrmse(valid$International.airline.passengers, forecast$pred)

Como o Auto Arima seleciona os melhores parâmetros

No código acima, nós simplesmente usamos o código .fit() para caber no modelo sem ter que selecionar a combinação de p, q, d. Mas como o modelo descobriu a melhor combinação desses parâmetros? Auto ARIMA leva em conta os valores AIC e BIC gerados (como você pode ver no código) para determinar a melhor combinação de parâmetros. Os valores AIC (Akaike Information Criterion) e BIC (Bayesian Information Criterion) são estimadores para comparar os modelos. Quanto menores estes valores, melhor é o modelo.

Cheque estes links se você estiver interessado nas matemáticas por trás do AIC e BIC.

End Notes and Further Reads

Encontrou que o auto ARIMA é a técnica mais simples para a realização de previsões de séries temporais. Conhecer um atalho é bom, mas estar familiarizado com a matemática por trás dele também é importante. Neste artigo, eu folheei os detalhes de como funciona o ARIMA, mas certifique-se de que você passa pelos links fornecidos no artigo. Para sua fácil referência, aqui estão os links novamente:

• Um Guia Abrangente para iniciantes na Previsão de Séries Temporais em Python
• Tutorial Completo para Séries Temporais em R
• 7 técnicas para previsão de séries temporais (com códigos python)

Eu sugeriria praticar o que aprendemos aqui sobre este problema de prática: Problema de Prática de Séries Temporais. Você também pode fazer nosso curso de treinamento criado sobre o mesmo problema de prática, Previsão de séries cronológicas, para lhe dar um avanço.