(IUCr) Símbolos para elementos de simetria

Acta Cryst. (1992). A48, 727-732

Final report of the International Union of Crystallography Ad-Hoc Committee on the nomenclature of symmetry*

Por P. M. DE WOLFF (Presidente), Meermanstraat 126, 2614 AM Delft, The Netherlands,

Y. BILLIET, Ecole Nationale d’Ingénieurs, BPW 3038 Sfax, Tunesië,

J. D. H. DONNAY, Departamento de Ciências Geológicas, Universidade McGill, 3450 University Street, Montreal, Canadá H3A 2A7,

W. FISCHER, Institut für Mineralogie, Petrologie und Kristallographie der Phillips-Universität, Lahnberge, D-3550 Marburg (Lahn), Alemanha,

R. B. GALIULIN, Instituto de Cristalografia, Academia de Ciências da Rússia, Leninsky Prospekt 59, Moscou 117333, Rússia,

A. M. GLAZER, Laboratório Clarendon, Universidade de Oxford, Parks Road, Oxford OX1 3PU Inglaterra,

TH. HAHN, Institut für Kristallographie, RWTH, Templergraben 55, D-5100 Aachen, Alemanha,

MARJORIE SENECHAL, Departamento de Matemática, Smith College, Northampton, MA 01063, EUA,

D. P. SHOEMAKER, Departamento de Química, Oregon State University, OR 97331, EUA,

H. WONDRATSCHEK, Institut für Kristallographie, Universität Karlsruhe, Kaiserstrasse 12, D-7500 Karlsruhe 1, Alemanha,

A. J. C. WILSON (ex officio, IUCr Commission on International Tables), Crystallographic Data Centre, University Chemistry Laboratory, Lensfield Road, Cambridge CB2 1EW, Inglaterra

AND S. C. ABRAHAMS (ex officio, IUCr Commission on Crystallographic Nomenclature), Department of Physics, Southern Oregon State College, 1250 Siskiyou Boulevard, Ashland, OR 97520-5047, USA

(Recebido em 7 de novembro de 1991; aceito em 9 de março de 1992)

* Nomeado em 14 de novembro de 1984, modificado em 10 de agosto de 1987 sob as regras básicas delineadas na Acta Cryst. (1979), A35, 1072. Relatório Final aceito em 23 de dezembro de 1991 pela Comissão de Nomenclatura Cristalográfica do IUCr e 9 de março de 1992 pelo Comitê Executivo.

Abstract

Símbolos impressos novos ou redefinidos são propostos à luz da redefinição de elementos de simetria recentemente aceita. Em particular, a letra e cobre certos planos de planeio que até agora não tinham um símbolo único, como os chamados ‘a ou b’. O uso de e no símbolo Hermann-Mauguin de cinco grupos espaciais diferentes é recomendado. Para planos e projetados em uma direção paralela ao plano, é proposto um símbolo gráfico que elimina a ambigüidade de sua designação atual. A letra k é proposta para uma nova classe definida de planos de planeio que até agora estavam sem símbolo específico. Os símbolos para operações de simetria introduzidos nas descrições de grupos espaciais das Tabelas Internacionais de Cristalografia (1989), Vol. A (Dordrecht: Kluwer Academic Publishers) são recomendados para uso geral, com modificações apenas para operações de reflexão de planeio.

Introdução

O Comitê Ad-hoc nomeado em 1980 para considerar ‘problemas de nomenclatura relativos a operações de simetria e elementos de simetria em grupos espaciais’ emitiu dois Relatórios intitulados Nomenclatura para Famílias de Cristal, Tipos de Bravais-Latística e Classes Aritméticas (de Wolff et al., 1985) e Definição de Elementos de Simetria em Grupos Espaciais e Grupos de Pontos (de Wolff et al., 1989). Como observado no Relatório de 1989, o único problema pendente em relação às operações de simetria é o de escolher símbolos apropriados, uma vez que o conceito é claro. Uma notação provisória foi adotada nas Tabelas Internacionais de Cristalografia (1983, 1989), doravante referidas como ITA83.

Símbolos impressos para elementos de simetria

A definição de elementos de simetria como dada no Relatório de 1989 (de Wolff et al.) será utilizada ao longo do presente Relatório. Aqui repetimos a essência:

Para qualquer operação de simetria dada o seu elemento geométrico (plano, ponto e/ou linha) é definido. Um elemento de simetria é a combinação do elemento geométrico de uma das operações de simetria em um dado grupo espacial com o conjunto (chamado ‘conjunto de elementos’) de todas as operações de simetria nesse grupo espacial que compartilham esse elemento geométrico.

Definições explícitas dos elementos geométricos e descrições dos elementos de simetria resultantes, bem como seus símbolos, são dadas nas Tabelas 1 e 2. (Estas são idênticas às Tabelas 1 e 2 do Relatório de 1989, exceto para os planos de planeio, e são repetidas aqui para a completude, veja abaixo). Cada elemento de simetria é representado por um símbolo composto por dois caracteres. O primeiro caractere é um E maiúsculo para todos os elementos de simetria. Ele serve para mostrar que o símbolo se refere a um elemento de simetria e não, por exemplo, a uma operação de simetria. Se isto já estiver claro no contexto, então o E pode ser omitido, por exemplo ‘um eixo 2’ em vez de ‘um eixo E2’.

Tabela 1. Elementos geométricos de operações de simetria em grupos de pontos e grupos espaciais
Operação de simetria	Elemento geométrico	Parâmetros adicionais
Identidade	Não é necessário	Nenhum
Tradução	Não é necessário	Vector $\mathbf{t}$
Reflexão no plano A	Plano A	Nenhum
Reflexão no plano A e tradução $\mathbf{v}$ paralelo a A	Plano A	Vetor de deslizamento $\mathbf{v}$
Rotação sobre a linha b	Linha b	Angulo e sentido de rotação
Rotação do parafuso = rotação sobre a linha b e translação $\mathbf{u}$ paralelo a b	Linha b	Angulo e sentido de rotação do parafuso vetor $\mathbf{u}$
Rotoinversão = rotação sobre a linha b e inversão através do ponto P sobre b	Linha b e ponto P sobre b	Angulo (não igual a $\pi$ ) e sentido de rotação
Inversão através do ponto P	Ponto P	Nenhum

O símbolo Eg listado no Relatório de 1989 pode ser usado para planos de planeio se se quiser apenas mostrar que o elemento de simetria é um plano de planeio. Por outro lado, se ele pertence a um dos tipos especiais que há muito tempo foram denotados por uma letra apropriada (a, b, c, n ou d; cf. ITA83), então essa letra substitui g em Eg.

Tabela 2. Elementos de simetria em grupos de pontos e grupos espaciais
Nome do elemento de simetria	Símbolo	Elemento geométrico	Operação definidora (d.o.)	Operações no conjunto de elementos
Plano de espelho	Em	Plano A	Reflexão em A	D.o. e seus equivalentes coplanares*
Plano de deslizamento	Eg $\ddag$	Plano A	Reflexão do deslizamento em A, 2v (não v) uma tradução da malha	D.o. e seus equivalentes coplanares*
Eixo de rotação	En	Linha b	Rotação sobre b, ângulo $2\pi/n$ ,n = 2, 3, 4 ou 6	1º, $\dots$ ,(n – 1)as potências de d.o. e seus equivalentes coaxiais $\dag$
Eixo de parafuso	Enj	Linha b	Rotação de parafuso sobre b, ângulo $2\pi/n$ , u =j/n vezes menor malha tradução ao longo de b, parafuso direito; n = 2, 3, 4 ou 6,	1st, $\dots$ ,(n – 1)os poderes de d.o. e seus equivalentes coaxiais $\dag$
Eixo de rotação	$E\bar n$	Linha b e ponto P sobre b	Rotoinversão: rotação sobre b, ângulo $2\pi/n$ , e inversão através de P; n = 3, 4 ou 6	D.o. e sua inversão
Centro	$E\bar 1$	Ponto P	Inversão por P	D.o. apenas

* Ou seja, todas as reflexões de planeio com o mesmo plano de reflexão, com vectores de planeio diferentes do do d.o. (tomado como zero para uma reflexão) por um vector de translação da malha.
$\dag$ Quer dizer, todas as rotações e rotações de parafuso com o mesmo eixo b, o mesmo ângulo e sentido de rotação e o mesmo vector de parafuso $\mathbf{u}$ (zero para uma rotação) até um vector de translação da malha.
$\ddag$ Em Eg, g é substituído por a, b, c, n, d, e ou k para tipos específicos de planos de planeio, cf. §2.

Um novo e importante aspecto de símbolos como Eb pode, no entanto, ser apontado. De acordo com a ITA83, denotar um plano por b significa apenas que uma reflexão de planeio no plano com um componente de planeio b/2 ao longo do eixo b é uma operação de simetria. Esta definição certamente se aplica à situação descrita na Fig. 1.

Fig. 1. (Depois de W. Fischer.) O conjunto de elementos de um plano Eb-glide, mostrado como um conjunto de pontos acima (+) e abaixo (-) do plano produzido por reflexos de planeio no plano, partindo, por exemplo, do sinal + no canto superior esquerdo. A rede N de translações paralelas ao plano (+ $\cdots$ + vectores) é indicada por uma malha, que neste caso acontece ser rectangular. Ambos os pares de bordas são paralelos aos eixos cristalinos. Existe uma reflexão de planeio com o seu vector de planeio (+ $\cdots$ -) ao longo do eixo b.

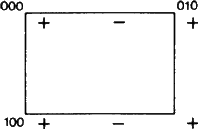
$\begin{figure} \incluindo gráficos. \Fim{figurar}$

Fig. 1 é adaptado, assim como as Figs. 2 e 3, a partir de um conjunto de figuras similares desenhadas pelo membro do Comitê Ad-hoc W. Fischer como um inventário de todos os tipos de planos de planeio. Embora o conjunto tenha sido apresentado ao Comitê em 1980, muito antes do Relatório de 1989, cada uma de suas figuras mostra precisamente o ‘conjunto de elementos’ do plano de planeio como definido naquele Relatório (cf. o resumo acima). Para um plano de planeio, o conjunto de elementos consiste em todos os reflexos de planeio tendo o plano como seu elemento geométrico comum. Sua ação é mostrada em projeção sobre este plano. A partir da posição inicial de qualquer sinal +, cada sinal – resulta de um dos reflexos de planeio do conjunto. Todos estes são mostrados dentro de uma malha elementar do padrão bidimensional periódico resultante de sinais + e -3837>

Referimo-nos frequentemente à rede N formada por todas as translações paralelas ao plano; esta rede é facilmente visualizada olhando apenas para sinais +. Estes vetores devem ser claramente distinguidos dos vetores que conectam um sinal + com qualquer – sinal, cada um dos quais é o vetor de um reflexo de planeio pertencente ao conjunto de elementos.

O novo aspecto surge porque, em alguns casos, pela definição da ITA83, o plano b-glide é também um plano a-glide; veja Fig. 2. Claramente isto só acontece se a rede N estiver centrada ortogonalmente, porque então o planeio pode ser transformado em planeio b (e vice versa) adicionando uma tradução centrada. A prática até agora tem sido chamar esse planeio arbitrariamente de a ou b, causando assim um enviesamento injustificado e uma falta de singularidade nesses símbolos. Portanto, propomos que o caso da Fig. 2 seja coberto por um símbolo separado.

Fig. 2. (Depois de W. Fischer.) O conjunto de elementos de um plano de Ee-glide. Cf. legenda da Fig. 1. Note que a rede N aqui é centrada ortogonalmente.

\begin{figure} \incluindo gráficos. \O alcance deste símbolo deve então ser estendido aos planos de planeio em diagonal, ou seja, paralelo a apenas um eixo de cristal, desde que o plano de planeio tenha um vector de planeio ao longo desse eixo e que a rede N esteja centrada ortogonalmente. Para tais planos não existe a ambiguidade da escolha aleatória a-b acima referida, mas o âmbito alargado do novo símbolo está de acordo com o de todos os símbolos existentes (nomeadamente a, b, c, n e d). Cada um destes é utilizado para um plano de planeio com um e dois eixos de cristal na rede N, cf. Fig. 3.

A letra e é proposta para o novo símbolo. Assim, Ee será aplicado para planos de planeio com redes ortogonais centradas N e pelo menos um vector de planeio ao longo de um eixo de cristal. Um novo critério é portanto necessário: nomeadamente a orientação dos vectores de planeio em relação aos eixos convencionais do cristal. Como estes últimos estão ao longo de direções simétricas, enquanto que cada plano de planeio é paralelo a um plano espelho da malha, não é surpreendente que haja sempre pelo menos um eixo de cristal convencional em N. Se existe apenas um desses eixos, então perpendicular a ele há sempre outra translação em N.

O novo símbolo e assim como os antigos símbolos a, b, c, d, n serão agora redefinidos em termos deste novo critério e do tipo de rede Bravais N. Esta rede é monoclínica ou ortogonal ou tetragonal primitiva (mp ou op ou tp) ou ortogonal centrada (oc). Apenas as redes do tipo oc N permitem um plano Ee-glide. O símbolo En é aplicável às redes N do tipo Bravais mp ou op, enquanto Ed é para redes do tipo oc N. (Como indicado em uma nota de rodapé da Tabela 1.3 no ITA83: ‘Planos de planeio d ocorrem apenas em grupos espaciais ortogonais F, em grupos espaciais tetragonais I e em grupos espaciais cúbicos I e F. Ocorrem sempre em pares com vetores de planeio alternado’). Em contraste com os planos Ea, Eb, Ec e Ee, no entanto, para os planos En e Ed não existe um vetor de planeio paralelo ou perpendicular a um eixo convencional em N.

As definições resultantes dos planos de planeio dos tipos acima estão resumidas nas linhas (i) e (ii) da Tabela 3, e mais explicitamente na Fig. 3.

Tabela 3. Símbolos impressos para tipos especiais de planos de planeio
Número de vectores de planeio paralelos ou perpendiculares aos eixos de cristal na rede N	Bravais tipo de rede N
O símbolo é determinado por dois critérios. Um critério é o tipo Bravais (mp, op, tp ou oc) da rede N formada pelas translações de simetria paralelas ao plano em consideração. Esta rede contém sempre pelo menos um eixo de cristal convencional.* O outro critério refere-se à orientação dos vectores de planeio em relação a esses eixos.
	m, op, tp	oc
(i) Um ou dois paralelos	Ec(Ea, Eb)	Ee
(ii) Nenhum paralelo, nenhum perpendicular	En	Ed
(iii) Nenhum paralelo, um perpendicular	Ek	–

* Conforme definido em ITA83, § 9.1; entretanto, para grupos espaciais romboédricos, apenas eixos hexagonais são utilizados aqui.

Todos os planos de planeio restantes estavam anteriormente sem símbolo específico. Cada um deles tem uma orientação diagonal (apenas um eixo de cristal convencional na rede N). Entre os reflexos de planeio no seu conjunto de elementos, não existe nenhum com um vector de planeio ao longo desse eixo. No entanto, um vetor de planeio é (por simetria) perpendicular a ele. Um símbolo parece desejável, então novamente uma nova letra é proposta: k. O novo símbolo Ek é brevemente definido na linha (iii) da Tabela 3 e é totalmente ilustrado no bloco inferior da Fig. 3. Alguns exemplos são dados em §2.

Fig. 3. (Adaptado dos desenhos de W. Fisher.) Todos os aspectos possíveis dos conjuntos de elementos dos planos de planeio mostrados como na Fig. 1, mas independentes das etiquetas dos eixos. Os diagramas estão agrupados em colunas encabeçadas pelo símbolo tipo rede Bravais (linha superior) das suas redes N, cf. Tabela 3. Os outros critérios dessa tabela são verificados olhando primeiro para as linhas duplas que mostram as direções dos eixos dos cristais no plano. Uma aresta (vertical) da malha de N mostrada é sempre escolhida ao longo de tal eixo. A outra aresta é horizontal, exceto em (1) e (8). Para os diagramas (1), $\dots$ ,(5), o símbolo do plano planador é a etiqueta a, b ou c do eixo vertical; para os outros é a letra circundada no bloco delineado que contém o diagrama. Observe os vetores de planeio vertical nos diagramas (1), $\dots$ ,(7), os horizontais em (6), (7), (14), (15) e a ausência de um ou outro em (8), $\dots$ ,(13). Um exemplo de ocorrência é dado abaixo de cada diagrama pelo símbolo do grupo de espaços e pelo trigêmeo de coordenadas do plano.

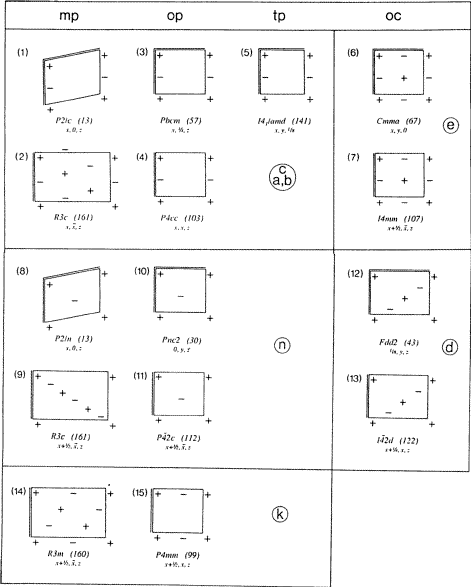
$\begin{figure} \incluindo gráficos. \{figurar}$

Na Fig. 3, o inventário de Fischer de todos os tipos de planos de planeio é mostrado de forma abreviada – embora ainda completa – na qual foi dada maior proeminência gráfica aos eixos de cristal. Para cada diagrama, um exemplo de sua ocorrência em um grupo espacial é listado.

Em alguns grupos espaciais romboedrais, os planos Ec, En e Ek diagonalmente orientados ocorrem com redes do tipo mp N que podem ser descritas através da centralização tripla de uma rede ortogonal. Uma malha tripla retangular da rede N é mostrada para estes tipos de planos de planeio na Fig. 3, diagramas (2), (9) e (14). No diagrama (9), a semelhança com outros n diagramas como (8) ou (10) é reconhecida se em (9) uma malha primitiva monoclínica da rede N for considerada com vetores de planeio diagonal.

Símbolos gráficos para elementos de simetria

Os símbolos gráficos existentes como definidos e utilizados no ITA83 são considerados adequados pelo Comitê Ad-hoc, com uma exceção. A situação é muito diferente da dos símbolos impressos porque nos desenhos a direção de projeção se torna um parâmetro adicionado. Nos termos ‘projeção perpendicular’ e ‘projeção paralela’ utilizados abaixo, perpendicular e paralela referem-se à orientação da direção de projeção em relação ao plano de planeio.

Para um plano Ee o símbolo 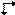existe para sua projeção perpendicular. Os símbolos gráficos existentes para a projecção paralela de um plano Ee-glide, no entanto, sofrem da mesma ambiguidade que os símbolos impressos. Eles expressam o vetor de planeio tanto paralelo como perpendicular à direção de projeção, mas a escolha é arbitrária. Portanto, um novo símbolo é proposto para a projecção paralela de um plano de planeio Ee, nomeadamente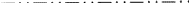

Exemplos de planos Ee.

Todos os planos de planeio paralelos a dois eixos nos grupos espaciais Fmm2, Fmmm, $Fm\bar 3$ , $Fm\bar 3m$ e $Fm\bar 3c$ (Nos. 42, 69, 202, 225 e 226), assim como certos planos nos cinco grupos espaciais listados em §3.

Os planos Ee de orientação diagonal ocorrem nos grupos espaciais I4mm, I4cm, $I\bar 42m$ , I4/mmm, I4/mcm, $I\bar 43m$ e $Im\bar 3m$ (Nos. 107, 108, 121, 139, 139, 140, 217 e 229).

No ITA83 todos estes planos Ee são desenhados arbitrariamente como linhas pontilhadas ou tracejadas em suas projeções paralelas. Fig. 4 mostra o diagrama do grupo espacial I4cm (No. 108), tanto como mostrado no ITA83 como com o uso do novo símbolo.

Fig. 4. (a) Diagrama do grupo de espaços I4cm (No. 108) retirado do ITA83. (b) O mesmo, modificado pelo uso do símbolo gráfico proposto no § 2, para a projeção paralela de um plano Ee.

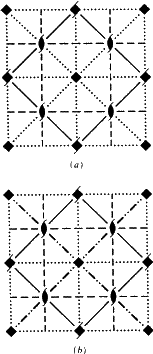
$\begin{figure} \incluindo gráficos. \{figurar}$

Embora Ek seja um novo símbolo de impressão, nos diagramas da ITA83 todos os planos de planeio Ek foram desenhados satisfatoriamente com as mesmas convenções utilizadas para os planos de planeio Ea/b/c. Como nesses casos, há um único vetor de planeio especial (perpendicular ao eixo do cristal na rede N, cf. tabela 3). Quando este vector é, por exemplo, paralelo ao plano de projecção, o plano Ek é sempre desenhado como a linha tracejada prescrita pela convenção relevante. Portanto, nenhum novo símbolo gráfico é proposto para planos de planeio Ek.

Exemplos de planos Ek.

Semelhantes planos são prontamente encontrados nos diagramas da ITA83 como planos paralelos a apenas um eixo e projetados como linhas tracejadas, por exemplo xxz em P4bm e $P\bar 42_1m$ (Nos. 100 e 113). Em particular, a Tabela 3 está exatamente em conformidade com a distinção mostrada entre os planos Ek e En. Veja, por exemplo, as linhas tracejadas e tracejadas para R3m e R3c (Nos. 160 e 161).

Símbolos do grupo espacial Hermann-Mauguin

Os caracteres que aparecem após a letra da malha no símbolo Hermann-Mauguin (HM) de um grupo espacial foram originalmente destinados a representar as operações geradoras do grupo. Por exemplo, b era um reflexo b-glide num plano orientado de acordo com sua posição no símbolo HM.

Na prática, os elementos de simetria populares, embora mal definidos, tomaram o lugar das operações. Assim, b passou a ser visto como um plano de planeio, Eb na nossa terminologia actual. Não há nenhum dano nessa reinterpretação, exceto quando a operação pertence a um plano de planeio Ee-glide. Se isto se aplica, por exemplo, à reflexão do b-glide acima, então existe um Ee, mas não um plano Eb-glide na orientação correspondente. Neste caso, o b torna-se um caráter muito enganador. Além disso, o viés (dado a b sobre a ou c) é tão perturbador como no caso dos símbolos de elementos de simetria tratados em §1.

Por isso, é proposto substituir essas letras enganosas a ou b por e nos cinco símbolos HM em que elas ocorrem:

Space group No.	>39	41	64	67	68
Símbolo no ITA83:	Abm2	Aba2	Cmca	Cmma	Ccca
Novo símbolo:	Aem2	Aea2	Cmce	Cmme	Ccce.

Uma outra vantagem dos novos símbolos propostos é que e – ao contrário de a ou b – é neutro e, portanto, não é alterado na permutação de eixos.

Símbolos impressos para operações de simetria

Um conjunto completo de símbolos impressos foi concebido por W. Fischer & E. Koch (ITA83, §11.2) e foi extensivamente aplicado nas seções Operações de Simetria das descrições do grupo de espaço.

Em resumo, cada símbolo consiste de até três partes. A primeira parte é um único caractere (às vezes com um índice) que descreve o tipo de operação. A(s) parte(s) seguinte(s) dá(m) os componentes de qualquer deslocamento ou vetor de translação relevante – sempre entre parênteses – e as coordenadas do elemento geométrico da operação, nessa ordem.

O Comitê Ad-hoc, após considerar este sistema, deseja introduzir duas modificações para as reflexões do planeio:

(i) ao invés do presente primeiro caractere (que pode ser a, b, c, n, d ou g), escreva sempre a letra g;

(ii) escreva sempre os componentes do planeio-vetor (entre parênteses) por extenso, em particular para as reflexões simples do planeio nos planos a-, b- ou c-glide onde anteriormente eram omitidos.

Regra (i) suprime informações sobre o tipo de plano de planeio ao qual a operação pertence. Muito frequentemente essa informação é irrelevante ou mesmo confusa. Para planos a/b/c a supressão pode destruir informações essenciais, mas a perda é restaurada pela regra (ii) como mostrado no exemplo abaixo.

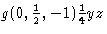Ao adotar estas mudanças, a uniformidade dos símbolos – também em relação aos de rotações – é muito melhorada. Por exemplo, o símbolo da reflexão do planeio no plano $x = \frac{1}{4}$ , com o invulgar vector de planeio $(0, \frac{1}{2}, -1)$ , a saber $g(0, \frac{1}{2}, 1) \frac{1}{4}yz$ , agora está alinhado com o de uma simples reflexão do planeio b-glide. No ITA83 este último foi denotado por $b \frac{1}{4} y z$ , mas isto é alterado pela regra (ii) em $g(0, \frac{1}{2}, 0) \frac{1}{4} y z$ .

As regras acima aplicam-se igualmente aos reflexos de planeio pertencentes ao conjunto de elementos de um plano espelho. Assim, se a componente de deslocamento de tal operação é (0, 1, 2), então seu símbolo começa com g(0, 1, 2), não com m(0, 1,2).

Tabelas Internacionais para Cristalografia (1983). Vol. A, editado por TH. HAHN, especialmente os §§ 1.1, 1.3, 1.4, 7 e 11. Dordrecht: Kluwer Academic Publishers.

International Tables for Crystallography (1989). Vol. A, 2nd, revisado, ed., ed., editado por TH. HAHN. Dordrecht: Kluwer Academic Publishers.

WOLFF, P. M. DE, BELOV, N. V., BERTAUT, E. F., BUERGER, M. J., DONNAY, J. D. H.., FISCHER, W., HAHN, TH., KOPTSIK, V. A., MACKAY, A. L., WONDRATSCHEK, H., WILSON, A. J. C. & ABRAHAMS, S. C. (1985). Acta Cryst. A41, 278-280.

WOLFF, P. M. DE, BILLIET, Y., DONNAY, J. D. H., FISCHER, W., GALIULIN, R. B., GLAZER, A. M., SENECHAL, M., SHOEMAKER, D. P., WONDRATSCHEK, H., HAHN, TH., WILSON, A. J. C. & ABRAHAMS, S. C. (1989). Acta Cryst. A45, 494-499.

…vectores. Os símbolos do planador c, n e k para os três diagramas (2), (9) e (14) da Fig. 3 foram atribuídos de acordo com a Tabela 3. Um membro do Comitê Ad-hoc (Professor Wondratschek) pensa que o símbolo n para diagrama (9) entra em conflito com noções tradicionais sobre n aviões. Ele propõe a atribuição de um símbolo especial para o diagrama (9). Esta proposta, porém, não recebeu o apoio adequado dentro do Comitê Ad-hoc.

Símbolos para elementos de simetria e operações de simetria