Neste artigo, vou explicar como as Convoluções 2D são implementadas como multiplicações de matrizes. Esta explicação é baseada nas notas do CS231n Convolutional Neural Networks for Visual Recognition (Módulo 2). Assumo que o leitor está familiarizado com o conceito de uma operação de convolução no contexto de uma rede neural profunda. Caso contrário, este repo tem um relatório e excelentes animações que explicam o que são convoluções. O código para reproduzir os cálculos deste artigo pode ser baixado aqui.
Pequeno Exemplo
Suponha que temos um único canal 4 x 4 imagem, X, e seus valores de pixel são os seguintes:
Outra suponha que definimos uma convolução 2D com as seguintes propriedades:

Isto significa que haverá 9 patches de imagem 2 x 2 que serão multiplicados por elementos com a matriz W, assim

Estes patches de imagem podem ser representados como vetores de coluna 4-dimensional e concatenados para formar uma única matriz 4 x 9, P, assim:

Note que a i-ésima coluna da matriz P é na verdade a i-ésima correção de imagem em forma de coluna vetorial.
A matriz de pesos para a camada de convolução, W, pode ser achatada para um vetor de linha 4-dimensional, K, como tal:
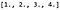
>
Para realizar a convolução, primeiro multiplicamos a matriz K por P para obter um vector de linha 9-dimensional (matriz 1 x 9) que nos dá:

Então reformulamos o resultado de K P para a forma correta, que é uma matriz 3 x 3 x 1 (última dimensão de canal). A dimensão do canal é 1 porque ajustamos os filtros de saída para 1. A altura e largura é 3 porque de acordo com as notas CS231n:

Isso significa que o resultado da convolução é o mesmo:
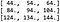
Que verifica se executamos a convolução usando funções PyTorch embutidas (veja este artigo acompanhando o código para detalhes).
Exemplo maior
O exemplo na secção anterior assume uma única imagem e os canais de saída da convolução é 1. O que mudaria se nós relaxássemos estas suposições?
Vamos assumir que a nossa entrada para a convolução é uma imagem 4 x 4 com 3 canais com os seguintes valores de pixel:
Como para a nossa convolução, vamos defini-la para ter as mesmas propriedades da secção anterior, excepto que os seus filtros de saída são 2. Isto significa que a matriz de pesos iniciais, W, deve ter forma (2, 2, 2, 3) i.e. (filtros de saída, altura do kernel, largura do kernel, canais da imagem de entrada). Vamos definir W para ter os seguintes valores:

Notem que cada filtro de saída terá o seu próprio kernel (razão pela qual temos 2 kernels neste exemplo) e cada canal do kernel é 3 (uma vez que a imagem de entrada tem 3 canais).
Desde que ainda estamos a girar um kernel 2 x 2 numa imagem 4 x 4 com 0 zero-padding e stride 1, o número de patches de imagem é ainda 9. No entanto, a matriz de patches de imagem, P, será diferente. Mais especificamente, a i-ésima coluna de P será a concatenação dos valores do 1º, 2º e 3º canais (como um vetor de coluna) correspondente ao patch de imagem i. P será agora uma matriz de 12 x 9. As linhas são 12 porque cada patch de imagem tem 3 canais e cada canal tem 4 elementos desde que definimos o tamanho do kernel para 2 x 2. Aqui está o aspecto de P:

As para W, cada kernel será achatado em um vetor de linha e concatenado em linha para formar uma matriz de 2 x 12, K. A i-ésima linha de K é a concatenação dos valores do 1º, 2º e 3º canal (em forma de linha vetorial) correspondente ao i-ésimo kernel. Aqui está como K será:


E aqui está o resultado depois de reformulá-lo para uma matriz 3 x 3 x 2:

Que novamente verifica se devemos fazer a convolução usando as funções PyTorch embutidas (veja o código que acompanha este artigo para detalhes).
Então o quê?
Por que devemos nos preocupar em expressar convoluções 2D em termos de multiplicações de matrizes? Além de ter uma implementação eficiente adequada para rodar em uma GPU, o conhecimento desta abordagem nos permitirá raciocinar sobre o comportamento de uma rede neural convolucional profunda. Por exemplo, He et. al. (2015) expressou convoluções 2D em termos de multiplicações de matrizes que lhes permitiram aplicar as propriedades de matrizes/vetores aleatórios para argumentar por uma melhor rotina de inicialização de pesos.
Conclusão
Neste artigo, expliquei como realizar convoluções 2D usando multiplicações de matrizes, passando por dois pequenos exemplos. Espero que isto seja suficiente para que você generalize para dimensões de imagem de entrada arbitrárias e propriedades de convolução. Deixe-me saber nos comentários se algo não estiver claro.
1D Convolution
O método descrito neste artigo também generaliza para convoluções 1D.
Por exemplo, suponha que sua entrada seja um vetor 12-dimensional de 3 canais assim:

Se definirmos nossa convolução 1D para ter os seguintes parâmetros:
- tamanho do núcleo: 1 x 4
- canais de saída: 2
- tride: 2
- padding: 0
- bias: 0
Então os parâmetros na operação de convolução, W, serão um tensor com forma (2 , 3, 1, 4). Vamos definir W para ter os seguintes valores:

Baseado nos parâmetros da operação de convolução, a matriz de “image” patches P, terá uma forma (12, 5) (5 patches de imagem onde cada patch de imagem é um vetor 12-D já que um patch tem 4 elementos em 3 canais) e terá este aspecto:
Próximo, achatamos W para obter K, que tem forma (2, 12) já que há 2 kernels e cada kernel tem 12 elementos. Este é o aspecto de K:
Agora podemos multiplicar K com P que dá:

Finalmente, remodelamos o K P para a forma correta, que de acordo com a fórmula é uma “imagem” com forma (1, 5). Isto significa que o resultado desta convolução é um tensor com forma (2, 1, 5), uma vez que definimos os canais de saída para 2. Este é o resultado final:

Que, como esperado, verifica se vamos executar a convolução usando as funções internas do PyTorch.