(IUCr) Símbolos de elementos de simetría

Acta Cryst. (1992). A48, 727-732

Informe final del Comité Ad-Hoc de la Unión Internacional de Cristalografía sobre la nomenclatura de la simetría*

Por P. M. DE WOLFF (Presidente), Meermanstraat 126, 2614 AM Delft, Países Bajos,

Y. BILLIET, Ecole Nationale d’Ingénieurs, BPW 3038 Sfax, Tunesië,

J. D. H. DONNAY, Department of Geological Sciences, McGill University, 3450 University Street, Montreal, Canada H3A 2A7,

W. FISCHER, Institut für Mineralogie, Petrologie und Kristallographie der Phillips-Universität, Lahnberge, D-3550 Marburg (Lahn), Alemania,

R. B. GALIULIN, Instituto de Cristalografía, Academia de Ciencias de Rusia, Leninsky Prospekt 59, Moscú 117333, Rusia,

A. M. GLAZER, Clarendon Laboratory, University of Oxford, Parks Road, Oxford OX1 3PU England,

TH. HAHN, Institut für Kristallographie, RWTH, Templergraben 55, D-5100 Aachen, Alemania,

MARJORIE SENECHAL, Department of Mathematics, Smith College, Northampton, MA 01063, USA,

D. P. SHOEMAKER, Chemistry Department, Oregon State University, OR 97331, USA,

H. WONDRATSCHEK, Institut für Kristallographie, Universität Karlsruhe, Kaiserstrasse 12, D-7500 Karlsruhe 1, Alemania,

A. J. C. WILSON (ex officio, IUCr Commission on International Tables), Crystallographic Data Centre, University Chemistry Laboratory, Lensfield Road, Cambridge CB2 1EW, England

Y S. C. ABRAHAMS (ex officio, IUCr Commission on Crystallographic Nomenclature), Department of Physics, Southern Oregon State College, 1250 Siskiyou Boulevard, Ashland, OR 97520-5047, USA

(Recibido el 7 de noviembre de 1991; aceptado el 9 de marzo de 1992)

* Nombrado el 14 de noviembre de 1984, modificado el 10 de agosto de 1987 según las reglas básicas indicadas en Acta Cryst. (1979), A35, 1072. Informe final aceptado el 23 de diciembre de 1991 por la Comisión de Nomenclatura Cristalográfica de la IUCr y el 9 de marzo de 1992 por el Comité Ejecutivo.

Abstract

Se proponen símbolos impresos nuevos o redefinidos a la luz de la redefinición recientemente aceptada de los elementos de simetría . En particular, la letra e abarca ciertos planos de deslizamiento que hasta ahora no tenían un símbolo único, como los llamados «o a o b». Se recomienda el uso de e en el símbolo de Hermann-Mauguin de cinco grupos espaciales diferentes. Para los planos e proyectados en una dirección paralela al plano, se propone un símbolo gráfico que elimina la ambigüedad de su designación actual. Se propone la letra k para una clase recién definida de planos de deslizamiento que hasta ahora carecían de símbolo específico. Los símbolos para las operaciones de simetría introducidos en las descripciones de los grupos espaciales de International Tables for Crystallography (1989), Vol. A (Dordrecht: Kluwer Academic Publishers) se recomiendan para su uso general, con modificaciones sólo para las operaciones de reflexión de deslizamiento.

Introducción

El Comité Ad-hoc designado en 1980 para considerar «los problemas de nomenclatura relativos a las operaciones de simetría y a los elementos de simetría en los grupos espaciales» ha publicado dos informes titulados Nomenclatura para familias de cristales, tipos de Bravais-Lattice y clases aritméticas (de Wolff et al., 1985) y Definition of Symmetry Elements in Space Groups and Point Groups (de Wolff et al., 1989). Como se señala en el Informe de 1989, el único problema pendiente en relación con las operaciones de simetría es el de la elección de los símbolos adecuados, ya que el concepto es claro. Se ha adoptado una notación provisional en las Tablas Internacionales de Cristalografía (1983, 1989), denominada en adelante ITA83.

Símbolos impresos para los elementos de simetría

La definición de los elementos de simetría que figura en el Informe de 1989 (de Wolff et al.) se utilizará a lo largo del presente Informe. Aquí repetimos la esencia:

Para cualquier operación de simetría dada se define su elemento geométrico (plano, punto y/o línea). Un elemento de simetría es la combinación del elemento geométrico de una de las operaciones de simetría en un grupo espacial dado con el conjunto (llamado `conjunto de elementos’) de todas las operaciones de simetría en ese grupo espacial que comparten este elemento geométrico.

Las definiciones explícitas de los elementos geométricos y las descripciones de los elementos de simetría resultantes, así como sus símbolos, se dan en las Tablas 1 y 2. (Son idénticas a las Tablas 1 y 2 del Informe de 1989, excepto para los planos de deslizamiento, y se repiten aquí para completarlas, véase más adelante). Cada elemento de simetría está representado por un símbolo formado por dos caracteres. El primer carácter es una E mayúscula para todos los elementos de simetría. Sirve para mostrar que el símbolo se refiere a un elemento de simetría y no, por ejemplo, a una operación de simetría. Si esto ya está claro por el contexto, se puede omitir la E, por ejemplo, «un eje 2» en lugar de «un eje E2».

Tabla 1. Elementos geométricos de las operaciones de simetría en grupos de puntos y grupos espaciales
Operación de simetría	Elemento geométrico	Parámetros adicionales
Identidad	No se requiere	Ninguna
Traducción	No se requiere	Vector $\mathbf{t}$
Reflexión en el plano A	Plano A	Ninguna
Reflexión en el plano A y traslación $\mathbf{v}$ paralela a A	Plano A	Vector de deslizamiento $\mathbf{v}$
Rotación sobre la línea b	Línea b	Ángulo y sentido de giro
Giro sobre la línea b y traslación $\mathbf{u}$ paralela a b	Línea b	Ángulo y sentido del tornillo de rotación vector $\mathbf{u}$
Rotoinversión = rotación sobre la línea b e inversión a través del punto P en b	Línea b y punto P en b	Ángulo (no igual a $\pi$ ) y sentido de giro
Inversión a través del punto P	Punto P	Nada

El símbolo Eg que figura en el Informe de 1989 puede utilizarse para los planos de deslizamiento si sólo se quiere demostrar que el elemento de simetría es un plano de deslizamiento. En cambio, si pertenece a uno de los tipos especiales que desde hace tiempo se denotan con una letra apropiada (a, b, c, n o d; cf. ITA83), entonces esa letra sustituye a g en Eg.

Tabla 2. Elementos de simetría en grupos puntuales y grupos espaciales
Nombre del elemento de simetría	Símbolo	Elemento geométrico	Operación definitoria (d.o.)	Operaciones en el conjunto de elementos
Plano espejo	Em	Plano A	Reflexión en A	D.o. y sus equivalentes coplanares*
Plano de deslizamiento	Eg $\ddag$	Plano A	Reflexión de deslizamiento en A, 2v (no v) una traslación de red	D.o. y sus equivalentes coplanares*
Eje de rotación	En	Línea b	Rotación alrededor de b, ángulo $2\pi/n$ ,n = 2, 3, 4 o 6	1ª, $\dots$ ,(n – 1)ª potencias del d.o. y sus equivalentes coaxiales $\dag$
Eje del tornillo	Enj	Línea b	Giro del tornillo en torno a b, ángulo $2\pi/n$ , u =j/n veces la traslación más corta de la red a lo largo de b, tornillo derecho; n = 2, 3, 4 ó 6, $j=1,\dots,(n-1)$	1ª, $\dots$ ,(n – 1)ª potencia de d.o. y sus equivalentes coaxiales $\dag$
Eje de rotación	$E\bar n$	Línea b y punto P en b	Rotoinversión: rotación alrededor de b, ángulo $2\pi/n$ , e inversión a través de P; n = 3, 4 ó 6	D.o. y su inversa
Centro	$E\bar 1$	Punto P	Inversión a través de P	D.o. sólo

* Es decir, todas las reflexiones de deslizamiento con el mismo plano de reflexión, con vectores de deslizamiento que difieren del del d.o. (tomado como cero para una reflexión) por un vector de traslación de la red.
$\dag$ Es decir, todas las rotaciones y rotaciones de tornillo con el mismo eje b, el mismo ángulo y sentido de rotación y el mismo vector de tornillo $\mathbf{u}$ (cero para una rotación) hasta un vector de traslación de la red.
$\ddag$ En Eg, g se sustituye por a, b, c, n, d, e o k para tipos específicos de planos de deslizamiento, cf. §2.

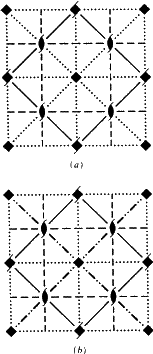
Sin embargo, puede señalarse un nuevo aspecto importante de símbolos como Eb. Según ITA83, denotar un plano por b significaba simplemente que una reflexión de deslizamiento en el plano con una componente de deslizamiento b/2 a lo largo del eje b es una operación de simetría. Esta definición se aplica ciertamente a la situación representada en la Fig. 1.

Fig. 1. (Según W. Fischer.) El conjunto de elementos de un plano de deslizamiento Eb, mostrado como un conjunto de puntos por encima (+) y por debajo (-) del plano producidos por las reflexiones de deslizamiento en el plano, empezando por ejemplo por el signo + en la parte superior izquierda. La red N de traslaciones paralelas al plano (vectores + $\cdots$ +) se indica mediante una malla, que en este caso resulta ser rectangular. Ambos pares de aristas son paralelas a los ejes del cristal. Hay una reflexión de deslizamiento con su vector de deslizamiento (+ $\cdots$ -) a lo largo del eje b.

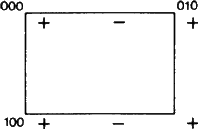
$\begin{figure} |includegraphics {fig1.ps}$

La Fig. 1 está adaptada, al igual que las Figs. 2 y 3, de un conjunto de figuras similares diseñadas por el miembro del Comité Ad-hoc W. Fischer como inventario de todos los tipos de planos de planeo. Aunque el conjunto fue presentado al Comité en 1980, mucho antes de que se publicara el Informe de 1989, cada una de sus figuras muestra precisamente el «conjunto de elementos» del plano de planeo tal como se define en dicho Informe (véase el resumen anterior). Para un plano de planeo, el conjunto de elementos está formado por todas las reflexiones de planeo que tienen el plano como elemento geométrico común. Su acción se muestra en proyección sobre este plano. Desde la posición inicial de cualquier signo +, cada signo – resulta de una de las reflexiones de deslizamiento del conjunto. Todos ellos se muestran dentro de una malla elemental del patrón periódico bidimensional resultante de signos + y -.

A menudo nos referiremos a la red N formada por todas las traslaciones paralelas al plano; esta red se visualiza fácilmente observando sólo los signos +. Estos vectores deben distinguirse claramente de los vectores que conectan un signo + con cualquier signo -, cada uno de los cuales es el vector de deslizamiento de una reflexión de deslizamiento perteneciente al conjunto de elementos.

El nuevo aspecto surge porque, en algunos casos, por la definición de ITA83, el plano de deslizamiento b es también un plano de deslizamiento a; véase la Fig. 2. Evidentemente, esto sólo ocurre si la red N está centrada ortogonalmente, porque entonces el deslizamiento a puede convertirse en un deslizamiento b (y viceversa) añadiendo una traslación de centrado. Hasta ahora, la práctica ha consistido en llamar arbitrariamente a un plano de deslizamiento de este tipo, ya sea a o b, provocando así un sesgo injustificado y una falta de unicidad en estos símbolos. Por lo tanto, proponemos que el caso de la Fig. 2 sea cubierto por un símbolo separado.

Fig. 2. (Según W. Fischer.) El conjunto de elementos de un plano Ee-glide. Cf. leyenda de la Fig. 1. Nótese que aquí la red N está centrada ortogonalmente.

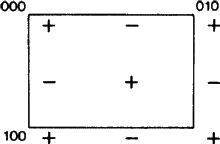
$\begin{figure} |includegraphics {fig2.ps}$

El alcance de este símbolo debe extenderse a los planos de deslizamiento con orientación diagonal, es decir, paralelos a un solo eje del cristal, siempre que el plano de deslizamiento tenga un vector de deslizamiento a lo largo de ese eje y que la red N esté centrada ortogonalmente. Para estos planos no existe la ambigüedad de la elección aleatoria a-b anterior, pero el alcance ampliado del nuevo símbolo coincide con el de todos los símbolos existentes (a, b, c, n y d). Cada uno de ellos se utiliza para un plano de deslizamiento con uno y dos ejes de cristal en la red N, cf. Fig. 3.

Se propone la letra e para el nuevo símbolo. Así, Ee se aplicará a los planos de deslizamiento con redes centradas ortogonales N y al menos un vector de deslizamiento a lo largo de un eje de cristal. Por lo tanto, es necesario un nuevo criterio: la orientación de los vectores de deslizamiento con respecto a los ejes convencionales del cristal. Dado que estos últimos se encuentran a lo largo de las direcciones de simetría, mientras que cada plano de deslizamiento es paralelo a un plano espejo de la red, no es sorprendente que siempre haya al menos un eje convencional del cristal en N. Si sólo hay un eje de este tipo, entonces perpendicular a él siempre hay otra traslación en N.

El nuevo símbolo e así como los antiguos símbolos a, b, c, d, n se redefinirán ahora en términos de este nuevo criterio y del tipo de red N de Bravais. Esta red es monoclínica u ortogonal o tetragonal primitiva (mp u op o tp) u ortogonal centrada (oc). Sólo las redes N de tipo oc permiten un plano de deslizamiento Ee. El símbolo En es aplicable a las redes N de tipo Bravais mp u op, mientras que Ed lo es para las redes N de tipo oc. (Como se indica en una nota a pie de página de la tabla 1.3 en ITA83: «Los planos de deslizamiento d se dan sólo en los grupos espaciales ortorrómbicos F, en los grupos espaciales tetragonales I y en los cúbicos I y F. Siempre se presentan en pares con vectores de deslizamiento alternados»). Sin embargo, a diferencia de los planos Ea, Eb, Ec y Ee, para los planos En y Ed no hay ningún vector de deslizamiento ni paralelo ni perpendicular a un eje convencional en N.

Las siguientes definiciones de los planos de deslizamiento de los tipos anteriores se resumen en las líneas (i) y (ii) de la Tabla 3, y más explícitamente en la Fig. 3.

Tabla 3. Símbolos impresos para tipos especiales de planos de planeo
Número de vectores de deslizamiento paralelos o perpendiculares a los ejes del cristal en la red N	Tipo de red Bravais N
El símbolo se determina por dos criterios. Un criterio es el tipo de Bravais (mp, op, tp u oc) de la red N formada por las traslaciones de simetría paralelas al plano considerado. Esta red siempre contiene al menos un eje cristalino convencional.* El otro criterio se refiere a la orientación de los vectores de deslizamiento con respecto a dichos ejes.
	m, op, tp	oc
(i) Uno o dos paralelos	Ec(Ea, Eb)	Ee
(ii) Ninguna paralela, ninguna perpendicular	En	Ed
(iii) Ninguna paralela, una perpendicular	Ek	–

* Como se define en ITA83, § 9.1; sin embargo, para los grupos espaciales romboédricos, aquí sólo se utilizan los ejes hexagonales.

Todos los planos de deslizamiento restantes estaban antes sin símbolo específico. Cada uno de ellos tiene una orientación diagonal (sólo un eje de cristal convencional en la red N). Entre los reflejos de deslizamiento en su conjunto de elementos, no hay ninguno con un vector de deslizamiento a lo largo de ese eje. Sin embargo, un vector de deslizamiento es (por simetría) perpendicular a él. Parece deseable un símbolo, así que de nuevo se propone una nueva letra: k. El nuevo símbolo Ek se define brevemente en la línea (iii) de la Tabla 3 y se ilustra completamente en el bloque inferior de la Fig. 3. En §2 se dan algunos ejemplos.

Fig. 3. (Adaptada de los dibujos de W. Fisher.) Todos los aspectos posibles de los conjuntos de elementos de los planos de deslizamiento mostrados como en la Fig. 1, pero independientes de las etiquetas de los ejes. Los diagramas se agrupan en columnas encabezadas por el símbolo del tipo de red Bravais (línea superior) de sus redes N, cf. Tabla 3. Los demás criterios de dicha tabla se verifican observando primero las líneas dobles que muestran las direcciones de los ejes de los cristales en el plano. Un borde (vertical) de la malla de N mostrada se elige siempre a lo largo de dicho eje. El otro borde es horizontal, excepto en (1) y (8). Para los diagramas (1), $\dots$ ,(5), el símbolo del plano de deslizamiento es la etiqueta a, b o c del eje vertical; para los demás es la letra encerrada en el bloque perfilado que contiene el diagrama. Observe los vectores de deslizamiento verticales en los diagramas (1), $\dots$ ,(7), los horizontales en (6), (7), (14), (15) y la ausencia de cualquiera de ellos en (8), $\dots$ ,(13). Un ejemplo de ocurrencia se da debajo de cada diagrama por el símbolo del grupo espacial y el triplete de coordenadas del plano.

\begin{figure} \N – Incluir gráficos {fig3.ps} \En la Fig. 3, el inventario de Fischer de todos los tipos de planos de deslizamiento se muestra de forma abreviada -aunque todavía completa- en la que se ha dado más protagonismo gráfico a los ejes de los cristales. Para cada diagrama, se enumera un ejemplo de su ocurrencia en un grupo espacial.

En algunos grupos espaciales romboédricos, los planos Ec, En y Ek orientados diagonalmente ocurren con redes de tipo mp N que pueden describirse mediante el triple centrado de una red ortogonal. Una malla triple rectangular de la red N se muestra para estos tipos de planos de deslizamiento en la Fig. 3, diagramas (2), (9) y (14). En el diagrama (9) se reconoce la similitud con otros diagramas n como el (8) o el (10) si en el (9) se considera una malla primitiva monoclínica de la red N con vectores de deslizamiento diagonales.

Símbolos gráficos para los elementos de simetría

Los símbolos gráficos existentes, tal y como se definieron y utilizaron en ITA83, son considerados adecuados por el Comité Ad-hoc con una excepción. La situación es muy diferente a la de los símbolos impresos porque en los dibujos la dirección de proyección se convierte en un parámetro añadido. En los términos `proyección perpendicular’ y `proyección paralela’ utilizados a continuación, perpendicular y paralelo se refieren a la orientación de la dirección de proyección con respecto al plano de planeo.

Para un plano Ee existe el símbolo 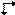para su proyección perpendicular. Los símbolos gráficos existentes para la proyección paralela de un plano de deslizamiento Ee, sin embargo, sufren de la misma ambigüedad que los símbolos impresos. Expresan el vector de deslizamiento de forma paralela o perpendicular a la dirección de proyección, pero la elección es arbitraria. Por lo tanto, se propone un nuevo símbolo para la proyección paralela de un plano de deslizamiento Ee, a saber

Ejemplos de planos Ee.

Todos los planos de deslizamiento paralelos a dos ejes en los grupos espaciales Fmm2, Fmmm, $Fm\bar 3$ , $Fm\bar 3m$ y $Fm\bar 3c$ (números 42, 69, 202, 225 y 226), así como ciertos planos en los cinco grupos espaciales enumerados en §3.

Los planos Ee orientados diagonalmente aparecen en los grupos espaciales I4mm, I4cm, $I\bar 42m$ , I4/mmm, I4/mcm, $I\bar 43m$ y $Im\bar 3m$ (Nos. 107, 108, 121, 139, 140, 217 y 229).

En ITA83 todos estos planos Ee están dibujados de forma bastante arbitraria como líneas punteadas o discontinuas en sus proyecciones paralelas. La Fig. 4 muestra el diagrama del grupo espacial I4cm (nº 108), tanto como se muestra en ITA83 como con el uso del nuevo símbolo.

Fig. 4. (a) Diagrama del grupo espacial I4cm (nº 108) tomado de ITA83. (b) Lo mismo, modificado utilizando el símbolo gráfico propuesto en § 2, para la proyección paralela de un plano Ee.

$\begin{figure} |includegraphics {fig4.ps} \end{figure}$

Aunque Ek es un nuevo símbolo de impresión, en los diagramas de ITA83 todos los planos de planeo Ek se han dibujado satisfactoriamente con las mismas convenciones utilizadas para los planos de planeo Ea/b/c. Como en estos casos, existe un único vector de deslizamiento especial (perpendicular al eje del cristal en la red N, cf. Tabla 3). Cuando este vector es, por ejemplo, paralelo al plano de proyección, el plano Ek se dibuja siempre como la línea discontinua prescrita por la convención correspondiente. Por lo tanto, no se propone ningún símbolo gráfico nuevo para los planos de deslizamiento Ek.

Ejemplos de planos Ek.

Tales planos se encuentran fácilmente en los diagramas de ITA83 como planos paralelos a un solo eje y proyectados como líneas discontinuas, por ejemplo, xxz en P4bm y $P\bar 42_1m$ (números 100 y 113). En particular, la tabla 3 se ajusta exactamente a la distinción mostrada entre los planos Ek y En. Véanse, por ejemplo, las líneas discontinuas y punteadas para R3m y R3c (números 160 y 161).

Símbolos de grupos espaciales de Hermann-Mauguin

Los caracteres que aparecen después de la letra de red en el símbolo de Hermann-Mauguin (HM) de un grupo espacial estaban destinados originalmente a representar operaciones generadoras del grupo. Por ejemplo, b era una reflexión b-glide en un plano orientado según su posición en el símbolo HM.

En la práctica, los populares aunque mal definidos elementos de simetría tomaron el relevo de las operaciones. Así, b pasó a verse como un plano de deslizamiento, Eb en nuestra terminología actual. Esta reinterpretación no tiene nada de malo, excepto cuando la operación pertenece a un plano de deslizamiento Ee. Si esto es así, por ejemplo, para la reflexión b-glide anterior, entonces hay un plano Ee pero no Eb-glide en la orientación correspondiente. En este caso, b se convierte en un carácter muy engañoso. Aparte de esto, el sesgo (dado a b sobre a o c) es tan perturbador como en el caso de los símbolos de elementos de simetría tratados en §1.

Por lo tanto, se propone sustituir tales letras engañosas a o b por e en todos los cinco símbolos HM en los que aparecen:

Grupo espacial No.	39	41	64	67	68
Símbolo en ITA83:	Abm2	Aba2	Cmca	Cmma	Ccca
Nuevo símbolo:	Aem2	Aea2	Cmce	Cmme	Ccce.

Una ventaja más de los nuevos símbolos propuestos es que e -a diferencia de a o b- es neutro y, por tanto, no se modifica al permutar el eje.

Símbolos impresos para operaciones de simetría

Un conjunto completo de símbolos impresos fue diseñado por W. Fischer & E. Koch (ITA83, §11.2) y se aplicó ampliamente en las secciones de Operaciones de Simetría de las descripciones de los grupos espaciales.

En resumen, cada símbolo consta de hasta tres partes. La primera parte es un solo carácter (a veces con un índice) que describe el tipo de operación. La(s) parte(s) siguiente(s) da(n) los componentes de cualquier vector de desplazamiento o traslación relevante – siempre entre paréntesis – y las coordenadas del elemento geométrico de la operación, en ese orden.

El Comité Ad-hoc, tras considerar este sistema, desea introducir dos modificaciones para las reflexiones de deslizamiento:

(i) en lugar del actual primer carácter (que puede ser a, b, c, n, d o g), escribir siempre la letra g;

(ii) escribir siempre las componentes del vector de deslizamiento (entre paréntesis) en su totalidad, en particular para las reflexiones de deslizamiento simples en los planos de deslizamiento a, b o c, donde antes se omitían.

La regla (i) suprime la información sobre el tipo de plano de deslizamiento al que pertenece la operación. Muy a menudo esa información es irrelevante o incluso confusa. Para los planos a/b/c la supresión puede destruir información esencial, pero la pérdida se restablece con la regla (ii), como se muestra en el ejemplo siguiente.

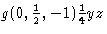Al adoptar estos cambios, la uniformidad de los símbolos -también con respecto a los de las rotaciones- mejora mucho. Por ejemplo, el símbolo de la reflexión de deslizamiento en el plano $x = \frac{1}{4}$ , con el inusual vector de deslizamiento $(0, \frac{1}{2}, -1)$ , es decir, $g(0, \frac{1}{2}, 1) \frac{1}{4}yz$ , coincide ahora con el de una reflexión de deslizamiento b simple. En ITA83, esta última se denominaba $b \frac{1}{4} y z$ , pero la regla (ii) la convierte en $g(0, \frac{1}{2}, 0) \frac{1}{4} y z$ .

Las reglas anteriores se aplican igualmente a las reflexiones de deslizamiento que pertenecen al conjunto de elementos de un plano espejo. Así, si la componente de desplazamiento de tal operación es (0, 1, 2), entonces su símbolo comienza con g(0, 1, 2), no con m(0, 1,2).

Tablas Internacionales de Cristalografía (1983). Vol. A, editado por TH. HAHN, especialmente los §§ 1.1, 1.3, 1.4, 7 y 11. Dordrecht: Kluwer Academic Publishers.

Tablas Internacionales de Cristalografía (1989). Vol. A, 2nd, revised, ed., edited by TH. HAHN. Dordrecht: Kluwer Academic Publishers.

WOLFF, P. M. DE, BELOV, N. V., BERTAUT, E. F., BUERGER, M. J., DONNAY, J. D. H., FISCHER, W., HAHN, TH., KOPTSIK, V. A., MACKAY, A. L., WONDRATSCHEK, H., WILSON, A. J. C. & ABRAHAMS, S. C. (1985). Acta Cryst. A41, 278-280.

WOLFF, P. M. DE, BILLIET, Y., DONNAY, J. D. H., FISCHER, W., GALIULIN, R. B., GLAZER, A. M., SENECHAL, M., SHOEMAKER, D. P., WONDRATSCHEK, H., HAHN, TH., WILSON, A. J. C. & ABRAHAMS, S. C. (1989). Acta Cryst. A45, 494-499.

…vectores. Los símbolos del plano de deslizamiento c, n y k para los tres diagramas (2), (9) y (14) de la Fig. 3 se han asignado, por supuesto, según la Tabla 3. Un miembro del Comité Ad-hoc (el profesor Wondratschek) opina que el símbolo n para el diagrama (9) entra en conflicto con las nociones tradicionales sobre los n planos. Propone que se asigne un símbolo especial al diagrama (9). Sin embargo, esta propuesta no ha recibido suficiente apoyo en el Comité Ad-hoc.

Símbolos de elementos de simetría y operaciones de simetría