Während die Methoden des vorangegangenen Abschnitts für die Beschreibung und Darstellung von Stichprobendaten nützlich sind, zeigt sich die wahre Stärke der Statistik, wenn wir Stichproben verwenden, um Informationen über Populationen zu erhalten. In diesem Zusammenhang ist eine Grundgesamtheit die gesamte Sammlung von Objekten von Interesse, z. B. die Verkaufspreise für alle Einfamilienhäuser auf dem Wohnungsmarkt, die in unserem Datensatz enthalten sind. Wir würden gerne mehr über diese Grundgesamtheit erfahren, um eine Entscheidung über den Kauf eines Hauses treffen zu können, aber die einzigen Daten, die uns zur Verfügung stehen, sind eine Zufallsstichprobe von 30 Verkaufspreisen.

Dennoch können wir „statistisches Denken“ anwenden, um durch die Analyse der Stichprobendaten Rückschlüsse auf die Grundgesamtheit zu ziehen. Insbesondere verwenden wir den Begriff des Modells – eine mathematische Abstraktion der realen Welt -, das wir an die Stichprobendaten anpassen. Wenn dieses Modell eine angemessene Anpassung an die Daten bietet, d. h. wenn es die Art und Weise, in der die Daten variieren, annähern kann, dann gehen wir davon aus, dass es auch das Verhalten der Grundgesamtheit annähern kann. Das Modell bildet dann die Grundlage für Entscheidungen über die Grundgesamtheit, indem es beispielsweise Muster aufzeigt, Schwankungen erklärt und zukünftige Werte vorhersagt. Dieser Prozess kann natürlich nur funktionieren, wenn die Stichprobendaten als repräsentativ für die Grundgesamtheit angesehen werden können.

Selbst wenn wir wissen, dass eine Stichprobe nicht zufällig ausgewählt wurde, können wir sie manchmal modellieren. In diesem Fall ist es zwar nicht möglich, aus der Stichprobe formale Rückschlüsse auf die Grundgesamtheit zu ziehen, aber die der Stichprobe zugrunde liegende Struktur kann dennoch modelliert werden. Ein Beispiel wäre eine Zufallsstichprobe – eine Stichprobe, die eher aus Gründen der Zweckmäßigkeit als wegen ihrer statistischen Eigenschaften ausgewählt wurde. Bei der Modellierung solcher Stichproben sollten alle Ergebnisse mit der Warnung versehen werden, dass die Schlussfolgerungen auf Objekte beschränkt werden sollten, die denen der Stichprobe ähnlich sind. Eine andere Art von Beispiel ist, wenn die Stichprobe die gesamte Population umfasst. So könnte man beispielsweise Daten für alle 50 Bundesstaaten der Vereinigten Staaten von Amerika modellieren, um etwaige Muster oder systematische Zusammenhänge zwischen den Bundesstaaten besser zu verstehen.

Da die reale Welt äußerst kompliziert sein kann (in Bezug auf die Art und Weise, wie Datenwerte variieren oder miteinander interagieren), sind Modelle nützlich, weil sie Probleme vereinfachen, so dass wir sie besser verstehen können (und dann effektivere Entscheidungen treffen können). Einerseits müssen die Modelle also so einfach sein, dass wir sie problemlos für unsere Entscheidungen nutzen können, andererseits müssen sie aber auch flexibel genug sein, um komplexe Situationen gut abbilden zu können. Glücklicherweise sind im Laufe der Jahre viele statistische Modelle entwickelt worden, die einen wirksamen Ausgleich zwischen diesen beiden Kriterien bieten. Ein solches Modell, das einen guten Ausgangspunkt für die komplizierteren Modelle bietet, die wir später betrachten, ist die Normalverteilung.

Aus statistischer Sicht ist eine Wahrscheinlichkeitsverteilung ein theoretisches Modell, das beschreibt, wie eine Zufallsvariable variiert. Für unsere Zwecke stellt eine Zufallsvariable die Datenwerte dar, die in der Bevölkerung von Interesse sind, z. B. die Verkaufspreise aller Einfamilienhäuser in unserem Wohnungsmarkt. Eine Möglichkeit, die Verteilung der Datenwerte in der Bevölkerung darzustellen, ist ein Histogramm, wie in Abschnitt 1.1 beschrieben. Der Unterschied besteht nun darin, dass das Histogramm die gesamte Grundgesamtheit und nicht nur die Stichprobe anzeigt. Da die Grundgesamtheit so viel größer ist als die Stichprobe, können die Bins des Histogramms (die aufeinanderfolgenden Bereiche der Daten, die die horizontalen Intervalle für die Balken bilden) viel kleiner sein. Die folgende Abbildung zeigt beispielsweise ein Histogramm für eine simulierte Grundgesamtheit von 1.000 Verkaufspreisen.

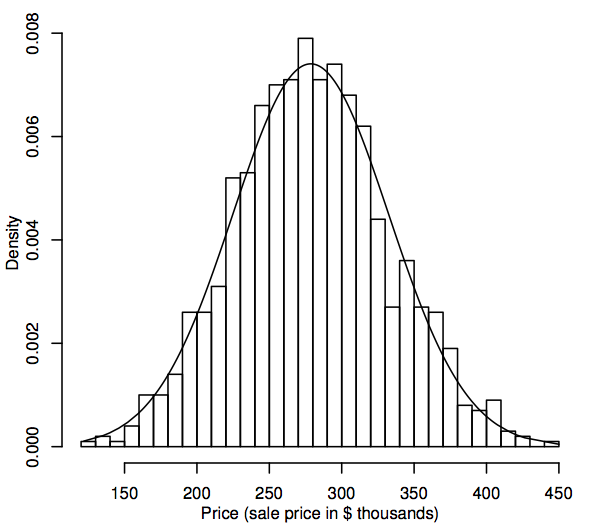
Wenn die Grundgesamtheit größer wird, können wir uns vorstellen, dass die Balken des Histogramms dünner und zahlreicher werden, bis das Histogramm eher einer glatten Kurve als einer Reihe von Stufen ähnelt. Diese glatte Kurve wird als Dichtekurve bezeichnet und kann als theoretische Version des Bevölkerungshistogramms betrachtet werden. Dichtekurven bieten auch eine Möglichkeit zur Visualisierung von Wahrscheinlichkeitsverteilungen wie der Normalverteilung. Eine normale Dichtekurve wird dem obigen Histogramm überlagert. Das simulierte Bevölkerungshistogramm folgt der Kurve recht genau, was darauf hindeutet, dass diese simulierte Bevölkerungsverteilung der Normalverteilung recht nahe kommt.

Um zu sehen, wie eine theoretische Verteilung sich als nützlich erweisen kann, um statistische Schlüsse über Populationen wie die in unserem Hauspreisbeispiel zu ziehen, müssen wir die Normalverteilung genauer betrachten. Zunächst betrachten wir eine bestimmte Version der Normalverteilung, die Standardnormalverteilung, die durch die folgende Dichtekurve dargestellt wird.

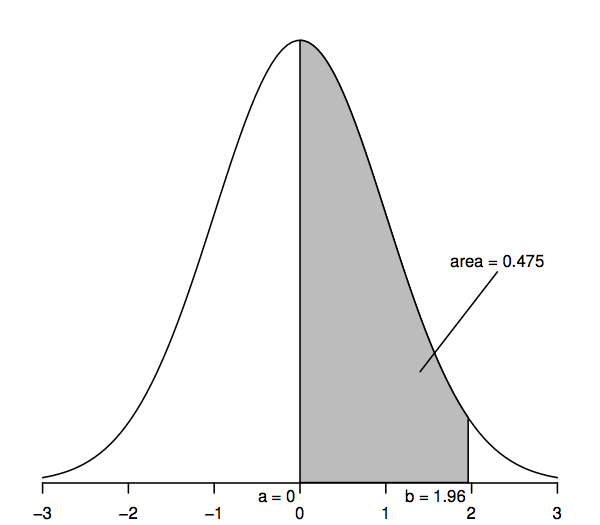
Zufallsvariablen, die einer Standardnormalverteilung folgen, haben einen Mittelwert von 0 (die Kurve ist also symmetrisch um 0, was unter dem höchsten Punkt der Kurve liegt) und eine Standardabweichung von 1 (die Kurve hat also einen Wendepunkt – wo die Kurve erst in die eine und dann in die andere Richtung abknickt – bei +1 und -1). Die normale Dichtekurve wird manchmal als „Glockenkurve“ bezeichnet, da ihre Form der einer Glocke ähnelt.

Das Hauptmerkmal der normalen Dichtekurve, das uns statistische Rückschlüsse ermöglicht, ist, dass die Flächen unter der Kurve Wahrscheinlichkeiten darstellen. Die gesamte Fläche unter der Kurve ist eins, während die Fläche unter der Kurve zwischen einem Punkt auf der horizontalen Achse (z.B. a) und einem anderen Punkt (z.B. b) die Wahrscheinlichkeit darstellt, dass eine Zufallsvariable, die einer Standardnormalverteilung folgt, zwischen a und b liegt.475, dass eine standardnormale Zufallsvariable zwischen a=0 und b=1,96 liegt, da die Fläche unter der Kurve zwischen a=0 und b=1,96 0,475 beträgt.

Wir können Werte für diese Flächen oder Wahrscheinlichkeiten aus einer Vielzahl von Quellen erhalten: Zahlentabellen, Taschenrechner, Tabellenkalkulations- oder Statistiksoftware, Websites usw. Im Folgenden werden nur einige ausgewählte Werte abgedruckt, da die meisten der späteren Berechnungen eine Verallgemeinerung der Normalverteilung, die so genannte „t-Verteilung“, verwenden. Außerdem ist es sinnvoller, statt der schraffierten Bereiche in der obigen Abbildung die „Schwanzbereiche“ zu betrachten (z. B, Um die Konsistenz mit den späteren Zahlentabellen zu gewährleisten, ermöglicht die folgende Tabelle die Berechnung solcher Schwanzbereiche:

Insbesondere beträgt der obere Schwanzbereich rechts von 1,96 0,025; dies ist gleichbedeutend mit der Aussage, dass der Bereich zwischen 0 und 1,96 0,475 beträgt (da die gesamte Fläche unter der Kurve 1 ist und die Fläche rechts von 0 0 0,5 ist). In ähnlicher Weise ist die Fläche mit zwei Ausläufern, die sich aus der Summe der Flächen rechts von 1,96 und links von -1,96 ergibt, zweimal 0,025 oder 0,05.

Wie hilft uns all dies, statistische Schlüsse über Populationen wie die in unserem Beispiel der Hauspreise zu ziehen? Der Grundgedanke ist, dass wir ein Normalverteilungsmodell an unsere Stichprobendaten anpassen und dann dieses Modell verwenden, um Rückschlüsse auf die entsprechende Population zu ziehen. So können wir beispielsweise Wahrscheinlichkeitsberechnungen für eine Normalverteilung (wie in der Abbildung oben dargestellt) verwenden, um Wahrscheinlichkeitsaussagen über eine Population zu treffen, die mit dieser Normalverteilung modelliert wurde – wie das genau geht, zeigen wir in Abschnitt 1.3. Bevor wir dies tun, halten wir jedoch inne, um einen Aspekt dieser Schlussfolgerungssequenz zu betrachten, der über Erfolg oder Misserfolg des Prozesses entscheiden kann. Bietet das Modell eine ausreichend gute Annäherung an das Muster der Stichprobenwerte, so dass wir sicher sein können, dass das Modell die Werte der Grundgesamtheit angemessen wiedergibt? Je besser die Annäherung, desto zuverlässiger sind unsere Schlussfolgerungen.

Wir haben vorhin gesehen, dass eine Dichtekurve als ein Histogramm mit einem sehr großen Stichprobenumfang betrachtet werden kann. Eine Möglichkeit zu beurteilen, ob unsere Population einem Normalverteilungsmodell folgt, besteht also darin, ein Histogramm aus unseren Stichprobendaten zu erstellen und visuell festzustellen, ob es „normal aussieht“, d. h. annähernd symmetrisch und glockenförmig ist. Dies ist eine etwas subjektive Entscheidung, aber mit etwas Erfahrung sollten Sie feststellen, dass es einfacher wird, eindeutig nicht-normale Histogramme von solchen zu unterscheiden, die einigermaßen normal sind. Während das obige Histogramm beispielsweise eindeutig wie eine normale Dichtekurve aussieht, ist die Normalität des Histogramms von 30 Musterverkaufspreisen in Abschnitt 1.1 weniger sicher. Eine vernünftige Schlussfolgerung in diesem Fall wäre, dass dieses Stichprobenhistogramm zwar nicht perfekt symmetrisch und glockenförmig ist, aber nahe genug, dass das entsprechende (hypothetische) Populationshistogramm durchaus normal sein könnte.

Eine alternative Möglichkeit zur Bewertung der Normalität besteht darin, ein QQ-Diagramm (Quantil-Quantil-Diagramm) zu erstellen, das auch als Normalwahrscheinlichkeitsdiagramm bekannt ist, wie hier für die Hauspreisdaten gezeigt:

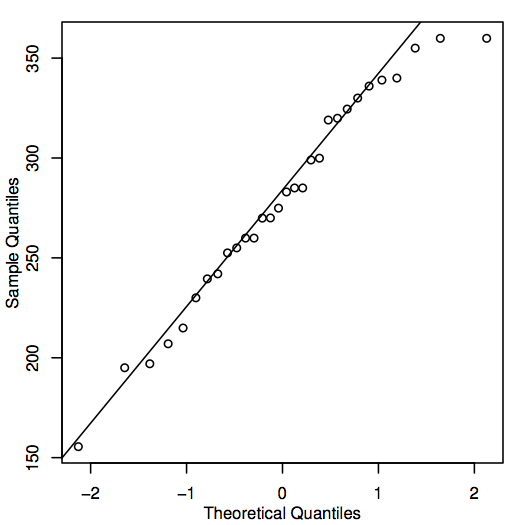
Wenn die Punkte im QQ-Diagramm nahe an der Diagonalen liegen, dann könnten die entsprechenden Bevölkerungswerte durchaus normal sein. Liegen die Punkte im Allgemeinen weit von der Linie entfernt, so ist die Normalität in Frage gestellt. Auch hier handelt es sich um eine eher subjektive Entscheidung, die mit zunehmender Erfahrung leichter zu treffen ist. In diesem Fall liegen die Punkte in Anbetracht des relativ kleinen Stichprobenumfangs wahrscheinlich nahe genug an der Linie, so dass man davon ausgehen kann, dass die Werte der Grundgesamtheit normal sein könnten.

Es gibt auch eine Reihe von quantitativen Methoden zur Beurteilung der Normalität – siehe Abschnitt 6.3.