Eine illustrierte Erklärung der Durchführung von 2D-Faltungen mit Matrixmultiplikationen

In diesem Artikel werde ich erklären, wie 2D-Faltungen als Matrixmultiplikationen implementiert werden. Diese Erklärung basiert auf den Notizen der CS231n Convolutional Neural Networks for Visual Recognition (Modul 2). Ich gehe davon aus, dass der Leser mit dem Konzept einer Faltungsoperation im Zusammenhang mit einem tiefen neuronalen Netz vertraut ist. Falls nicht, finden Sie in diesem Repo einen Bericht und ausgezeichnete Animationen, die erklären, was Faltungen sind. Der Code zur Reproduktion der Berechnungen in diesem Artikel kann hier heruntergeladen werden.

Kleines Beispiel

Angenommen, wir haben ein einkanaliges 4 x 4 Bild, X, und seine Pixelwerte sind wie folgt:

Angenommen, wir definieren eine 2D-Faltung mit den folgenden Eigenschaften:

Eigenschaften der 2D-Faltungsoperation, die wir an unserem Bild durchführen wollen

Das bedeutet, dass es 9 2 x 2 Bildfelder gibt, die elementweise mit der Matrix W multipliziert werden, wie folgt:

Alle möglichen 2 x 2 Bildfelder in X unter Berücksichtigung der Parameter der 2D-Faltung. Jede Farbe steht für ein eindeutiges Feld

Diese Bildfelder können als 4-dimensionale Spaltenvektoren dargestellt und zu einer einzigen 4 x 9-Matrix, P, verkettet werden, wie folgt:

Beachte, dass die i-te Spalte der Matrix P tatsächlich das i-te Bildfeld in Form eines Spaltenvektors ist.

Die Matrix der Gewichte für die Faltungsschicht, W, kann zu einem 4-dimensionalen Zeilenvektor , K, wie folgt abgeflacht werden:

W als abgeflachter Zeilenvektor K

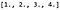
Um die Faltung durchzuführen, multiplizieren wir zunächst die Matrix K mit P, um einen 9-dimensionalen Zeilenvektor (1 x 9 Matrix) zu erhalten, was uns ergibt:

Das Ergebnis von K P

Dann formen wir das Ergebnis von K P in die richtige Form um, die eine 3 x 3 x 1-Matrix ist (letzte Kanaldimension). Die Kanaldimension ist 1, weil wir die Ausgangsfilter auf 1 gesetzt haben. Die Höhe und Breite ist 3, weil laut den CS231n-Notizen:

Formel zur Berechnung der Höhe nach Anwendung einer Faltungsoperation auf ein Bild. Die Formel zur Berechnung der Breite ist dieselbe (ersetzen Sie einfach die Bildhöhe und die Kernelhöhe durch die Bildbreite bzw. die Kernelbreite

Das bedeutet, dass das Ergebnis der Faltung gleich ist:

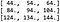
Endresultat der Faltung mit Matrixmultiplikationen

Was sich herausstellt, wenn wir die Faltung mit den in PyTorch eingebauten Funktionen durchführen (siehe den Begleitcode dieses Artikels für Details).

Größeres Beispiel

Das Beispiel im vorherigen Abschnitt geht von einem einzigen Bild aus und die Ausgangskanäle der Faltung sind 1. Was würde sich ändern, wenn wir diese Annahmen lockern?

Lassen Sie uns annehmen, dass unsere Eingabe für die Faltung ein 4 x 4 Bild mit 3 Kanälen mit den folgenden Pixelwerten ist:

Pixelwerte in unserem 4 x 4 x 3-Eingabebild

Was unsere Faltung betrifft, so werden wir sie so einstellen, dass sie die gleichen Eigenschaften wie im vorherigen Abschnitt hat, außer dass ihre Ausgangsfilter 2 sind. Das bedeutet, dass die anfängliche Gewichtungsmatrix W die Form (2, 2, 2, 3) haben muss, d.h. (Ausgangsfilter, Kernelhöhe, Kernelbreite, Kanäle des Eingangsbildes). Wir setzen W auf die folgenden Werte:

Werte für W bei einem 2 x 2 Kernel, 2 Ausgangsfilter und 3-Kanal-Eingangsbild

Beachten Sie, dass jeder Ausgangsfilter seinen eigenen Kernel hat (deshalb haben wir in diesem Beispiel 2 Kernel) und dass jeder Kernel 3 Kanäle hat (da das Eingangsbild 3 Kanäle hat).

Da wir immer noch einen 2 x 2-Kernel auf ein 4 x 4-Bild mit 0 Zero-Padding und Stride 1 falten, ist die Anzahl der Bildfelder immer noch 9. Die Matrix der Bildfelder, P, wird jedoch anders sein. Genauer gesagt ist die i-te Spalte von P die Verkettung der Werte des 1., 2. und 3. Kanals (als Spaltenvektor), die dem Bildfeld i entsprechen. P ist nun eine 12 x 9 Matrix. Die Zeilen sind 12, weil jedes Bildfeld 3 Kanäle hat und jeder Kanal 4 Elemente hat, da wir die Kernelgröße auf 2 x 2 festgelegt haben. So sieht P aus:

Wie bei W wird jeder Kernel in einen Zeilenvektor abgeflacht und zeilenweise verkettet, um eine 2 x 12-Matrix, K, zu bilden. Die i-te Zeile von K ist die Verkettung der Werte des ersten, zweiten und dritten Kanals (in Form eines Zeilenvektors), die dem i-ten Kernel entsprechen. So sieht K aus:

Die 2 x 12-Matrix der abgeflachten Kernelwerte in W, K

Nun muss nur noch die Matrixmultiplikation K P durchgeführt und in die richtige Form gebracht werden. Die korrekte Form ist eine 3 x 3 x 2-Matrix (letzte Kanaldimension). Hier ist das Ergebnis der Multiplikation:

Das Ergebnis von K P, eine 2 x 9 Matrix

Und hier ist das Ergebnis nach der Umformung in eine 3 x 3 x 2 Matrix:

Endgültiges Ergebnis der Faltung mit Hilfe von Matrixmultiplikationen

Was wiederum überprüft wird, wenn wir die Faltung mit den in PyTorch eingebauten Funktionen durchführen (siehe den Begleitcode dieses Artikels für Details).

So What?

Warum sollten wir uns darum kümmern, 2D-Faltungen in Form von Matrixmultiplikationen auszudrücken? Neben einer effizienten Implementierung, die für die Ausführung auf einem Grafikprozessor geeignet ist, ermöglicht uns die Kenntnis dieses Ansatzes, Aussagen über das Verhalten eines tiefen neuronalen Faltungsnetzwerks zu treffen. Zum Beispiel haben He et. al. (2015) 2D-Faltungen in Form von Matrixmultiplikationen ausgedrückt, was es ihnen ermöglichte, die Eigenschaften zufälliger Matrizen/Vektoren anzuwenden, um eine bessere Gewichte-Initialisierungsroutine zu finden.

Abschluss

In diesem Artikel habe ich anhand von zwei kleinen Beispielen erklärt, wie man 2D-Faltungen mit Matrixmultiplikationen durchführt. Ich hoffe, dass dies für Sie ausreichend ist, um auf beliebige Eingangsbilddimensionen und Faltungseigenschaften zu verallgemeinern. Lassen Sie mich in den Kommentaren wissen, wenn etwas unklar ist.

1D-Faltung

Die in diesem Artikel beschriebene Methode lässt sich auch auf 1D-Faltungen verallgemeinern.

Angenommen, die Eingabe ist ein 12-dimensionaler 3-Kanal-Vektor wie folgt:

Eine Eingabe, die ein 12-D-Vektor mit 3 Kanälen ist

Wenn wir unsere 1D-Faltung mit den folgenden Parametern einstellen:

Kernelgröße: 1 x 4
Ausgangskanäle: 2
Stride: 2
Padding: 0
Bias: 0

Dann sind die Parameter der Faltungsoperation, W, ein Tensor der Form (2 , 3, 1, 4). Setzen wir W auf die folgenden Werte:

Werte für W. Man beachte, dass jeder Kernel ein (3, 1, 4)-Tensor ist

Ausgehend von den Parametern der Faltungsoperation hat die Matrix der „Bild“-Felder P die Form (12, 5) (5 Bildfelder, wobei jedes Bildfeld ein 12-D-Vektor ist, da ein Feld 4 Elemente über 3 Kanäle hat) und sieht wie folgt aus:

Als Nächstes flachen wir W ab, um K zu erhalten, das die Form (2, 12) hat, da es 2 Kernel gibt und jeder Kernel 12 Elemente hat. So sieht K aus:

Werte von K, einer 2 x 12 Matrix

Nun können wir K mit P multiplizieren, was ergibt:

Das Ergebnis von K P, eine 2 x 5 Matrix

Schließlich formen wir K P in die richtige Form um, die nach der Formel ein „Bild“ mit der Form (1, 5) ist. Das heißt, das Ergebnis dieser Faltung ist ein Tensor mit der Form (2, 1, 5), da wir die Ausgangskanäle auf 2 gesetzt haben. So sieht das Endergebnis aus:

Das Ergebnis von K P nach der Umformung in die korrekte Form

Was erwartungsgemäß funktioniert, wenn wir die Faltung mit den in PyTorch eingebauten Funktionen durchführen würden.