Bayesian Belief Network oder Bayesian Network oder Belief Network ist ein Probabilistisches Graphisches Modell (PGM), das bedingte Abhängigkeiten zwischen Zufallsvariablen durch einen Directed Acyclic Graph (DAG) darstellt.
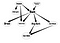
Heute werde ich versuchen, die Hauptaspekte von Belief-Netzen zu erläutern, insbesondere für Anwendungen, die mit der Analyse sozialer Netzwerke (SNA) in Verbindung stehen können. Außerdem zeige ich Ihnen eine Beispielimplementierung dieser Art von Netzwerk.
Wofür verwenden wir Bayes’sche Netzwerke?
Bayes’sche Netzwerke werden in vielen Bereichen eingesetzt. Zum Beispiel Krankheitsdiagnose, optimierte Websuche, Spam-Filterung, genregulatorische Netze, usw. Und diese Liste kann noch erweitert werden. Das Hauptziel dieser Netze besteht darin, die Struktur der Kausalitätsbeziehungen zu verstehen. Um dies zu verdeutlichen, betrachten wir ein Problem der Krankheitsdiagnose. Bei gegebenen Symptomen und der daraus resultierenden Krankheit konstruieren wir unser Belief Network, und wenn ein neuer Patient kommt, können wir daraus ableiten, welche Krankheit oder Krankheiten der neue Patient haben könnte, indem wir Wahrscheinlichkeiten für jede Krankheit angeben. In ähnlicher Weise können diese Kausalitätsbeziehungen auch für andere Probleme konstruiert werden, und die Inferenztechniken können zu interessanten Ergebnissen führen.
Kurzer Überblick über die Wahrscheinlichkeit
Bevor wir fortfahren, möchte ich Ihnen zur Auffrischung unseres Gedächtnisses die Definition der bedingten Eigenschaft geben. Die bedingte Wahrscheinlichkeit ist die Wahrscheinlichkeit einer Zufallsvariablen, wenn eine andere Zufallsvariable gegeben ist. Sie wird gezeigt durch
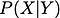
Wenn diese beiden Zufallsvariablen abhängig sind,
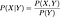
Wenn sie unabhängig sind, dann
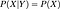
Mathematische Definition von Vertrauensnetzen
Die Wahrscheinlichkeiten werden berechnet in den Glaubensnetzen durch die folgende Formel
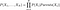
Wie man aus der Formel entnehmen kann, müssen wir, um die gemeinsame Verteilung berechnen zu können, über die vom Netz angegebenen bedingten Wahrscheinlichkeiten verfügen. Aber wenn wir die gemeinsame Verteilung haben, können wir anfangen, interessante Fragen zu stellen. Im ersten Beispiel fragen wir nach der Wahrscheinlichkeit von „REGEN“, wenn „JAHRESZEIT“ „WINTER“ ist und „HUND BELLT“ „WAHR“ ist.
Python-Beispiel für Belief Network
So, ich denke, das reicht an Theorie und wir sehen uns ein echtes Beispiel mit meiner derzeitigen Lieblingsprogrammiersprache Python an ❤️ Bevor wir fortfahren, kannst du das Jupyter Notebook, das ich geschrieben habe, hier finden.
# create the nodes
season = BbnNode(Variable(0, 'season', ), )
atmos_pres = BbnNode(Variable(1, 'atmos_press', ), )
allergies = BbnNode(Variable(2, 'allergies', ), )
rain = BbnNode(Variable(3, 'rain', ), )
grass = BbnNode(Variable(4, 'grass', ), )
umbrellas = BbnNode(Variable(5, 'umbrellas', ), )
dog_bark = BbnNode(Variable(6, 'dog_bark', ), )
cat_mood = BbnNode(Variable(7, 'cat_mood', ), )
cat_hide = BbnNode(Variable(8, 'cat_hide', ), )bbn = Bbn() \
.add_node(season) \
.add_node(atmos_pres) \
.add_node(allergies) \
.add_node(rain) \
.add_node(grass) \
.add_node(umbrellas) \
.add_node(dog_bark) \
.add_node(cat_mood) \
.add_node(cat_hide) \
.add_edge(Edge(season, allergies, EdgeType.DIRECTED)) \
.add_edge(Edge(season, umbrellas, EdgeType.DIRECTED)) \
.add_edge(Edge(season, rain, EdgeType.DIRECTED)) \
.add_edge(Edge(atmos_pres, rain, EdgeType.DIRECTED)) \
.add_edge(Edge(rain, grass, EdgeType.DIRECTED)) \
.add_edge(Edge(rain, umbrellas, EdgeType.DIRECTED)) \
.add_edge(Edge(rain, dog_bark, EdgeType.DIRECTED)) \
.add_edge(Edge(rain, cat_mood, EdgeType.DIRECTED)) \
.add_edge(Edge(dog_bark, cat_hide, EdgeType.DIRECTED)) \
.add_edge(Edge(cat_mood, cat_hide, EdgeType.DIRECTED))
Wir haben zuerst unsere Knoten mit bedingten Wahrscheinlichkeiten beschrieben. Sie sollten bemerken, dass ich der Einfachheit halber einige mögliche Zustandswerte übersprungen habe. Zum Beispiel kann die Variable „Jahreszeit“ auch die Werte „Frühling“ und „Herbst“ annehmen. Die Idee ist also die gleiche.
Nicht, lassen Sie uns überprüfen, ob unser Netzwerk richtig konstruiert ist oder nicht.
with warnings.catch_warnings():
warnings.simplefilter('ignore')
graph = convert_for_drawing(bbn)
pos = nx.nx_agraph.graphviz_layout(graph, prog='neato')plt.figure(figsize=(20, 10))
plt.subplot(121)
labels = dict()
nx.draw(graph, pos=pos, with_labels=True, labels=labels)
plt.title('BBN DAG')
Dieser Codeschnipsel würde den folgenden Graphen ergeben
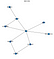
Sie sehen also, dass dieses Netzwerk mit meiner ausgefallenen Zeichnung am Anfang übereinstimmt. Lassen Sie uns nun einige Schlüsse aus diesem Belief Network ziehen.
# convert the BBN to a join tree
join_tree = InferenceController.apply(bbn)# insert an observation evidence
ev = EvidenceBuilder() \
.with_node(join_tree.get_bbn_node_by_name('season')) \
.with_evidence('winter', 1.0) \
.build()join_tree.set_observation(ev)# print the marginal probabilities
for node in join_tree.get_bbn_nodes():
potential = join_tree.get_bbn_potential(node)
print(node)
print(potential)
print('--------------------->')
Dieser Codeschnipsel gibt dem Netzwerk im Grunde die Evidenz, dass die Jahreszeit Winter mit einer Wahrscheinlichkeit von 1,0 ist. Nach diesem Beweis, wenn wir die Inferenz tun, erhalten wir folgende Ergebnisse.
0|season|winter,summer
0=winter|1.00000
0=summer|0.00000
--------------------->
2|allergies|allergic,non_alergic
2=allergic|0.70000
2=non_alergic|0.30000
--------------------->
3|rain|rainy,sunny
3=rainy|0.80000
3=sunny|0.20000
--------------------->
4|grass|grass,no_grass
4=grass|0.70000
4=no_grass|0.30000
--------------------->
1|atmos_press|high,low
1=high|0.50000
1=low|0.50000
--------------------->
5|umbrellas|on,off
5=on|0.95200
5=off|0.04800
--------------------->
6|dog_bark|bark,not_bark
6=bark|0.66000
6=not_bark|0.34000
--------------------->
7|cat_mood|good,bad
7=good|0.23000
7=bad|0.77000
--------------------->
8|cat_hide|hide,show
8=hide|0.87150
8=show|0.12850
--------------------->
Wenn wir weitere Beweise hinzufügen, wie der Hund nicht bellt
# convert the BBN to a join tree
join_tree = InferenceController.apply(bbn)# insert an observation evidence
ev = EvidenceBuilder() \
.with_node(join_tree.get_bbn_node_by_name('season')) \
.with_evidence('winter', 1.0) \
.build()ev2 = EvidenceBuilder() \
.with_node(join_tree.get_bbn_node_by_name('dog_bark')) \
.with_evidence('not_bark', 1.0) \
.build()join_tree.set_observation(ev)
join_tree.set_observation(ev2)# print the marginal probabilities
for node in join_tree.get_bbn_nodes():
potential = join_tree.get_bbn_potential(node)
print(node)
print(potential)
print('--------------------->')
Wir erhalten die folgenden Inferenzergebnisse
0|season|winter,summer
0=winter|1.00000
0=summer|0.00000
--------------------->
2|allergies|allergic,non_alergic
2=allergic|0.70000
2=non_alergic|0.30000
--------------------->
3|rain|rainy,sunny
3=rainy|0.47059
3=sunny|0.52941
--------------------->
4|grass|grass,no_grass
4=grass|0.53529
4=no_grass|0.46471
--------------------->
1|atmos_press|high,low
1=high|0.39706
1=low|0.60294
--------------------->
5|umbrellas|on,off
5=on|0.88941
5=off|0.11059
--------------------->
6|dog_bark|bark,not_bark
6=bark|0.00000
6=not_bark|1.00000
--------------------->
7|cat_mood|good,bad
7=good|0.52647
7=bad|0.47353
--------------------->
8|cat_hide|hide,show
8=hide|0.83162
8=show|0.16838
--------------------->
Siehst du den Unterschied? 😆 Viele Wahrscheinlichkeitswerte geändert, wenn wir den Beweis im Zusammenhang mit dem Bellen hinzufügen. Es ist definitiv ein dummes Beispiel, aber schön, um eine Intuition zu bekommen.
Wie verwendet man Bayes’sche Netze in SNA?
Bayes’sche Netze sind sehr mächtige Werkzeuge, um die Struktur der Kausalitätsbeziehungen zwischen Variablen zu verstehen. Sobald Sie Ihr Modell entworfen haben, kann es Ihnen selbst bei einem kleinen Datensatz verschiedene Dinge sagen. Die Frage in diesem Teil ist, wie man die Vorteile von Bayes’schen Netzen in SNA nutzen kann. Die Antwort ist nicht eindeutig, aber lassen Sie uns mit einer tiefgreifenden Idee beginnen. In SNA versuchen wir, die Struktur eines sozialen Netzwerks zu verstehen. Darüber hinaus versuchen wir, die Bedeutung der Knoten zu verstehen. Aber wir wissen nicht, was die Ergebnisse unserer Wichtigkeitsmetriken sind. Dies ist der Punkt, an dem Bayes’sche Netzwerke ansetzen. Wenn man zum Beispiel annimmt, dass die Wichtigkeit eines Knotens durch die Grad-Zentralität und die Link-Zentralität bestimmt wird, könnte man das folgende Netzwerk haben.
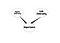
Dies ist ein sehr naives Bayes’sches Netzwerk. Zusätzlich zur Bestimmung der Wichtigkeit der Knoten kann eine weitere Anwendung die Suche nach einem bestimmten Knotentyp sein. Betrachten wir ein soziales Netzwerk, in dem es einige Personen gibt, die potenzielle Führungspersönlichkeiten sind, und ich möchte nach ihnen suchen. Betrachten wir den folgenden Graphen
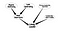
Dieses etwas kompliziertere Netzwerk wird uns helfen, die Unsicherheit der Knoten zu bestimmen, die mit einer Führungsrolle in Verbindung stehen.
Eine weitere Anwendung wäre das Ableiten der Links. Die neuen Verbindungen können aus den bestehenden abgeleitet werden. Zum Beispiel kann von der Gruppenzugehörigkeit in einem sozialen Netzwerk auf die wahrscheinliche Mitgliedschaft geschlossen werden. Was ich meinte, ist, dass wir eine neue Verbindung zwischen Benutzern und Gruppen modellieren können, indem wir bestehende Verbindungen berücksichtigen. Siehe das folgende Modelldiagramm
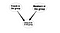
So, das sind einige grundlegende Beispiele dafür, wie Bayes’sche Netzwerke in SNA angewendet werden können. Dieses Thema ist nicht sehr gut erforscht, aber ich denke, es könnte sehr nützlich sein, um es weiter zu erforschen.
Schlussfolgerung
Das Schwierige an Bayes’schen Netzen ist das Design. Vor allem, wenn man an SNA denkt, ist das Konstruieren eines Mappings von sozialen Netzwerken mit einem Bayes’schen Netzwerk eher eine Kunst als eine Wissenschaft 😃 Aber wenn man die Kunst einmal gemacht hat und sein Modell sehr gut entworfen hat, können diese praktischen Werkzeuge einem eine Menge Dinge sagen. Wie wir wissen, werden Bayes’sche Netzwerke in vielen Bereichen eingesetzt. In den meisten Fällen haben sie sehr gut funktioniert. Daher bin ich der festen Überzeugung, dass wir auch bei sozialen Netzwerken sehr tiefgreifende Schlüsse ziehen können.
Für weitere Untersuchungen mit SNA und Bayes’schen Netzwerken bleiben Sie bitte dran 🚀