Die Klassifizierung ist ein überwachter Ansatz des maschinellen Lernens, bei dem der Algorithmus aus den ihm zur Verfügung gestellten Daten lernt – und dieses Lernen dann dazu verwendet, neue Beobachtungen zu klassifizieren.
Mit anderen Worten, der Trainingsdatensatz wird verwendet, um bessere Randbedingungen zu erhalten, die zur Bestimmung der einzelnen Zielklassen verwendet werden können; sobald diese Randbedingungen bestimmt sind, besteht die nächste Aufgabe darin, die Zielklasse vorherzusagen.
Binäre Klassifikatoren arbeiten mit nur zwei Klassen oder möglichen Ergebnissen (Beispiel: positive oder negative Stimmung; ob der Kreditgeber den Kredit auszahlen wird oder nicht; usw.), und Multiklassenklassifikatoren arbeiten mit mehreren Klassen (Beispiel: zu welchem Land eine Flagge gehört, ob ein Bild ein Apfel oder eine Banane oder eine Orange ist; usw.). Bei Multiklassen-Klassifikatoren wird davon ausgegangen, dass jede Probe nur einem einzigen Label zugeordnet ist.

Einer der ersten populären Algorithmen für die Klassifizierung im Bereich des maschinellen Lernens war Naive Bayes, ein probabilistischer Klassifikator, der durch das Bayes-Theorem inspiriert wurde (das es uns ermöglicht, begründete Rückschlüsse auf Ereignisse in der realen Welt auf der Grundlage des Vorwissens über Beobachtungen zu ziehen, die darauf hindeuten könnten). Der Name („Naive“) rührt daher, dass der Algorithmus von der Annahme ausgeht, dass die Attribute bedingt unabhängig sind.
Der Algorithmus ist einfach zu implementieren und stellt in der Regel eine vernünftige Methode dar, um mit der Klassifizierung zu beginnen. Er kann leicht auf größere Datensätze skaliert werden (er benötigt lineare Zeit im Gegensatz zur iterativen Annäherung, wie sie für viele andere Arten von Klassifikatoren verwendet wird, die in Bezug auf die Rechenressourcen teurer ist) und erfordert eine geringe Menge an Trainingsdaten.
Naive Bayes kann jedoch unter einem Problem leiden, das als „Nullwahrscheinlichkeitsproblem“ bekannt ist, wenn die bedingte Wahrscheinlichkeit für ein bestimmtes Attribut gleich Null ist und keine gültige Vorhersage liefert. Eine Lösung ist der Einsatz eines Glättungsverfahrens (z. B. Laplace-Methode).

P(c|x) ist die Posteriorwahrscheinlichkeit der Klasse (c, Ziel) bei gegebenem Prädiktor (x, Attribute). P(c) ist die vorherige Wahrscheinlichkeit der Klasse. P(x|c) ist die Likelihood, d.h. die Wahrscheinlichkeit des Prädiktors bei gegebener Klasse, und P(x) ist die Priorwahrscheinlichkeit des Prädiktors.
Im ersten Schritt des Algorithmus geht es darum, die Priorwahrscheinlichkeit für gegebene Klassenetiketten zu berechnen. Dann wird die Wahrscheinlichkeit mit jedem Attribut für jede Klasse ermittelt. Anschließend werden diese Werte in die Bayes-Formel & eingesetzt, um die posteriore Wahrscheinlichkeit zu berechnen und dann zu sehen, welche Klasse eine höhere Wahrscheinlichkeit hat, wenn die Eingabe zu der Klasse mit der höheren Wahrscheinlichkeit gehört.
Es ist ziemlich einfach, Naive Bayes in Python zu implementieren, indem man die scikit-learn-Bibliothek nutzt. Es gibt drei Arten von Naive Bayes-Modellen in der scikit-learn-Bibliothek: (a) Gauß-Typ (geht davon aus, dass die Merkmale einer glockenartigen Normalverteilung folgen), (b) Multinomial (wird für diskrete Zählungen verwendet, d. h. für die Anzahl der Male, die ein Ergebnis über x Versuche hinweg beobachtet wird) und (c) Bernoulli (nützlich für binäre Merkmalsvektoren; ein beliebter Anwendungsfall ist die Textklassifizierung).
Ein anderer beliebter Mechanismus ist der Entscheidungsbaum. Aus einer Reihe von Attributen und deren Klassen erzeugt der Baum eine Folge von Regeln, die zur Klassifizierung der Daten verwendet werden können. Der Algorithmus teilt die Stichprobe in zwei oder mehr homogene Gruppen (Blätter) auf der Grundlage der signifikantesten Unterscheidungsmerkmale in den Eingangsvariablen. Um ein Unterscheidungsmerkmal (Prädiktor) auszuwählen, berücksichtigt der Algorithmus alle Merkmale und führt eine binäre Aufteilung durch (bei kategorischen Daten: Aufteilung nach Katze; bei kontinuierlichen Daten: Auswahl eines Grenzwerts). Er wählt dann das Merkmal mit den geringsten Kosten (d. h. der höchsten Genauigkeit) und wiederholt dies rekursiv, bis er die Daten erfolgreich in alle Blätter aufteilt (oder die maximale Tiefe erreicht).
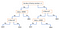
Entscheidungsbäume sind im Allgemeinen einfach zu verstehen und zu visualisieren und erfordern nur wenig Datenvorbereitung. Außerdem kann diese Methode sowohl numerische als auch kategoriale Daten verarbeiten. Andererseits lassen sich komplexe Bäume nicht gut verallgemeinern („overfitting“), und Entscheidungsbäume können etwas instabil sein, da kleine Variationen in den Daten dazu führen können, dass ein völlig anderer Baum generiert wird.
Eine von Entscheidungsbäumen abgeleitete Klassifizierungsmethode ist Random Forest, im Wesentlichen ein „Meta-Schätzer“, der eine Reihe von Entscheidungsbäumen auf verschiedene Unterstichproben von Datensätzen anpasst und den Durchschnitt verwendet, um die Vorhersagegenauigkeit des Modells zu verbessern und over-fitting zu kontrollieren. Die Größe der Unterstichprobe ist die gleiche wie die Größe der ursprünglichen Eingangsstichprobe – aber die Stichproben werden mit Ersetzung gezogen.
Random Forests neigen dazu, ein höheres Maß an Robustheit gegenüber Overfitting (>Robustheit gegenüber Rauschen in den Daten) zu zeigen, mit effizienter Ausführungszeit auch bei größeren Datensätzen. Sie sind jedoch empfindlicher für unausgewogene Datensätze, sind aber auch etwas komplexer zu interpretieren und erfordern mehr Rechenressourcen.
Ein weiterer beliebter Klassifikator in ML ist die logistische Regression – bei der die Wahrscheinlichkeiten, die die möglichen Ergebnisse eines einzelnen Versuchs beschreiben, mit einer logistischen Funktion modelliert werden (Klassifizierungsmethode trotz des Namens):

So sieht die logistische Gleichung aus:
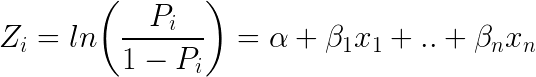
Wenn man e (Exponent) auf beiden Seiten der Gleichung einsetzt, ergibt sich:
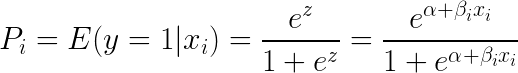
Die logistische Regression ist am nützlichsten, um den Einfluss mehrerer unabhängiger Variablen auf eine einzige Ergebnisvariable zu verstehen. Sie konzentriert sich auf die binäre Klassifizierung (für Probleme mit mehreren Klassen verwenden wir Erweiterungen der logistischen Regression wie die multinomiale und ordinale logistische Regression). Die logistische Regression ist in vielen Anwendungsfällen beliebt, z. B. bei der Kreditanalyse und der Reaktions-/Kaufbereitschaft.
Zu guter Letzt wird auch kNN (für „k Nearest Neighbors“) häufig für Klassifizierungsprobleme verwendet. kNN ist ein einfacher Algorithmus, der alle verfügbaren Fälle speichert und neue Fälle auf der Grundlage eines Ähnlichkeitsmaßes (z. B. Distanzfunktionen) klassifiziert. Es wurde bereits Anfang der 1970er Jahre als nichtparametrisches Verfahren in der statistischen Schätzung und Mustererkennung eingesetzt:

