Posted on

Phase (Wellen)

, Author

Die Phase einer Schwingung oder Welle ist der Bruchteil eines vollständigen Zyklus, der einer Verschiebung von einem bestimmten Bezugspunkt zum Zeitpunkt t = 0 entspricht. Die Phase ist ein Konzept aus dem Frequenzbereich oder dem Bereich der Fourier-Transformation und kann als solches leicht im Sinne einer einfachen harmonischen Bewegung verstanden werden. Dasselbe Konzept gilt für Wellenbewegungen, die entweder an einem Punkt im Raum über ein Zeitintervall oder über ein Raumintervall zu einem bestimmten Zeitpunkt betrachtet werden. Die einfache harmonische Bewegung ist eine Verschiebung, die zyklisch variiert, wie unten dargestellt:

Datei:Einfache harmonische Bewegung.png

und beschrieben durch die Formel:

{\displaystyle x(t)=A\cdot \sin(2\pi ft+\theta ),\,}

wobei A die Amplitude der Schwingung, f die Frequenz, t die verstrichene Zeit und {\displaystyle \theta } die Phase der Schwingung ist. Die Phase bestimmt oder wird bestimmt durch die Anfangsverschiebung zum Zeitpunkt t = 0. Eine Bewegung mit der Frequenz f hat die Periode {\displaystyle T={\frac {1}{f}}.}

Zwei mögliche Unklarheiten können festgestellt werden:

  • Eine ist, dass die Anfangsverschiebung von {\displaystyle \cos(2\pi ft+\theta )\,} anders ist als die Sinusfunktion, dennoch scheinen sie die gleiche „Phase“ zu haben.
  • Der zeitveränderliche Winkel {\displaystyle 2\pi ft+\theta ,\,} oder sein Modulo-Wert {\displaystyle 2\pi }, wird auch als „Phase“ bezeichnet. Sie ist dann keine Anfangsbedingung, sondern eine sich kontinuierlich verändernde Bedingung.

Der Begriff der momentanen Phase wird verwendet, um den zeitlich veränderlichen Winkel von der Anfangsbedingung zu unterscheiden. Er hat auch eine formale Definition, die auf allgemeinere Funktionen anwendbar ist und die Anfangsphase einer Funktion bei t=0 eindeutig definiert. D.h. Sinus und Kosinus haben von Natur aus unterschiedliche Anfangsphasen. Wenn nicht ausdrücklich etwas anderes angegeben ist, sollte im Allgemeinen auf den Kosinus geschlossen werden. (siehe auch Phasor)

Phasenverschiebung

Datei:Phasenverschiebung.png

Illustration der Phasenverschiebung. Die horizontale Achse stellt einen Winkel (Phase) dar, der mit der Zeit zunimmt.

{\displaystyle \theta } wird manchmal als Phasenverschiebung bezeichnet, weil sie eine „Verschiebung“ von der Nullphase darstellt. Aber eine Änderung von {\displaystyle \theta } wird auch als Phasenverschiebung bezeichnet.

Für unendlich lange Sinuskurven ist eine Änderung von {\displaystyle \theta } dasselbe wie eine zeitliche Verschiebung, wie eine Zeitverzögerung. Wenn {\displaystyle x(t)\,} um {\displaystyle {\begin{matrix}{\frac {1}{4}}\end{matrix}}\,} seines Zyklus verzögert (zeitlich verschoben) wird, wird es:

{\displaystyle x(t-{\begin{matrix}{\frac {1}{4}}\end{matrix}}T)\,} {\displaystyle =A\cdot \sin(2\pi f(t-{\begin{matrix}{\frac {1}{4}}\end{matrix}}T)+\theta )\,}
{\displaystyle =A\cdot \sin(2\pi ft-{\begin{matrix}{\frac {\pi }{2}}\end{matrix}}+\theta ),\,}

wessen „Phase“ nun {\displaystyle \theta -{\begin{matrix}{\frac {\pi }{2}}\end{matrix}} ist.} Es wurde um {\displaystyle {\begin{matrix}{\frac {\pi }{2}}\end{matrix}}} verschoben.

Phasendifferenz

Datei:Sinuswellen gleiche Phase.svg

Gleichphasige Wellen

File:Sine waves different phase.svg

Out-of-phase waves

File:Phase-shift illustration.png

Links: der Realteil einer ebenen Welle, die von oben nach unten läuft. Rechts: dieselbe Welle, nachdem ein mittlerer Teil eine Phasenverschiebung erfahren hat, z. B. beim Durchgang durch ein Glas mit anderer Dicke als die anderen Teile. (In der Abbildung rechts ist der Effekt der Beugung nicht berücksichtigt, der bei großen Entfernungen zunimmt).

Zwei Oszillatoren, die die gleiche Frequenz und unterschiedliche Phasen haben, weisen eine Phasendifferenz auf, und man sagt, dass die Oszillatoren zueinander phasenverschoben sind. Der Betrag, um den solche Oszillatoren aus dem Takt sind, kann in Grad von 0° bis 360° oder in Bogenmaß von 0 bis 2π ausgedrückt werden. Beträgt die Phasendifferenz 180 Grad (π Bogenmaß), so sind die beiden Oszillatoren gegenphasig. Treffen zwei interagierende Wellen an einem Punkt aufeinander, an dem sie gegenphasig sind, kommt es zur destruktiven Interferenz. Es kommt häufig vor, dass sich Wellen elektromagnetischer (Licht, HF), akustischer (Schall) oder anderer Energie in ihrem Übertragungsmedium überlagern. In diesem Fall bestimmt der Phasenunterschied, ob sie sich gegenseitig verstärken oder abschwächen. Bei Wellen mit gleichen Amplituden ist eine vollständige Auslöschung möglich.

Manchmal wird die Zeit (anstelle des Winkels) verwendet, um die Position innerhalb des Zyklus einer Schwingung auszudrücken.

  • Eine Phasendifferenz ist vergleichbar mit zwei Sportlern, die mit derselben Geschwindigkeit und in derselben Richtung um eine Rennstrecke laufen, aber an unterschiedlichen Positionen auf der Strecke starten. Sie passieren einen Punkt zu unterschiedlichen Zeitpunkten. Die Zeitdifferenz (Phasendifferenz) zwischen ihnen ist jedoch eine Konstante – sie ist bei jedem Durchlauf gleich, da sie mit derselben Geschwindigkeit und in dieselbe Richtung laufen. Hätten sie unterschiedliche Geschwindigkeiten (unterschiedliche Frequenzen), würde die Phasendifferenz nur unterschiedliche Ausgangspositionen widerspiegeln.
  • Wir messen die Erdrotation in Stunden, nicht in Bogenmaß. Und deshalb sind Zeitzonen ein Beispiel für Phasenunterschiede.

In-Phase und Quadratur (I&Q) Komponenten

Der Begriff In-Phase findet sich auch im Zusammenhang mit Kommunikationssignalen:

{\displaystyle A(t)\cdot \sin=I(t)\cdot \sin(2\pi ft)+Q(t)\cdot \underbrace {\cos(2\pi ft)} \sin \left(2\pi ft+{\begin{matrix}{\frac {\pi }{2}}\end{matrix}}\right)}}

und:

{\displaystyle A(t)\cdot \cos=I(t)\cdot \cos(2\pi ft)\underbrace {-Q(t)\cdot \sin(2\pi ft)} {+Q(t)\cdot \cos \left(2\pi ft+{\begin{matrix}{\frac {\pi }{2}}\end{matrix}}\right)}}

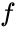
wobei {\displaystyle f\,} eine Trägerfrequenz darstellt, und

{\displaystyle I(t)\ {\stackrel {\mathrm {def} A(t)\cdot \cos,\,}{\displaystyle Q(t)\ {\stackrel {\mathrm {def} A(t)\cdot \sin.\,}

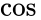
{\displaystyle A(t)\,} und {\displaystyle \phi (t)\,} stellen eine mögliche Modulation einer reinen Trägerwelle dar, z.B.: {\displaystyle \sin(2\pi ft).\,} Die Modulation verändert die ursprüngliche {\displaystyle \sin \,} Komponente des Trägers und erzeugt eine (neue) {\displaystyle \cos \,} Komponente, wie oben gezeigt. Die Komponente, die in Phase mit dem ursprünglichen Träger ist, wird als phasengleiche Komponente bezeichnet. Die andere Komponente, die immer um 90° ({\displaystyle {\begin{matrix}{\frac {\pi }{2}}\end{matrix}}} Radiant) „phasenverschoben“ ist, wird als Quadraturkomponente bezeichnet.

Phasenkohärenz

Kohärenz ist die Eigenschaft einer Welle, in verschiedenen Bereichen ihres Definitionsbereichs wohldefinierte Phasenbeziehungen aufzuweisen.

In der Physik schreibt die Quantenmechanik physikalischen Objekten Wellen zu. Die Wellenfunktion ist komplex, und da ihr quadratischer Modulus mit der Wahrscheinlichkeit der Beobachtung des Objekts verbunden ist, ist der komplexe Charakter der Wellenfunktion mit der Phase verbunden. Da die komplexe Algebra für den auffälligen Interferenzeffekt der Quantenmechanik verantwortlich ist, ist die Phase von Teilchen also letztlich mit ihrem Quantenverhalten verbunden.

Schreibe einen Kommentar

Deine E-Mail-Adresse wird nicht veröffentlicht.