(IUCr) Symbole für Symmetrieelemente

Acta Cryst. (1992). A48, 727-732

Abschlussbericht des Ad-Hoc-Komitees der International Union of Crystallography über die Nomenklatur der Symmetrie*

von P. M. DE WOLFF (Vorsitzender), Meermanstraat 126, 2614 AM Delft, Niederlande,

Y. BILLIET, Ecole Nationale d’Ingénieurs, BPW 3038 Sfax, Tunesien,

J. D. H. DONNAY, Department of Geological Sciences, McGill University, 3450 University Street, Montreal, Canada H3A 2A7,

W. FISCHER, Institut für Mineralogie, Petrologie und Kristallographie der Phillips-Universität, Lahnberge, D-3550 Marburg (Lahn), Deutschland,

R. B. GALIULIN, Institute of Crystallography, Academy of Sciences of Russia, Leninsky Prospekt 59, Moscow 117333, Russia,

A. M. GLAZER, Clarendon Laboratory, University of Oxford, Parks Road, Oxford OX1 3PU England,

TH. HAHN, Institut für Kristallographie, RWTH, Templergraben 55, D-5100 Aachen, Deutschland,

MARJORIE SENECHAL, Department of Mathematics, Smith College, Northampton, MA 01063, USA,

D. P. SHOEMAKER, Fachbereich Chemie, Oregon State University, OR 97331, USA,

H. WONDRATSCHEK, Institut für Kristallographie, Universität Karlsruhe, Kaiserstraße 12, D-7500 Karlsruhe 1, Deutschland,

A. J. C. WILSON (ex officio, IUCr Commission on International Tables), Crystallographic Data Centre, University Chemistry Laboratory, Lensfield Road, Cambridge CB2 1EW, England

und S. C. ABRAHAMS (ex officio, IUCr Commission on Crystallographic Nomenclature), Department of Physics, Southern Oregon State College, 1250 Siskiyou Boulevard, Ashland, OR 97520-5047, USA

(Erhalten am 7. November 1991; angenommen am 9. März 1992)

* Ernannt am 14. November 1984, geändert am 10. August 1987 gemäß den in Acta Cryst. (1979), A35, 1072. Der Abschlußbericht wurde am 23. Dezember 1991 von der IUCr-Kommission für kristallographische Nomenklatur und am 9. März 1992 vom Exekutivausschuß angenommen.

Abstract

Neue oder neu definierte Drucksymbole werden im Lichte der kürzlich akzeptierten Neudefinition der Symmetrieelemente vorgeschlagen. Insbesondere deckt der Buchstabe e bestimmte Gleitebenen ab, für die es bisher kein eindeutiges Symbol gab, wie z. B. diejenigen, die „entweder a oder b“ genannt werden. Die Verwendung von e im Hermann-Mauguin-Symbol von fünf verschiedenen Raumgruppen wird empfohlen. Für e-Ebenen, die in einer Richtung parallel zur Ebene projiziert werden, wird ein grafisches Symbol vorgeschlagen, das die Mehrdeutigkeit ihrer derzeitigen Bezeichnung beseitigt. Der Buchstabe k wird für eine neu definierte Klasse von Gleitebenen vorgeschlagen, für die es bisher kein spezifisches Symbol gab. Die Symbole für Symmetrieoperationen, die in den Raumgruppenbeschreibungen der International Tables for Crystallography (1989), Vol. A (Dordrecht: Kluwer Academic Publishers) eingeführt wurden, werden für den allgemeinen Gebrauch empfohlen, mit Änderungen nur für Gleitreflexionsoperationen.

Einführung

Der 1980 eingesetzte Ad-hoc-Ausschuss, der sich mit „Nomenklaturproblemen in Bezug auf Symmetrieoperationen und Symmetrieelemente in Raumgruppen“ befassen sollte, hat zwei Berichte herausgegeben: „Nomenklatur für Kristallfamilien, Bravais-Gittertypen und arithmetische Klassen“ (de Wolff et al., 1985) und Definition of Symmetry Elements in Space Groups and Point Groups (de Wolff et al., 1989). Wie im Bericht von 1989 erwähnt, besteht das einzige noch offene Problem bei den Symmetrieoperationen in der Wahl geeigneter Symbole, da das Konzept klar ist. Eine vorläufige Notation wurde in den International Tables for Crystallography (1983, 1989) angenommen, die im Folgenden als ITA83 bezeichnet wird.

Gedruckte Symbole für Symmetrieelemente

Die Definition der Symmetrieelemente, wie sie im Bericht von 1989 (de Wolff et al.) gegeben wurde, wird im gesamten vorliegenden Bericht verwendet. Hier wiederholen wir das Wesentliche:

Für jede gegebene Symmetrieoperation wird ihr geometrisches Element (Ebene, Punkt und/oder Linie) definiert. Ein Symmetrieelement ist die Kombination des geometrischen Elements einer der Symmetrieoperationen in einer gegebenen Raumgruppe mit der Menge (genannt „Elementmenge“) aller Symmetrieoperationen in dieser Raumgruppe, die dieses geometrische Element gemeinsam haben.

Explizite Definitionen der geometrischen Elemente und Beschreibungen der sich daraus ergebenden Symmetrieelemente sowie ihre Symbole sind in den Tabellen 1 und 2 enthalten (diese sind mit Ausnahme der Gleitebenen identisch mit den Tabellen 1 und 2 im Bericht von 1989 und werden hier der Vollständigkeit halber wiederholt, siehe unten). Jedes Symmetrieelement wird durch ein Symbol dargestellt, das aus zwei Zeichen besteht. Das erste Zeichen ist ein großgeschriebenes E für alle Symmetrieelemente. Es dient dazu, zu zeigen, dass sich das Symbol auf ein Symmetrieelement und nicht z. B. auf eine Symmetrieoperation bezieht. Ist dies bereits aus dem Kontext ersichtlich, so kann das E weggelassen werden, z. B. „eine Achse 2“ statt „eine Achse E2“.

Tabelle 1. Geometrische Elemente von Symmetrieoperationen in Punktgruppen und Raumgruppen
Symmetrieoperation	Geometrisches Element	Zusätzliche Parameter
Identität	Nicht erforderlich	Keine
Translation	Nicht erforderlich	Vektor $\mathbf{t}$
Reflexion in Ebene A	Ebene A	Keine
Gleitende Reflexion = Reflexion in Ebene A und Translation $\mathbf{v}$ parallel zu A	Ebene A	Gleitvektor $\mathbf{v}$
Rotation um Linie b	Linie b	Winkel und Drehsinn
Schraubendrehung = Drehung um Linie b und Translation $\mathbf{u}$ parallel zu b	Linie b	Winkel und Drehrichtung Schraubenvektor $\mathbf{u}$
Rotoinversion = Drehung um Linie b und Inversion durch Punkt P auf b	Linie b und Punkt P auf b	Winkel (ungleich $\pi$ ) und Drehsinn
Inversion durch Punkt P	Punkt P	Keine

Das im Bericht von 1989 aufgeführte Symbol Eg kann für Gleitebenen verwendet werden, wenn man lediglich zeigen will, dass das Symmetrieelement eine Gleitebene ist. Gehört es dagegen zu einer der besonderen Arten, die seit langem mit einem entsprechenden Buchstaben bezeichnet werden (a, b, c, n oder d; vgl. ITA83), dann ersetzt dieser Buchstabe g in Eg.

Tabelle 2. Symmetrieelemente in Punktgruppen und Raumgruppen
Name des Symmetrieelements	Symbol	Geometrisches Element	Definierende Operation (d.o.)	Operationen in Elementmenge
Spiegelebene	Em	Ebene A	Spiegelung in A	D.o. und seine koplanaren Äquivalente*
Gleitebene	Eg $\ddag$	Ebene A	Gleitende Reflexion in A, 2v (nicht v) eine Gittertranslation	D.o. und ihre koplanaren Äquivalente*
Rotationsachse	En	Linie b	Rotation um b, Winkel $2\pi/n$ ,n = 2, 3, 4 oder 6	1., $\punkte$ ,(n – 1)te Potenzen von d.o. und ihre koaxialen Äquivalente $\dag$
Schraubenachse	Enj	Linie b	Schraubendrehung um b, Winkel $2\pi/n$ , u =j/n mal kürzeste Gitter Translation entlang b, rechte Schraube; n = 2, 3, 4 oder 6, $j=1,\Punkte,(n-1)$	1., $\Punkte$ ,(n – 1)te Potenzen von d.o. und ihre koaxialen Äquivalente $\dag$
Rototationsachse	$E\bar n$	Linie b und Punkt P auf b	Rotationsumkehr: Drehung um b, Winkel $2\pi/n$ , und Inversion durch P; n = 3, 4 oder 6	D.o. und seine Inversion
Mitte	$E\bar 1$	Punkt P	Inversion durch P	D.o. nur

* Das heißt, alle Gleitreflexionen mit der gleichen Reflexionsebene, wobei sich die Gleitvektoren von denen des d.o. (der für eine Reflexion als Null angenommen wird) durch einen Gittertranslationsvektor unterscheiden.
$\dag$ Das heißt, alle Drehungen und Schraubendrehungen mit der gleichen Achse b, dem gleichen Winkel und Drehsinn und dem gleichen Schraubenvektor $\mathbf{u}$ (Null für eine Drehung) bis zu einem Gittertranslationsvektor.
$\ddag$ In Eg wird g durch a, b, c, n, d, e oder k für bestimmte Arten von Gleitebenen ersetzt, vgl. §2.

Ein wichtiger neuer Aspekt von Symbolen wie Eb kann jedoch hervorgehoben werden. Nach ITA83 bedeutete die Bezeichnung einer Ebene mit b lediglich, dass eine Gleitspiegelung in der Ebene mit einer Gleitkomponente b/2 entlang der b-Achse eine Symmetrieoperation ist. Diese Definition trifft sicherlich auf die in Abb. 1 dargestellte Situation zu.

Abb. 1. (Nach W. Fischer.) Die Elementmenge einer Eb-Gleitebene, dargestellt als eine Menge von Punkten oberhalb (+) und unterhalb (-) der Ebene, die durch Gleitreflexionen in der Ebene entstehen, ausgehend z. B. vom +-Zeichen oben links. Das Netz N von Translationen parallel zur Ebene (+ $\cdots$ + Vektoren) wird durch ein Netz dargestellt, das in diesem Fall rechteckig ist. Beide Kantenpaare sind parallel zu den Kristallachsen. Es gibt eine Gleitspiegelung mit ihrem Gleitvektor (+ $\cdots$ -) entlang der b-Achse.

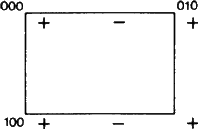
$\begin{figure} \includegraphics {fig1.ps} \end{figure}$

Abbildung 1 ist, ebenso wie die Abbildungen 2 und 3, einer Reihe ähnlicher Abbildungen entnommen, die von Ad-hoc-Ausschussmitglied W. Fischer als Inventar aller Typen von Gleitebenen entworfen wurden. Obwohl der Satz dem Ausschuss 1980 vorgelegt wurde, also lange vor der Veröffentlichung des Berichts von 1989, zeigt jede der Abbildungen genau den „Elementensatz“ des Gleitflugzeugs, wie er in diesem Bericht definiert wurde (vgl. die obige Zusammenfassung). Für eine Gleitebene besteht die Elementmenge aus allen Gleitreflexionen, die die Ebene als ihr gemeinsames geometrisches Element haben. Ihre Wirkung wird in Projektion auf diese Ebene dargestellt. Ausgehend von der Ausgangsposition eines beliebigen +-Vorzeichens ergibt sich jedes –Vorzeichen aus einer der Gleitreflexionen der Menge. Alle diese werden in einem elementaren Netz des sich ergebenden zweidimensionalen periodischen Musters von + und – Zeichen dargestellt.

Wir werden uns oft auf das Netz N beziehen, das durch alle Translationen parallel zur Ebene gebildet wird; dieses Netz lässt sich leicht veranschaulichen, wenn man nur die + Zeichen betrachtet. Diese Vektoren sind scharf zu unterscheiden von den Vektoren, die ein +-Zeichen mit einem beliebigen –Zeichen verbinden, von denen jeder der Gleitvektor einer zur Elementmenge gehörenden Gleitspiegelung ist.

Der neue Aspekt ergibt sich daraus, dass die b-Gleitebene in einigen Fällen nach der Definition von ITA83 auch eine a-Gleitebene ist; siehe Abb. 2. Dies ist natürlich nur dann der Fall, wenn das Netz N orthogonal zentriert ist, denn dann kann die a-Gleitebene durch Hinzufügen einer zentrierenden Translation in eine b-Gleitebene umgewandelt werden (und umgekehrt). Die bisherige Praxis bestand darin, eine solche Gleitebene willkürlich entweder a oder b zu nennen, was zu einer ungerechtfertigten Verzerrung und mangelnden Eindeutigkeit dieser Symbole führt. Wir schlagen daher vor, den Fall von Abb. 2 durch ein eigenes Symbol abzudecken.

Abb. 2. (Nach W. Fischer.) Die Elementmenge einer Ee-Gleitebene. Vgl. Beschriftung von Fig. 1. Man beachte, dass das Netz N hier orthogonal zentriert ist.

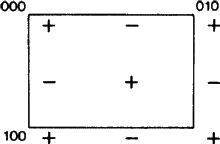
$\begin{figure} \includegraphics {fig2.ps} \end{figure}$

Der Anwendungsbereich dieses Symbols sollte dann auf Gleitebenen in diagonaler Ausrichtung, d. h. parallel zu nur einer Kristallachse, ausgedehnt werden, vorausgesetzt, dass die Gleitebene einen Gleitvektor entlang dieser Achse hat und dass das Netz N orthogonal zentriert ist. Für solche Ebenen gibt es nicht die Mehrdeutigkeit der obigen zufälligen Wahl a-b, sondern der erweiterte Geltungsbereich des neuen Symbols entspricht dem aller bestehenden Symbole (nämlich a, b, c, n und d). Jedes dieser Symbole wird für eine Gleitebene mit sowohl einer als auch zwei Kristallachsen im Netz N verwendet, vgl. Abb. 3.

Der Buchstabe e wird für das neue Symbol vorgeschlagen. Ee gilt also für Gleitebenen mit orthogonal zentrierten Netzen N und mindestens einem Gleitvektor entlang einer Kristallachse. Daher ist ein neues Kriterium erforderlich, nämlich die Orientierung der Gleitvektoren in Bezug auf die konventionellen Achsen des Kristalls. Da letztere entlang von Symmetrierichtungen verlaufen, während jede Gleitebene parallel zu einer Spiegelebene des Gitters verläuft, ist es nicht verwunderlich, dass es immer mindestens eine konventionelle Kristallachse in N gibt. Wenn es nur eine solche Achse gibt, dann gibt es senkrecht zu ihr immer eine weitere Translation in N.

Das neue Symbol e sowie die alten Symbole a, b, c, d, n werden nun in Bezug auf dieses neue Kriterium und den Bravais-Netztyp N neu definiert. Dieses Netz ist monoklin oder orthogonal oder tetragonal primitiv (mp oder op oder tp) oder orthogonal zentriert (oc). Nur Netze N vom Typ oc erlauben eine Ee-Gleitebene. Das Symbol En gilt für Netze N vom Bravais-Typ mp oder op, während Ed für Netze N vom oc-Typ gilt. (Wie in einer Fußnote zu Tabelle 1.3 in ITA83 angegeben: „Gleitebenen d kommen nur in orthorhombischen F-Raumgruppen, in tetragonalen I-Raumgruppen und in kubischen I- und F-Raumgruppen vor. Sie treten immer paarweise mit alternierenden Gleitvektoren auf“). Im Gegensatz zu den Ea-, Eb-, Ec- und Ee-Ebenen gibt es jedoch für die En- und Ed-Ebenen weder einen Gleitvektor parallel noch senkrecht zu einer konventionellen Achse in N.

Die folgenden Definitionen der Gleitebenen der oben genannten Arten sind in den Zeilen (i) und (ii) von Tabelle 3 und expliziter in Abb. 3 zusammengefasst.

Tabelle 3. Gedruckte Symbole für besondere Arten von Gleitebenen
Anzahl der Gleitvektoren parallel oder senkrecht zu den Kristallachsen im Netz N	Bravais-Typ des Netzes N
Das Symbol wird durch zwei Kriterien bestimmt. Das eine Kriterium ist der Bravais-Typ (mp, op, tp oder oc) des Netzes N, das durch die Symmetrieübersetzungen parallel zur betrachteten Ebene gebildet wird. Dieses Netz enthält immer mindestens eine konventionelle Kristallachse.* Das andere Kriterium bezieht sich auf die Orientierung der Gleitvektoren in Bezug auf diese Achsen.
	m, op, tp	oc
(i) Ein oder zwei parallele	Ec(Ea, Eb)	Ee
(ii) Keine parallele, keine senkrechte	En	Ed
(iii) Keine parallele, eine senkrechte	Ek	–

* Wie in ITA83, § 9.1; für rhomboedrische Raumgruppen werden hier jedoch nur hexagonale Achsen verwendet.

Alle übrigen Gleitebenen waren bisher ohne spezifisches Symbol. Sie haben jeweils eine diagonale Ausrichtung (nur eine konventionelle Kristallachse im Netz N). Unter den Gleitreflexionen in ihrer Elementmenge gibt es keine mit einem Gleitvektor entlang dieser Achse. Allerdings steht ein Gleitvektor (durch Symmetrie) senkrecht dazu. Das neue Symbol Ek wird in Zeile (iii) von Tabelle 3 kurz definiert und ist im unteren Block von Abb. 3 vollständig dargestellt. Einige Beispiele werden in § 2 gegeben.

Abb. 3. (Nach den Zeichnungen von W. Fisher.) Alle möglichen Aspekte der Elementensätze von Gleitebenen, dargestellt wie in Abb. 1, aber unabhängig von den Achsenbezeichnungen. Die Diagramme sind in Spalten gruppiert, die mit dem Bravais-Netz-Symbol (obere Zeile) des jeweiligen Netzes N überschrieben sind, vgl. Tabelle 3. Die anderen Kriterien dieser Tabelle werden überprüft, indem man zunächst die Doppellinien betrachtet, die die Richtungen der Kristallachsen in der Ebene anzeigen. Eine (vertikale) Kante des gezeigten Netzes von N wird immer entlang einer solchen Achse gewählt. Die andere Kante ist horizontal, außer in (1) und (8). Bei den Diagrammen (1), $\dots$ ,(5) ist das Gleitebenensymbol die Bezeichnung a, b oder c der vertikalen Achse; bei den anderen ist es der eingekreiste Buchstabe in dem umrandeten Block, der das Diagramm enthält. Man beachte die vertikalen Gleitvektoren in den Diagrammen (1), $\dots$ ,(7), die horizontalen in (6), (7), (14), (15) und das Fehlen beider in (8), $\dots$ ,(13). Ein Beispiel für das Vorkommen ist unter jedem Diagramm durch das Raumgruppensymbol und das Koordinatentripel der Ebene angegeben.

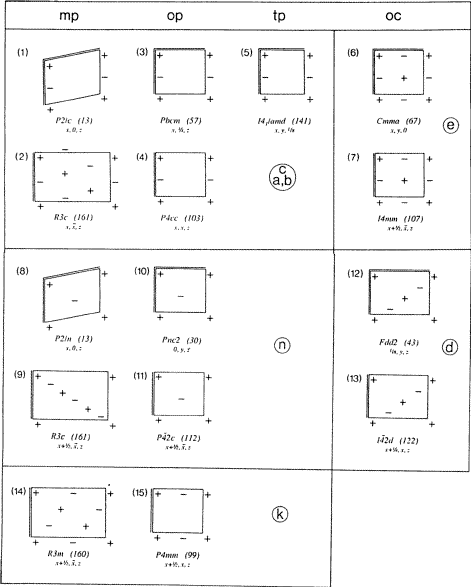
$\begin{figure} \includegraphics {fig3.ps} \end{figure}$

In Abb. 3 ist Fischers Inventar aller Typen von Gleitebenen in einer verkürzten – wenn auch immer noch vollständigen – Form dargestellt, in der den Kristallachsen mehr grafische Bedeutung beigemessen wurde. Für jedes Diagramm ist ein Beispiel für sein Vorkommen in einer Raumgruppe aufgeführt.

In einigen rhomboedrischen Raumgruppen treten diagonal orientierte Ec-, En- und Ek-Ebenen mit mp-Netzen N auf, die durch dreifache Zentrierung eines orthogonalen Netzes beschrieben werden können. Eine rechteckige Dreifachvermaschung des Netzes N ist für diese Arten von Gleitebenen in Abb. 3, Diagramme (2), (9) und (14) dargestellt. In Diagramm (9) erkennt man die Ähnlichkeit zu anderen n-Diagrammen wie (8) oder (10), wenn man in (9) ein monoklines Primitivnetz des Netzes N mit diagonalen Gleitvektoren betrachtet.

Grafische Symbole für Symmetrieelemente

Die bestehenden grafischen Symbole, wie sie in ITA83 definiert und verwendet wurden, werden vom Ad-hoc-Ausschuss mit einer Ausnahme als angemessen angesehen. Die Situation unterscheidet sich stark von derjenigen gedruckter Symbole, da in Zeichnungen die Projektionsrichtung ein zusätzlicher Parameter ist. In den im Folgenden verwendeten Begriffen „senkrechte Projektion“ und „parallele Projektion“ beziehen sich senkrecht und parallel auf die Orientierung der Projektionsrichtung in Bezug auf die Gleitebene.

Für eine Ee-Ebene existiert das Symbol 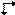für ihre senkrechte Projektion. Die vorhandenen grafischen Symbole für die Parallelprojektion einer Ee-Gleitebene leiden jedoch unter der gleichen Mehrdeutigkeit wie die gedruckten Symbole. Sie drücken den Gleitvektor entweder parallel oder senkrecht zur Projektionsrichtung aus, aber die Wahl ist willkürlich. Daher wird ein neues Symbol für die Parallelprojektion einer Ee-Gleitebene vorgeschlagen, nämlich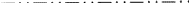

Beispiele für Ee-Ebenen.

Alle zu zwei Achsen parallelen Gleitebenen in den Raumgruppen Fmm2, Fmmm, $Fm\bar 3$ , $Fm\bar 3m$ und $Fm\bar 3c$ (Nr. 42, 69, 202, 225 und 226), sowie bestimmte Ebenen in den fünf in §3 aufgeführten Raumgruppen.

Diagonal orientierte Ee-Ebenen kommen in den Raumgruppen I4mm, I4cm, $I\bar 42m$ , I4/mmm, I4/mcm, $I\bar 43m$ und $Im\bar 3m$ (Nrn. 107, 108, 121, 139, 140, 217 und 229).

In ITA83 sind alle diese Ee-Ebenen eher willkürlich als gestrichelte oder gepunktete Linien in ihren Parallelprojektionen eingezeichnet. Abb. 4 zeigt das Diagramm der Raumgruppe I4cm (Nr. 108), sowohl wie in ITA83 dargestellt als auch unter Verwendung des neuen Symbols.

Abb. 4. (a) Diagramm der Raumgruppe I4cm (Nr. 108) aus ITA83. (b) Dasselbe, modifiziert durch Verwendung des in § 2 vorgeschlagenen graphischen Symbols für die Parallelprojektion einer Ee-Ebene.

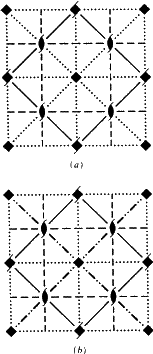
$\begin{figure} \includegraphics {fig4.ps} \end{figure}$

Obwohl Ek ein neues Drucksymbol ist, wurden in den Diagrammen von ITA83 alle Gleitebenen Ek zufriedenstellend mit denselben Konventionen gezeichnet, die für Ea/b/c-Gleitebenen verwendet werden. Wie in diesen Fällen gibt es einen einzigen speziellen Gleitvektor (senkrecht zur Kristallachse im Netz N, vgl. Tabelle 3). Wenn dieser Vektor z. B. parallel zur Projektionsebene verläuft, wird die Ek-Ebene immer als gestrichelte Linie gezeichnet, wie es die entsprechende Konvention vorschreibt. Daher wird kein neues graphisches Symbol für Ek-Gleitebenen vorgeschlagen.

Beispiele für Ek-Ebenen.

Solche Ebenen findet man in den Diagrammen von ITA83 leicht als Ebenen parallel zu nur einer Achse und als gestrichelte Linien projiziert, z.B. xxz in P4bm und $P\bar 42_1m$ (Nr. 100 und 113). Insbesondere die Tabelle 3 stimmt genau mit der Unterscheidung zwischen Ek- und En-Ebenen überein. Siehe z. B. die gestrichelten und punktgestrichelten Linien für R3m und R3c (Nr. 160 und 161).

Hermann-Mauguin-Raumgruppensymbole

Die Zeichen, die nach dem Gitterbuchstaben im Hermann-Mauguin (HM)-Symbol einer Raumgruppe erscheinen, sollten ursprünglich erzeugende Operationen der Gruppe darstellen. Zum Beispiel war b eine b-Gleitspiegelung in einer Ebene, die entsprechend ihrer Position im HM-Symbol orientiert war.

In der Praxis traten die beliebten, wenn auch schlecht definierten Symmetrieelemente an die Stelle der Operationen. So kam es, dass b als Gleitebene angesehen wurde, Eb in unserer heutigen Terminologie. Diese Umdeutung schadet nur dann nicht, wenn die Operation zu einer Ee-Gleitebene gehört. Wenn dies z. B. für die obige b-Gleitebene zutrifft, dann gibt es eine Ee-, aber keine Eb-Gleitebene in der entsprechenden Orientierung. In diesem Fall ist b ein sehr irreführendes Zeichen. Abgesehen davon ist die Bevorzugung von b gegenüber a oder c genauso störend wie bei den in §1 behandelten Symmetrieelement-Symbolen.

Es wird daher vorgeschlagen, solche irreführenden Buchstaben a oder b in allen fünf HM-Symbolen, in denen sie vorkommen, durch e zu ersetzen:

Raumgruppen-Nr.	39	41	64	67	68
Symbol in ITA83:	Abm2	Aba2	Cmca	Cmma	Ccca
Neues Symbol:	Aem2	Aea2	Cmce	Cmme	Ccce.

Ein weiterer Vorteil der vorgeschlagenen neuen Symbole ist, dass e – im Gegensatz zu a oder b – neutral ist und sich daher bei einer Achsenpermutation nicht ändert.

Gedruckte Symbole für Symmetrieoperationen

Ein vollständiger Satz von Drucksymbolen wurde von W. Fischer & E. Koch (ITA83, §11.2) entwickelt und in den Abschnitten über Symmetrieoperationen in den Raumgruppenbeschreibungen ausgiebig verwendet.

Kurz gesagt, besteht jedes Symbol aus bis zu drei Teilen. Der erste Teil ist ein einzelnes Zeichen (manchmal mit einem Index), das die Art der Operation beschreibt. Der oder die folgenden Teile geben die Komponenten eines relevanten Verschiebungs- oder Translationsvektors – immer in Klammern – und die Koordinaten des geometrischen Elements der Operation an, in dieser Reihenfolge.

Der Ad-hoc-Ausschuss möchte nach Prüfung dieses Systems zwei Änderungen für Gleitreflexionen einführen:

(i) anstelle des derzeitigen ersten Zeichens (das a, b, c, n, d oder g sein kann) immer den Buchstaben g schreiben;

(ii) die Gleitvektorkomponenten (in Klammern) immer vollständig schreiben, insbesondere für die einfachen Gleitreflexionen in a-, b- oder c-Gleitebenen, wo sie vorher weggelassen wurden.

Regel (i) unterdrückt Informationen über die Art der Gleitebene, zu der die Operation gehört. Sehr oft ist diese Information irrelevant oder sogar verwirrend. Für a/b/c-Ebenen kann die Unterdrückung wesentliche Informationen zerstören, aber der Verlust wird durch Regel (ii) wiederhergestellt, wie im folgenden Beispiel gezeigt.

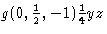Durch diese Änderungen wird die Einheitlichkeit der Symbole – auch in Bezug auf die Symbole für Drehungen – stark verbessert. Zum Beispiel stimmt das Symbol der Gleitreflexion in der Ebene $x = \frac{1}{4}$ , mit dem ungewöhnlichen Gleitvektor $(0, \frac{1}{2}, -1)$ , nämlich $g(0, \frac{1}{2}, 1) \frac{1}{4}yz$ , nun mit dem für eine einfache b-Gleitreflexion überein. In ITA83 wurde letztere mit $b \frac{1}{4} y z$ bezeichnet, aber dies wird durch Regel (ii) in $g(0, \frac{1}{2}, 0) \frac{1}{4} y z$ geändert.

Die obigen Regeln gelten auch für Gleitreflexionen, die zur Elementmenge einer Spiegelebene gehören. Wenn also die Verschiebungskomponente einer solchen Operation (0, 1, 2) ist, dann beginnt ihr Symbol mit g(0, 1, 2), nicht mit m(0, 1,2).

International Tables for Crystallography (1983). Vol. A, herausgegeben von TH. HAHN, insbesondere §§ 1.1, 1.3, 1.4, 7 und 11. Dordrecht: Kluwer Academic Publishers.

International Tables for Crystallography (1989). Vol. A, 2nd, revised, ed., edited by TH. HAHN. Dordrecht: Kluwer Academic Publishers.

WOLFF, P. M. DE, BELOV, N. V., BERTAUT, E. F., BUERGER, M. J., DONNAY, J. D. H., FISCHER, W., HAHN, TH., KOPTSIK, V. A., MACKAY, A. L., WONDRATSCHEK, H., WILSON, A. J. C. & ABRAHAMS, S. C. (1985). Acta Cryst. A41, 278-280.

WOLFF, P. M. DE, BILLIET, Y., DONNAY, J. D. H., FISCHER, W., GALIULIN, R. B., GLAZER, A. M., SENECHAL, M., SHOEMAKER, D. P., WONDRATSCHEK, H., HAHN, TH., WILSON, A. J. C. & ABRAHAMS, S. C. (1989). Acta Cryst. A45, 494-499.

…Vektoren. Die Gleitebenensymbole c, n und k für die drei Diagramme (2), (9) und (14) von Abb. 3 sind natürlich gemäß Tabelle 3 zugeordnet worden. Ein Mitglied des Ad-hoc-Ausschusses (Professor Wondratschek) ist der Meinung, dass das Symbol n für Diagramm (9) im Widerspruch zu den traditionellen Vorstellungen über n-Ebenen steht. Er schlägt vor, dem Diagramm (9) ein spezielles Symbol zuzuweisen. Dieser Vorschlag hat jedoch innerhalb des Ad-hoc-Ausschusses keine ausreichende Unterstützung gefunden.

Symbole für Symmetrieelemente und Symmetrieoperationen