Vaikka edellisen jakson menetelmät ovat käyttökelpoisia otosdatan kuvaamisessa ja esittämisessä, tilastotieteen todellinen teho paljastuu, kun käytämme otoksia saadaksemme tietoa populaatioista. Tässä yhteydessä populaatio on koko kiinnostavien kohteiden kokoelma, esimerkiksi kaikkien asuntomarkkinoiden omakotitalojen myyntihinnat, joita aineistomme edustaa. Haluaisimme tietää enemmän tästä populaatiosta auttaaksemme meitä tekemään päätöksen siitä, minkä kodin ostaisimme, mutta ainoa aineisto, joka meillä on käytössämme, on satunnainen otos 30:stä myyntihinnasta.
Voimme kuitenkin käyttää ”tilastollista ajattelua” tehdäksemme johtopäätöksiä kiinnostavasta populaatiosta analysoimalla otoksen tietoja. Käytämme erityisesti mallin käsitettä – matemaattista abstraktiota todellisesta maailmasta – jota sovitamme otosdataan. Jos tämä malli sopii kohtuullisesti aineistoon, eli jos se pystyy likimääräisesti kuvaamaan sitä tapaa, jolla aineisto vaihtelee, oletamme, että se pystyy likimääräisesti kuvaamaan myös perusjoukon käyttäytymistä. Malli tarjoaa tällöin perustan perusjoukkoa koskevien päätösten tekemiselle esimerkiksi tunnistamalla malleja, selittämällä vaihtelua ja ennustamalla tulevia arvoja. Tämä prosessi voi tietysti toimia vain, jos otoksen tietoja voidaan pitää populaatiota edustavina.
Joskus, vaikka tiedämme, että otosta ei ole valittu satunnaisesti, voimme silti mallintaa sitä. Tällöin emme ehkä pysty muodollisesti päättelemään populaatiosta otoksen perusteella, mutta voimme silti mallintaa otoksen taustalla olevaa rakennetta. Esimerkkinä voidaan mainita mukavuusotanta – otos, joka on valittu pikemminkin mukavuussyistä kuin sen tilastollisten ominaisuuksien perusteella. Kun mallinnetaan tällaisia otoksia, kaikki tulokset on raportoitava varoen rajoittamasta johtopäätöksiä otoksen kaltaisiin kohteisiin. Toinen esimerkki on, kun otos käsittää koko perusjoukon. Voisimme esimerkiksi mallintaa Yhdysvaltojen kaikkien 50 osavaltion tiedot, jotta ymmärtäisimme paremmin kaikkia osavaltioiden välisiä malleja tai systemaattisia yhteyksiä.
Koska reaalimaailma voi olla äärimmäisen monimutkainen (tavassa, jolla data-arvot vaihtelevat tai ovat vuorovaikutuksessa keskenään), mallit ovat hyödyllisiä, koska ne yksinkertaistavat ongelmia niin, että pystymme ymmärtämään niitä paremmin (ja tekemään sitten tehokkaampia päätöksiä). Yhtäältä tarvitsemme siis malleja, jotka ovat tarpeeksi yksinkertaisia, jotta voimme helposti käyttää niitä päätöksentekoon, mutta toisaalta tarvitsemme malleja, jotka ovat tarpeeksi joustavia antamaan hyviä approksimaatioita monimutkaisiin tilanteisiin. Onneksi vuosien varrella on kehitetty monia tilastollisia malleja, jotka tarjoavat tehokkaan tasapainon näiden kahden kriteerin välillä. Yksi tällainen malli, joka tarjoaa hyvän lähtökohdan myöhemmin tarkasteltaville monimutkaisemmille malleille, on normaalijakauma.
Todennäköisyysjakauma on tilastollisesta näkökulmasta teoreettinen malli, joka kuvaa satunnaismuuttujan vaihtelua. Meidän tarkoituksiamme varten satunnaismuuttuja edustaa perusjoukon kiinnostavia tietoarvoja, esimerkiksi kaikkien omakotitalojen myyntihintoja asuntomarkkinoillamme. Yksi tapa esittää tietoarvojen populaatiojakauma on histogrammi, kuten kohdassa 1.1 kuvattiin. Erona on nyt se, että histogrammi näyttää koko populaation eikä vain otosta. Koska populaatio on niin paljon suurempi kuin otos, histogrammin binit (peräkkäiset tietovälit, jotka muodostavat pylväiden vaakasuuntaiset välit) voivat olla paljon pienempiä, esimerkiksi seuraavassa on esitetty histogrammi simuloidulle 1000 myyntihinnan populaatiolle.
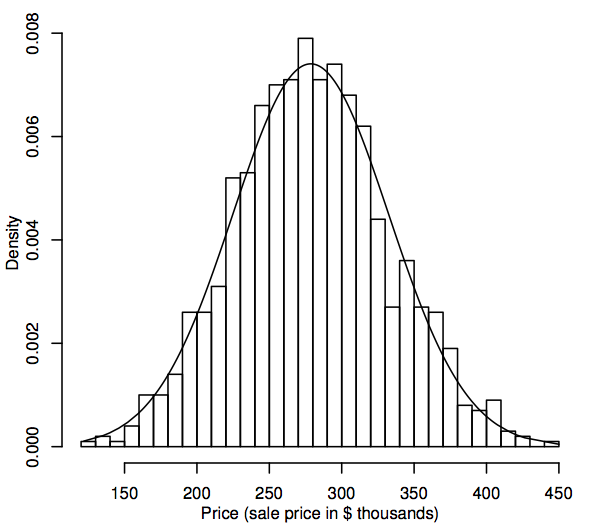
Kun populaation koko kasvaa, voimme kuvitella histogrammin pylväiden muuttuvan ohuemmiksi ja lukumäärältään suuremmiksi, kunnes histogrammi muistuttaa tasaista käyrästöä pikemminkin kuin sarjaa portaita. Tätä sileää käyrää kutsutaan tiheyskäyräksi, ja sitä voidaan ajatella teoreettisena versiona populaatiohistogrammista. Tiheyskäyrät tarjoavat myös tavan visualisoida todennäköisyysjakaumia, kuten normaalijakaumaa. Normaalin tiheyskäyrä on asetettu yllä olevan histogrammin päälle. Simuloitu väestöhistogrammi seuraa käyrää melko tarkasti, mikä viittaa siihen, että tämä simuloitu väestöjakauma on melko lähellä normaalijakaumaa.
Voidaksemme nähdä, miten teoreettinen jakauma voi osoittautua käyttökelpoiseksi tilastollisten päätelmien tekemisessä populaatioista, kuten esimerkissämme asuntojen hinnoista, meidän on tarkasteltava tarkemmin normaalijakaumaa. Aluksi tarkastelemme erästä tiettyä versiota normaalijakaumasta, standardinormaalijakaumaa, jota edustaa seuraava tiheyskäyrä.
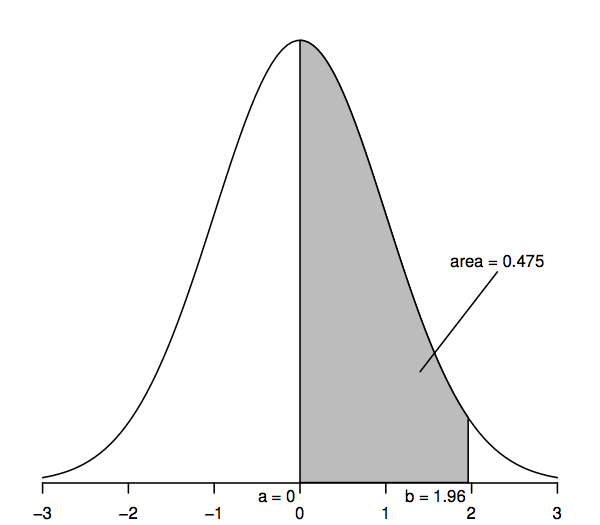
Standardinormaalijakaumaa noudattavilla satunnaismuuttujilla on keskiarvo 0 (joten käyrä on symmetrinen 0:n ympärillä, joka on käyrän ylimmän pisteen alapuolella) ja keskihajonta 1 (joten käyrällä on käännepiste – jossa käyrä taipuu ensin yhteen ja sitten toiseen suuntaan – pisteissä +1 ja -1). Normaalitiheyskäyrää kutsutaan joskus ”kellokäyräksi”, koska sen muoto muistuttaa kelloa.
Normaalitiheyskäyrän keskeinen piirre, jonka avulla voimme tehdä tilastollisia johtopäätöksiä, on se, että käyrän alapuoliset pinta-alat edustavat todennäköisyyksiä. Koko käyrän alle jäävä pinta-ala on yksi, kun taas vaaka-akselin yhden pisteen (vaikkapa a) ja toisen pisteen (vaikkapa b) välinen käyrän alle jäävä pinta-ala edustaa todennäköisyyttä, että satunnaismuuttuja, joka noudattaa vakionormaalijakaumaa, on a:n ja b:n välissä. Niinpä esimerkiksi yllä oleva kuva osoittaa, että todennäköisyys on 0.475 sille, että vakionormaalijakauman satunnaismuuttuja on välillä a=0 ja b=1,96, koska käyrän alle jäävä pinta-ala välillä a=0 ja b=1,96 on 0,475.
Voimme saada arvoja näille pinta-aloille tai todennäköisyyksille monista eri lähteistä: numerotaulukoista, laskimista, taulukkolaskentaohjelmista tai tilasto-ohjelmistoista, verkkosivuilta ja niin edelleen. Jäljempänä tulostamme vain muutamia valikoituja arvoja, koska useimmissa myöhemmissä laskelmissa käytetään normaalijakauman yleistystä, jota kutsutaan ”t-jakaumaksi”. Lisäksi yllä olevassa kuvassa tummennetun kaltaisten alueiden sijasta on hyödyllisempää tarkastella ”hännän alueita” (esim, pisteen b oikealla puolella), joten johdonmukaisuuden vuoksi myöhempien numerotaulukoiden kanssa seuraava taulukko mahdollistaa tällaisten häntäpinta-alojen laskemisen:
Etenkin ylemmän hännän pinta-ala 1,96:n oikealla puolella on 0,025; tämä vastaa sitä, että sanotaan, että 0:n ja 1,96:n välinen pinta-ala on 0,475 (koska koko pinta-ala käyrän alapuolella on 1 ja pinta-ala 0:n oikealla puolella on 0,5). Vastaavasti kahden hännän alue, joka on 1,96:n oikealla puolella ja -1,96:n vasemmalla puolella olevien alueiden summa, on kaksi kertaa 0,025 eli 0,05.
Miten tämä kaikki auttaa meitä tekemään tilastollisia johtopäätöksiä populaatioista, kuten esimerkissämme asuntojen hinnoista? Keskeinen ajatus on, että sovitamme normaalijakaumamallin otostietoihin ja käytämme sitten tätä mallia tehdessämme päätelmiä vastaavasta populaatiosta. Voimme esimerkiksi käyttää normaalijakauman todennäköisyyslaskelmia (kuten yllä olevassa kuvassa on esitetty) tehdäksemme todennäköisyysväittämiä populaatiosta, joka on mallinnettu käyttäen kyseistä normaalijakaumaa – näytämme tarkalleen, miten tämä tehdään luvussa 1.3. Ennen kuin teemme sen, pysähdymme kuitenkin pohtimaan erästä tähän päätelmäsekvenssiin liittyvää näkökohtaa, joka voi ratkaista prosessin. Antaako malli riittävän läheisen approksimaation otosarvojen mallille, jotta voimme olla varmoja siitä, että malli edustaa asianmukaisesti populaatioarvoja? Mitä parempi approksimaatio on, sitä luotettavampia ovat johtopäätöksemme.
Katsoimme aiemmin, miten tiheyskäyrää voidaan ajatella histogrammina, jossa on hyvin suuri otoskoko. Yksi tapa arvioida, noudattaako populaatiomme normaalijakaumamallia, on siis rakentaa histogrammi otosdatastamme ja määrittää visuaalisesti, näyttääkö se ”normaalilta”, eli suunnilleen symmetriseltä ja kellonmuotoiselta. Tämä on jokseenkin subjektiivinen päätös, mutta kokemuksen myötä sinun pitäisi huomata, että on helpompi erottaa selvästi epänormaalit histogrammit niistä, jotka ovat kohtuullisen normaaleja. Vaikka esimerkiksi edellä esitetty histogrammi näyttää selvästi normaalilta tiheyskäyrältä, kohdassa 1.1 esitetyn 30 näytteen myyntihintojen histogrammin normaalisuus ei ole yhtä varmaa. Järkevä johtopäätös tässä tapauksessa olisi, että vaikka tämä otoshistogrammi ei ole täysin symmetrinen ja kellonmuotoinen, se on riittävän lähellä sitä, että vastaava (hypoteettinen) populaatiohistogrammi voisi hyvinkin olla normaali.
Vaihtoehtoinen tapa arvioida normaaliutta on rakentaa QQ-plot (quantile-quantile plot), joka tunnetaan myös nimellä normaalitodennäköisyysplot, kuten tässä on esitetty asuntojen hintatietojen osalta:
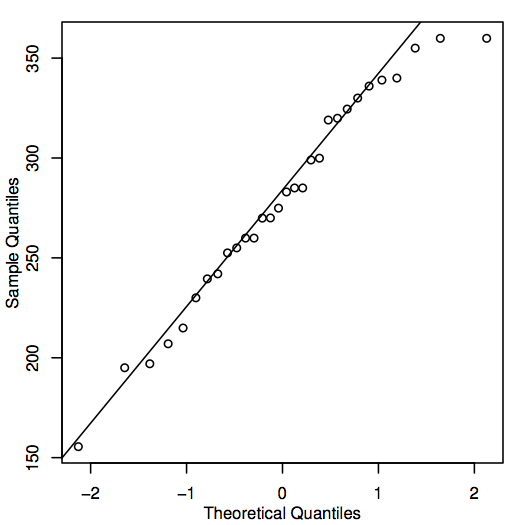
Jos QQ-plotin pisteet ovat lähellä diagonaaliviivaa, vastaavat populaatioarvot voisivat hyvinkin olla normaaleja. Jos pisteet sijaitsevat yleensä kaukana viivasta, normaalisuus on kyseenalainen. Tämäkin on jokseenkin subjektiivinen päätös, jonka tekeminen helpottuu kokemuksen myötä. Tässä tapauksessa, kun otetaan huomioon melko pieni otoskoko, pisteet ovat luultavasti tarpeeksi lähellä viivaa, joten on järkevää päätellä, että populaatioarvot voivat olla normaaleja.
Normaaliuden arvioimiseksi on myös olemassa erilaisia kvantitatiivisia menetelmiä – ks. kohta 6.3.