Määritelmä
Muuttujan x polynomi on funktio, joka voidaan kirjoittaa muodossa,
jossa an, an-1 , …, a2, a1, a0 ovat vakioita. Kutsumme termiä, joka sisältää x:n suurimman potenssin (eli anxn), johtavaksi termiksi ja an:tä johtavaksi kertoimeksi. Polynomin aste on x:n potenssi johtavassa termissä. Olemme jo nähneet asteen 0, 1 ja 2 polynomeja, jotka olivat vakio, lineaarinen ja kvadraattinen funktio. Astetta 3, 4 ja 5 olevilla polynomeilla on myös erikoisnimet: kuutiollinen, kvarttinen ja kvintinen funktio. Polynomeja, joiden aste n > 5, kutsutaan vain n-asteen polynomeiksi. Eri polynomifunktioiden nimet on tiivistetty alla olevaan taulukkoon.
| Polynomin aste | Funktion nimi |
| 0 | Konstanttifunktio |
| 1 | Lineaarinen funktio |
| 2 | kvadraattinen funktio |
| 3 | Kuutiofunktio |
| 4 | Neliöfunktio |
| 5 | Kuutiofunktio |
| n (jossa n > 5) | n:nnen asteen polynomi |
Esimerkkejä polynomeista mm:
Polynomien rajakäyttäytyminen
Funktion rajakäyttäytyminen kuvaa, mitä funktiolle tapahtuu, kun x → ±∞. Polynomin aste ja johtavan kertoimen merkki sanelevat sen rajakäyttäytymisen. Erityisesti
Nämä tulokset on tiivistetty alla olevaan taulukkoon.
Voit käyttää näitä tietoja määrittääksesi, onko polynomin aste pariton vai parillinen ja onko johtava kerroin positiivinen vai negatiivinen, yksinkertaisesti tarkastelemalla sen kuvaajaa.
Seuraavat polynomien kuvaajat ovat esimerkkejä jokaisesta yllä olevassa taulukossa esitetystä käyttäytymisestä.
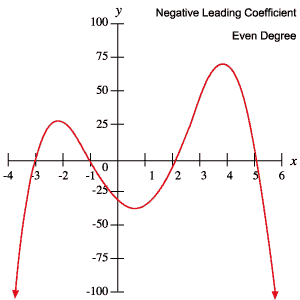
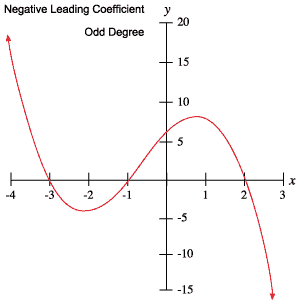
Juuret ja käännepisteet
Polynomin aste kertoo siitä vielä enemmän kuin rajakäyttäytyminen. Tarkemmin sanottuna n:nnen asteen polynomilla voi olla korkeintaan n reaalijuurta (x-keskipistettä tai nollakohtaa) kertalukuja laskien. Oletetaan esimerkiksi, että tarkastelemme 6. asteen polynomia, jolla on 4 erillistä juurta. Jos kahdella neljästä juuresta on kertaluku 2 ja kahdella muulla kertaluku 1, tiedämme, että muita juuria ei ole, koska olemme ottaneet huomioon kaikki kuusi juurta. Tämä johtuu siitä, että juuret, joiden kertaluku on kaksi (tunnetaan myös nimellä kaksoisjuuri), lasketaan kahdeksi juureksi.
Huomaa, että n:nnen asteen polynomilla ei tarvitse olla n reaalijuurta – sillä voi olla vähemmänkin, koska sillä on imaginäärijuuria. Huomaa, että parittoman asteen polynomilla on oltava vähintään yksi reaalijuuri, koska funktio lähestyy toisessa päässä – ∞ ja toisessa päässä + ∞; jatkuvan funktion, joka vaihtuu negatiivisesta positiiviseen, on leikattava x-akseli jossain välissä. Lisäksi n:nnen asteen polynomilla voi olla enintään n – 1 käännepistettä. Kääntöpiste on piste, jossa funktio muuttuu kasvavasta väheneväksi tai vähenevästä kasvavaksi, kuten alla olevassa kuvassa näkyy. Myös n:nnen asteen polynomilla ei tarvitse olla n-1 käännekohtaa, vaan niitä voi olla vähemmän.
Varoittava huomautus
On tärkeää ymmärtää ero parillisten ja parittomien funktioiden sekä parillisen ja parittoman asteen polynomien välillä. Mikä tahansa funktio f(x) on joko parillinen, jos,
f(-x) = x,
kaikkien f(x):n toimialueeseen kuuluvien x:ien osalta, tai pariton, jos,
f(-x) = -x,
kaikkien f(x):n toimialueeseen kuuluvien x:ien osalta,
kaikkien f(x):n toimialueeseen kuuluvien x:ien osalta,
tai sitten ei kumpikaan niistä ei ole parillinen eikä odd, jos kumpikaan edellä esitetyistä ei kelpaa.
K:n asteen polynomin, p(x), sanotaan olevan parillisen asteinen, jos k on parillinen luku ja parittoman asteinen, jos k on pariton luku. Muista, että vaikka p(x):llä olisi parillinen aste, se ei välttämättä ole parillinen funktio. Samoin jos p(x):llä on pariton aste, se ei välttämättä ole pariton funktio.
Käytämme termejä parillinen ja pariton myös kuvaamaan polynomien juuria. Tarkemmin sanottuna polynomilla p(x) on juurta x = a, jonka kertaluku on k (eli x = a on juuri, joka toistuu k kertaa), jos (x – a)k on p(x):n tekijä. Sanotaan, että x = a:lla on parillinen kertaluku, jos k on parillinen luku, ja pariton kertaluku, jos k on pariton luku.
Domain ja Range
Kaikilla polynomeilla on sama domain, joka koostuu kaikista reaaliluvuista. Parittoman asteen polynomien alue koostuu myös kaikista reaaliluvuista. Parillisen asteen polynomien alue on hieman monimutkaisempi, emmekä voi yksiselitteisesti ilmoittaa kaikkien parillisen asteen polynomien aluetta. Jos johtava kerroin on positiivinen, funktio ulottuu arvoon + ∞; jos taas johtava kerroin on negatiivinen, se ulottuu arvoon – ∞. Tämä tarkoittaa, että parillisen asteen polynomeilla, joiden etukerroin on positiivinen, on alue, jossa ymax tarkoittaa funktion saavuttamaa globaalia maksimia. Yleensä ei ole mahdollista määrittää analyyttisesti polynomien maksimeja tai minimejä.
*****
Seuraavassa osiossa opit polynomijakoa, tekniikkaa, jota käytetään polynomifunktioiden juurien etsimiseen.
Polynomijako