Bayesin uskomusverkko tai Bayesin verkko tai uskomusverkko on todennäköisyysgrafiikkamalli (Probabilistic Graphical Model, PGM), joka kuvaa satunnaismuuttujien välisiä ehdollisia riippuvuuksia suunnatun asyklisen graafin (Directed Acyclic Graph, DAG) avulla.
Tänään yritän selittää uskomusverkkojen keskeisiä näkökohtia erityisesti sovellusten osalta, jotka voivat liittyä sosiaaliseen verkostoanalyysiin(SNA). Lisäksi näytän esimerkkitoteutuksen tällaisesta verkosta.
Mihin käytämme Bayes-verkkoja?
Bayes-verkkoja sovelletaan monilla aloilla. Esimerkiksi sairauksien diagnosointi, optimoitu verkkohaku, roskapostin suodatus, geenien säätelyverkot jne. Ja tätä luetteloa voidaan laajentaa. Näiden verkkojen päätavoitteena on yrittää ymmärtää kausaalisuhteiden rakennetta. Tämän selventämiseksi tarkastellaan taudinmääritysongelmaa. Annettujen oireiden ja niistä johtuvan taudin avulla rakennamme uskomusverkostomme, ja kun uusi potilas tulee, voimme päätellä, mikä tauti tai mitkä taudit voivat olla uudella potilaalla antamalla todennäköisyydet kullekin taudille. Vastaavasti näitä kausaliteettisuhteita voidaan konstruoida muillekin ongelmille ja soveltaa päättelytekniikoita mielenkiintoisiin tuloksiin.
Pikakatselmus todennäköisyyksiin
Ennen kuin jatkamme, virkistääksemme muistiamme annan teille ehdollisen ominaisuuden määritelmän. Ehdollinen todennäköisyys on satunnaismuuttujan todennäköisyys, kun jokin toinen satunnaismuuttuja on annettu. Se osoitetaan
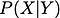
Jos nämä kaksi satunnaismuuttujaa ovat riippuvaisia,
Jos nämä ovat riippumattomia, niin
Matemaattinen määritelmä uskomusverkoille
Todennäköisyydet lasketaan uskomusverkoissa seuraavalla kaavalla
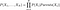
Kuten kaavan perusteella ymmärtäisit, että voidaksemme laskea yhteisjakauman tarvitsemme verkon osoittamat ehdolliset todennäköisyydet. Mutta edelleen, jos meillä on yhteinen jakauma, voimme alkaa esittää mielenkiintoisia kysymyksiä. Esimerkiksi ensimmäisessä esimerkissä kysymme ”SADEVEDEN” todennäköisyyttä, jos ”SYKSY” on ”TALVI” ja ”KOIRAN BARK” on ”TODELLINEN”.
Python-esimerkki uskomusverkosta
Niin, mielestäni tässä riittää teoria ja katsotaanpa todellinen esimerkki nykyisellä suosikkiohjelmointikielelläni Pythonilla ❤️ Ennen kuin jatkamme, löydät kirjoittamani Jupyter Notebookin täältä.
# create the nodes
season = BbnNode(Variable(0, 'season', ), )
atmos_pres = BbnNode(Variable(1, 'atmos_press', ), )
allergies = BbnNode(Variable(2, 'allergies', ), )
rain = BbnNode(Variable(3, 'rain', ), )
grass = BbnNode(Variable(4, 'grass', ), )
umbrellas = BbnNode(Variable(5, 'umbrellas', ), )
dog_bark = BbnNode(Variable(6, 'dog_bark', ), )
cat_mood = BbnNode(Variable(7, 'cat_mood', ), )
cat_hide = BbnNode(Variable(8, 'cat_hide', ), )bbn = Bbn() \
.add_node(season) \
.add_node(atmos_pres) \
.add_node(allergies) \
.add_node(rain) \
.add_node(grass) \
.add_node(umbrellas) \
.add_node(dog_bark) \
.add_node(cat_mood) \
.add_node(cat_hide) \
.add_edge(Edge(season, allergies, EdgeType.DIRECTED)) \
.add_edge(Edge(season, umbrellas, EdgeType.DIRECTED)) \
.add_edge(Edge(season, rain, EdgeType.DIRECTED)) \
.add_edge(Edge(atmos_pres, rain, EdgeType.DIRECTED)) \
.add_edge(Edge(rain, grass, EdgeType.DIRECTED)) \
.add_edge(Edge(rain, umbrellas, EdgeType.DIRECTED)) \
.add_edge(Edge(rain, dog_bark, EdgeType.DIRECTED)) \
.add_edge(Edge(rain, cat_mood, EdgeType.DIRECTED)) \
.add_edge(Edge(dog_bark, cat_hide, EdgeType.DIRECTED)) \
.add_edge(Edge(cat_mood, cat_hide, EdgeType.DIRECTED))
Kuvailimme ensin solmujamme ehdollisilla todennäköisyyksillä. Kannattaa huomata, että jätin yksinkertaisuuden vuoksi joitakin mahdollisia tila-arvoja väliin. Esimerkiksi vuodenaikamuuttuja ottaa muita arvoja ”kevät” ja ”syksy”. Idea on siis sama.
Ei, tarkistetaanpa, onko verkkomme rakennettu oikein vai ei.
with warnings.catch_warnings():
warnings.simplefilter('ignore')
graph = convert_for_drawing(bbn)
pos = nx.nx_agraph.graphviz_layout(graph, prog='neato')plt.figure(figsize=(20, 10))
plt.subplot(121)
labels = dict()
nx.draw(graph, pos=pos, with_labels=True, labels=labels)
plt.title('BBN DAG')
Tämän koodinpätkän tuloksena olisi seuraava kuvaaja
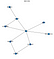
Näet siis, että tämä verkko sopii yhteen alussa tekemäni mielikuvituksellisen piirroksen kanssa. Tehdään nyt hieman päättelyä tälle uskomusverkolle.
# convert the BBN to a join tree
join_tree = InferenceController.apply(bbn)# insert an observation evidence
ev = EvidenceBuilder() \
.with_node(join_tree.get_bbn_node_by_name('season')) \
.with_evidence('winter', 1.0) \
.build()join_tree.set_observation(ev)# print the marginal probabilities
for node in join_tree.get_bbn_nodes():
potential = join_tree.get_bbn_potential(node)
print(node)
print(potential)
print('--------------------->')
Tämä koodinpätkä antaa periaatteessa todisteen verkolle, joka on vuodenaika on talvi 1.0 todennäköisyydellä. Tämän todisteen mukaan, kun teemme päättelyn, saamme seuraavat tulokset.
0|season|winter,summer
0=winter|1.00000
0=summer|0.00000
--------------------->
2|allergies|allergic,non_alergic
2=allergic|0.70000
2=non_alergic|0.30000
--------------------->
3|rain|rainy,sunny
3=rainy|0.80000
3=sunny|0.20000
--------------------->
4|grass|grass,no_grass
4=grass|0.70000
4=no_grass|0.30000
--------------------->
1|atmos_press|high,low
1=high|0.50000
1=low|0.50000
--------------------->
5|umbrellas|on,off
5=on|0.95200
5=off|0.04800
--------------------->
6|dog_bark|bark,not_bark
6=bark|0.66000
6=not_bark|0.34000
--------------------->
7|cat_mood|good,bad
7=good|0.23000
7=bad|0.77000
--------------------->
8|cat_hide|hide,show
8=hide|0.87150
8=show|0.12850
--------------------->
Kun lisäämme lisää todisteita, kuten että koira ei hauku
# convert the BBN to a join tree
join_tree = InferenceController.apply(bbn)# insert an observation evidence
ev = EvidenceBuilder() \
.with_node(join_tree.get_bbn_node_by_name('season')) \
.with_evidence('winter', 1.0) \
.build()ev2 = EvidenceBuilder() \
.with_node(join_tree.get_bbn_node_by_name('dog_bark')) \
.with_evidence('not_bark', 1.0) \
.build()join_tree.set_observation(ev)
join_tree.set_observation(ev2)# print the marginal probabilities
for node in join_tree.get_bbn_nodes():
potential = join_tree.get_bbn_potential(node)
print(node)
print(potential)
print('--------------------->')
Saatamme seuraavat päättelytulokset
0|season|winter,summer
0=winter|1.00000
0=summer|0.00000
--------------------->
2|allergies|allergic,non_alergic
2=allergic|0.70000
2=non_alergic|0.30000
--------------------->
3|rain|rainy,sunny
3=rainy|0.47059
3=sunny|0.52941
--------------------->
4|grass|grass,no_grass
4=grass|0.53529
4=no_grass|0.46471
--------------------->
1|atmos_press|high,low
1=high|0.39706
1=low|0.60294
--------------------->
5|umbrellas|on,off
5=on|0.88941
5=off|0.11059
--------------------->
6|dog_bark|bark,not_bark
6=bark|0.00000
6=not_bark|1.00000
--------------------->
7|cat_mood|good,bad
7=good|0.52647
7=bad|0.47353
--------------------->
8|cat_hide|hide,show
8=hide|0.83162
8=show|0.16838
--------------------->
Näetkö eron? 😆 Paljon todennäköisyyksien arvoja muuttui, kun lisäsimme todisteita, jotka liittyvät haukkumiseen. Se on varmasti typerä esimerkki, mutta mukava saada intuitio.
Miten Bayesin verkkoja käytetään SNA:ssa?
Bayesin verkot ovat erittäin tehokkaita työkaluja muuttujien välisten kausaalisuhteiden rakenteen ymmärtämiseen. Kun olet suunnitellut mallin, se voi pienelläkin aineistolla kertoa sinulle erilaisia asioita. Kysymys tässä osassa on, miten Bayes-verkoista voidaan saada hyötyä SNA:ssa. Vastaus ei ole yksiselitteinen, mutta lähdetään liikkeelle syvällisestä ajatuksesta. SNA:ssa yritämme ymmärtää sosiaalisen verkoston rakennetta. Lisäksi yritämme ymmärtää solmujen merkitystä. Mutta emme tiedä, että mitkä ovat tärkeysmittariemme tulokset. Tämä on se kohta, jossa Bayesin verkostot astuvat kuvaan. Jos esimerkiksi ajatellaan, että solmun tärkeys johtuu Degree Centralityn ja Link Centralityn perusteella, voidaan saada seuraava verkko.
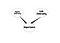
Tämä on hyvin naiivi Bayes-verkko. Solmujen tärkeyden määrittämisen lisäksi jatkosovelluksena voi olla jonkin tietyn tyyppisten solmujen etsiminen. Tarkastellaan sosiaalista verkostoa, jossa on joitakin ihmisiä, jotka ovat potentiaalisia johtajia, ja haluan etsiä heitä. Tarkastellaan seuraavaa graafia
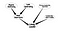
Tämä hieman monimutkaisempi verkko auttaa meitä määrittämään epävarmuuden solmuista, jotka liittyvät siihen, että ne voivat olla johtajia.
Muuten sovelluksena olisi linkkien päätteleminen. Uudet linkit voidaan päätellä olemassa olevista. Esimerkiksi sosiaalisen verkoston ryhmän jäsenyydestä voidaan päätellä todennäköinen jäsenyyslinkki. Tarkoitin, että voimme mallintaa uuden linkin käyttäjien ja ryhmien välille ottamalla huomioon olemassa olevat linkit. Katso seuraava mallikaavio
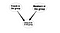
Näissä on siis joitain perustavanlaatuisia esimerkkejä siitä, miten Bayesin verkkoja voidaan soveltaa SNA:ssa. Tätä aihetta ei ole tutkittu kovin hyvin, mutta uskon, että sitä voisi olla erittäin hyödyllistä tutkia lisää.
Johtopäätös
Bayesin verkostojen vaikeinta on suunnittelu. Varsinkin, kun ajatellaan SNA:ta, kartoituksen rakentaminen sosiaalisesta verkostosta Bayesin verkoston avulla on enemmän taidetta kuin tiedettä 😃 Mutta kun olet tehnyt taidetyön ja suunnitellut mallisi hyvin, nämä kätevät työkalut voivat kertoa sinulle paljon asioita. Kuten tiedämme, Bayes-verkkoja käytetään monilla eri aloilla. Se toimi erittäin hyvin useimmissa tapauksissa. Siksi uskon vahvasti, että voimme tehdä hyvin syvällisiä johtopäätöksiä myös sosiaalisista verkostoista.
Jatkotutkimukset SNA:n ja Bayesin verkostojen parissa, pysykää kuulolla 🚀
.