Posted on

Faasi (aallot)

, Author

Värähtelyn tai aallon vaihe on se osa täydestä syklistä, joka vastaa siirtymän siirtymää tietystä vertailupisteestä ajanhetkellä t = 0. Vaihe on taajuusalueen tai Fourier-muunnosalueen käsite, ja sellaisena se voidaan helposti ymmärtää yksinkertaisen harmonisen liikkeen kannalta. Sama käsite pätee aaltoliikkeeseen, jota tarkastellaan joko pisteessä avaruudessa tietyn ajanjakson aikana tai avaruuden poikki tietyllä ajanhetkellä. Yksinkertainen harmoninen liike on siirtymä, joka vaihtelee syklisesti, kuten alla on kuvattu:

File:Simple harmonic motion.png

ja kuvataan kaavalla:

{\displaystyle x(t)=A\cdot \sin(2\pi ft+\theta ),\,}

jossa A on värähtelyn amplitudi, f on taajuus, t on kulunut aika ja {\displaystyle \theta } on värähtelyn vaihe. Vaihe määrää tai määräytyy alkusiirtymän perusteella hetkellä t = 0. Liikkeellä, jonka taajuus on f, on jakso {\displaystyle T={\frac {1}{f}}}.}

Voidaan huomata kaksi mahdollista epäselvyyttä:

  • Yksi on se, että alkusiirtymä {\displaystyle \cos(2\pi ft+\theta )\,} on erilainen kuin sinifunktio, mutta silti näyttäisi siltä, että niillä on sama ”vaihe”.
  • Aikavaihtelukulmaa {\displaystyle 2\pi ft+\theta ,\,} tai sen modulo {\displaystyle 2\pi } arvoa kutsutaan yleisesti myös ”vaiheeksi”. Silloin se ei ole alkuehto, vaan jatkuvasti muuttuva tila.

Termiä hetkellinen vaihe käytetään erottamaan ajassa muuttuva kulma alkuehdosta. Sillä on myös muodollinen määritelmä, joka soveltuu yleisempiin funktioihin ja määrittelee yksiselitteisesti funktion alkuvaiheen hetkellä t=0. Esim. sinillä ja kosinuksella on luonnostaan erilaiset alkuvaiheet. Ellei nimenomaisesti toisin mainita, kosinus on yleensä pääteltävä. (ks. myös faasori)

Vaiheensiirto

Tiedosto:Vaiheensiirto.png

Kuvitus vaiheensiirrosta. Vaaka-akseli edustaa kulmaa (vaihetta), joka kasvaa ajan myötä.

{\displaystyle \theta } kutsutaan joskus vaihesiirtymäksi, koska se edustaa ”siirtymää” nollavaiheesta. Mutta muutosta {\displaystyle \theta } kutsutaan myös vaiheensiirtymäksi.

Jos kyseessä on äärettömän pitkä sinusoidi, muutos {\displaystyle \theta } on sama kuin siirtymä ajassa, kuten aikaviive. Jos {\displaystyle x(t)\,} viivytetään (aikasiirretään) {\displaystyle {\begin{matrix}{\frac {1}{4}}}\end{matrix}}\,} sen syklin verran, siitä tulee:

{\displaystyle x(t-{\begin{matrix}{\frac {1}{4}}\end{matrix}}}T)\,} {\displaystyle =A\cdot \sin(2\pi f(t-{\begin{matrix}{\frac {1}{4}}}\end{matrix}}T)+\theta )\,}
{\displaystyle =A\cdot \sin(2\pi ft-{\begin{matrix}{\frac {\pi }{2}}\end{matrix}}+\theta ),\,}

jonka ”vaihe” on nyt {\displaystyle \theta -{\begin{matrix}{\frac {\pi }{2}}\end{matrix}}}.} Se on siirtynyt {\displaystyle {\begin{matrix}{\frac {\pi }{2}}\end{matrix}}}.

Vaihe-ero

Tiedosto:Siniaallot sama vaihe.svg

Vaiheessa olevat aallot

Tiedosto:Siniaallot eri vaihe.svg

Vaiheessa olevat aallot

Tiedosto:Vaiheensiirto havainnollistus.png

Vasemmalla: ylhäältä alaspäin kulkevan tasoaallon reaaliosa. Oikealla: sama aalto sen jälkeen, kun keskiosaan on tehty vaihesiirto esimerkiksi kulkemalla lasin läpi, jonka paksuus on erilainen kuin muiden osien. (Oikeanpuoleisessa kuvassa ei oteta huomioon diffraktiovaikutusta, jonka vaikutus kasvaa suurilla etäisyyksillä).

Kahdella oskillaattorilla, joilla on sama taajuus ja eri vaiheet, on vaihe-ero, ja oskillaattoreiden sanotaan olevan vaiheesta poissa keskenään. Määrä, jolla tällaiset oskillaattorit ovat keskenään epäkeskeisiä, voidaan ilmaista asteina välillä 0°-360° tai radiaaneina välillä 0-2π. Jos vaihe-ero on 180 astetta (π radiaania), kahden oskillaattorin sanotaan olevan vastavaiheessa. Jos kaksi vuorovaikutuksessa olevaa aaltoa kohtaavat pisteessä, jossa ne ovat vastavaiheessa, syntyy destruktiivinen interferenssi. On tavallista, että sähkömagneettisen (valo, RF), akustisen (ääni) tai muun energian aallot asettuvat päällekkäin siirtovälineessä. Tällöin vaihe-ero ratkaisee, vahvistavatko vai heikentävätkö ne toisiaan. Täydellinen kumoaminen on mahdollista aalloille, joiden amplitudit ovat yhtä suuret.

Aikaa käytetään joskus (kulman sijasta) ilmaisemaan sijaintia värähtelyn syklissä.

  • Vaihe-ero on verrattavissa siihen, että kaksi urheilijaa juoksee kilparadalla samaa vauhtia ja samaan suuntaan, mutta lähtee liikkeelle eri kohdista rataa. He ohittavat pisteen eri ajanhetkillä. Mutta heidän välinen aikaero (vaihe-ero) on vakio – sama jokaisessa ohituksessa, koska he kulkevat samalla nopeudella ja samaan suuntaan. Jos ne olisivat eri nopeuksilla (eri taajuuksilla), vaihe-ero heijastaisi vain eri lähtöasemia.
  • Me mittaamme maapallon pyörimistä tunteina eikä radiaaneina. Ja siksi aikavyöhykkeet ovat esimerkki vaihe-eroista.

In-vaihe- ja kvadratuurikomponentit (I&Q)

Termi in-vaihe esiintyy myös tietoliikennesignaalien yhteydessä:

{\displaystyle A(t)\cdot \sin=I(t)\cdot \sin(2\pi ft)+Q(t)\cdot {\cos(2\pi ft)} {\cos(2\pi ft)} _{\sin \left(2\pi ft+{\begin{matrix}{\frac {\pi }{2}}\end{matrix}}\right)}}

ja:

{\displaystyle A(t)\cdot \cos=I(t)\cdot \cos(2\pi ft)\underbrace {-Q(t)\cdot \sin(2\pi ft)} _{+Q(t)\cdot \cos \left(2\pi ft+{\begin{matrix}{\frac {\pi }{2}}\end{matrix}}\right)}}

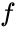
jossa {\displaystyle f\,} edustaa kantoaaltotaajuutta, ja

{\displaystyle I(t)\ {\stackrel {\mathrm {def} A(t)\cdot \cos,\,} {\displaystyle Q(t)\ {\stackrel {\mathrm {def} }{=}}\ A(t)\cdot \sin.\,}

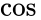
{\displaystyle A(t)\,} ja {\displaystyle \phi (t)\,} edustavat mahdollisia puhtaan kantoaallon modulaatioita, esim: {\displaystyle \sin(2\pi ft).\,} Modulaatio muuttaa kantoaallon alkuperäistä {\displaystyle \sin \,} -komponenttia ja luo (uuden) {\displaystyle \cos \,} -komponentin, kuten edellä on esitetty. Komponenttia, joka on samassa vaiheessa alkuperäisen kantoaallon kanssa, kutsutaan in-vaiheiseksi komponentiksi. Toista komponenttia, joka on aina 90° ({\displaystyle {\begin{matrix}{\frac {\pi }{2}}}\end{matrix}}} radiaania) ”pois vaiheesta”, kutsutaan kvadratuurikomponentiksi.

Vaihekoherenssi

Koherenssi on aallon ominaisuus osoittaa hyvin määriteltyä vaihesuhdetta sen määrittelyalueen eri alueilla.

Fysiikassa kvanttimekaniikka liittää aallot fysikaalisiin kohteisiin. Aaltofunktio on kompleksinen, ja koska sen neliömoduuli liittyy kohteen havaitsemisen todennäköisyyteen, aaltofunktion kompleksinen luonne liittyy vaiheeseen. Koska kompleksialgebra on vastuussa kvanttimekaniikan silmiinpistävästä interferenssi-ilmiöstä, hiukkasten vaihe liittyy näin ollen viime kädessä niiden kvanttikäyttäytymiseen.

Vastaa

Sähköpostiosoitettasi ei julkaista.