Tässä artikkelissa selitän, miten 2D-konvoluutiot toteutetaan matriisikertoina. Tämä selitys perustuu CS231n Convolutional Neural Networks for Visual Recognition (moduuli 2) -kurssin muistiinpanoihin. Oletan, että lukija tuntee konvoluutio-operaation käsitteen syvän neuroverkon yhteydessä. Jos ei, tässä repossa on raportti ja erinomaisia animaatioita, joissa selitetään, mitä konvoluutiot ovat. Koodin, jolla toistetaan tässä artikkelissa esitetyt laskutoimitukset, voi ladata täältä.
Pieni esimerkki
Esitellään, että meillä on yksikanavainen 4 x 4 kuva, X, ja sen pikseliarvot ovat seuraavat:

Esitellään lisäksi, että määritetään 2D-taajuinen konvoluutio seuraavilla ominaisuuksilla:

Tämähän tarkoittaa sitä, että on olemassa yhdeksän 2 x 2 -kuva-aluetta (patches), jotka elementtiviisaana kerrotaan matriisilla W, näin:

Nämä kuvalaikut voidaan esittää 4-ulotteisina sarakevektoreina ja ketjuttaa yhdeksi 4 x 9 matriisiksi, P, seuraavasti:

Huomaa, että matriisin P i:nneksi viimeinen sarake on itse asiassa i:nneksi viimeinen kuvapatsaan sarakevektori.
Konvoluutiokerroksen painojen matriisi, W, voidaan litistää 4-ulotteiseksi rivivektoriksi , K, seuraavasti:
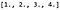
Toteuttaaksemme konvoluution kerromme ensin matriisikertoimen K:n ja P:n välillä, jolloin saamme 9-ulotteisen rivivektorin (1 x 9-matriisin), joka antaa:

Sitten muokkaamme K P:n tuloksen oikeaan muotoon, joka on 3 x 3 x 1 -matriisi (kanavan ulottuvuus viimeinen). Kanavaulottuvuus on 1, koska asetimme lähtösuodattimet arvoon 1. Korkeus ja leveys on 3, koska CS231n muistiinpanojen mukaan:

Tämä tarkoittaa, että konvoluution tulos on:
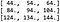
Joka tarkistetaan, jos suoritamme konvoluution PyTorchin sisäänrakennetuilla funktioilla (katso tarkemmin tämän artikkelin oheiskoodista).
Lisäesimerkki
Edellisen kappaleen esimerkissä oletetaan, että kyseessä on yksi kuva ja konvoluution ulostulokanavat ovat 1. Mikä muuttuisi, jos höllentäisimme näitä oletuksia?
Emme oleta, että konvoluution syötteenä on 4 x 4-kanavainen kuva, jossa on 3 kanavaa, joiden pikseliarvot ovat seuraavat:

Konvoluutiossamme asetamme sen samoiksi ominaisuuksiksi kuin edellisessä osiossa lukuun ottamatta sitä, että sen ulostulosuodattimet ovat 2. Tämä tarkoittaa, että alkuperäisen painomatriisin, W, on oltava muodoltaan (2, 2, 2, 2, 3) eli (lähtösuodattimet, ytimen korkeus, ytimen leveys, tulokuvan kanavat). Asetetaan W:lle seuraavat arvot:

Huomaa, että jokaisella ulostulosuodattimella on oma ytimensä (siksi meillä on tässä esimerkissä 2 ydintä) ja jokaisen ytimen kanava on 3 (koska sisääntulokuvassa on 3 kanavaa).
Koska edelleen konvoluoimme 2 x 2 ytimen 4 x 4-kuvaan, jossa on nollatäytteisyys 0 ja stride 1, kuvapatsaiden määrä on edelleen 9. Kuvalappujen matriisi P on kuitenkin erilainen. Tarkemmin sanottuna P:n i:s sarake on 1., 2. ja 3. kanavan arvojen ketjutus (sarakevektorina), jotka vastaavat kuvalaattaa i. P on nyt 12 x 9-kokoinen matriisi. Rivejä on 12, koska kullakin kuvalaatikolla on 3 kanavaa ja kullakin kanavalla on 4 elementtiä, koska asetimme ytimen kooksi 2 x 2. Näin P näyttää:

Kuten W:n kohdalla, kukin kernel litistetään rivivektoriksi ja ketjutetaan riveittäin, jotta saadaan muodostettua 2 x 12-matriisi K. K:n i:s rivi on i:ttä ydintä vastaavien 1., 2. ja 3. kanava-arvojen ketjutus (rivivektorina). Seuraavalta K näyttää:

Nyt jäljellä on enää matriisikertolaskennan K P suorittaminen ja sen muokkaaminen oikeaan muotoon. Oikea muoto on 3 x 3 x 2 -matriisi (kanavan ulottuvuus viimeisenä). Tässä on kertolaskun tulos:

Ja tässä on tulos sen jälkeen, kun se on muotoiltu uudestaan 3x3x3x2-matriisiksi:

Joka taasen tarkistetaan, jos suoritamme konvoluution PyTorchin sisäänrakennetuilla funktioilla (ks. tarkemmat yksityiskohdat tämän artikkelin oheiskoodista).
So What?
Miksi meidän pitäisi välittää 2D-konvoluutioiden ilmaisemisesta matriisien kertolaskuina? Sen lisäksi, että meillä on tehokas toteutus, joka soveltuu GPU:lla suoritettavaksi, tämän lähestymistavan tunteminen antaa meille mahdollisuuden järkeillä syvän konvoluutiohermoverkon käyttäytymistä. Esimerkiksi He et. al. (2015) ilmaisivat 2D-konvoluutiot matriisikertojen avulla, minkä ansiosta he pystyivät soveltamaan satunnaismatriisien/vektoreiden ominaisuuksia argumentoidakseen paremman painojen alustamisrutiinin puolesta.
Johtopäätös
Tässä artikkelissa olen selittänyt, miten 2D-konvoluutiot suoritetaan matriisikertojen avulla käymällä läpi kaksi pientä esimerkkiä. Toivon, että tämä riittää sinulle yleistettäväksi mielivaltaisiin tulokuvan dimensioihin ja konvoluutio-ominaisuuksiin. Kerro minulle kommenteissa, jos jokin on epäselvää.
1D-konvoluutio
Tässä artikkelissa kuvattu menetelmä yleistyy myös 1D-konvoluutioihin.
Esitellään esimerkiksi, että syötteesi on 3-kanavainen 12-ulotteinen vektori seuraavasti:

Jos asetamme 1D-konvoluutiollemme seuraavat parametrit:
- kernel size: 1 x 4
- output channels: 2
- stride: 2
- padding: 0
- bias: 0
Tällöin konvoluutio-operaation parametrit, W, ovat tensori, jonka muoto on (2 , 3, 1, 4). Asetetaan W:lle seuraavat arvot:

Konvoluutio-operaation parametrien perusteella ”kuva”-laikkujen matriisi P, on muodoltaan (12, 5) (5 kuvalaikkua, jossa kukin kuvalaikka on 12-D vektori, koska laikulla on 4 elementtiä kolmessa kanavassa) ja se näyttää seuraavalta:

Seuraavaksi litistämme W:n saadaksemme K:n, joka on muodoltaan (2, 12), koska kuvakeskittymiä (kerneleitä) on kaksi, ja kullakin kernelillä on 12 elementtiä. Tältä K näyttää:

Nyt voimme kertoa K:n P:llä, jolloin saadaan:

Viimeiseksi muokkaamme K P:n oikeaan muotoon, joka kaavan mukaan on ”kuva”, jonka muoto on (1, 5). Tämä tarkoittaa, että tämän konvoluution tulos on tensori, jonka muoto on (2, 1, 5), koska asetimme lähtökanaviksi 2. Tältä lopputulos näyttää:

Joka odotetusti tarkistetaan, jos suorittaisimme konvoluution PyTorchin sisäänrakennetuilla funktioilla.