Luokittelu on valvottu koneoppimismenetelmä, jossa algoritmi oppii sille annetusta syötetystä datasta – ja käyttää sitten tätä oppimista uusien havaintojen luokitteluun.
Muilla sanoilla, koulutustietokokonaisuutta käytetään parempien reunaehtojen hankkimiseen, joita voidaan käyttää kunkin kohdeluokan määrittelyyn; kun tällaiset reunaehdot on saatu määriteltyä, seuraavana tehtävänä on ennustaa kohdeluokka.
Binääriluokittelijat työskentelevät vain kahden luokan tai mahdollisen lopputuloksen kanssa (esimerkki: positiivinen tai negatiivinen tunne; maksaako lainanantaja lainan vai ei; jne.), ja moniluokkaiset luokittelijat työskentelevät useiden luokkien kanssa (esimerkki: mihin maahan lippu kuuluu, onko kuva omena vai banaani vai appelsiini; jne.). Multiclass-luokittelussa oletetaan, että jokaiselle näytteelle annetaan yksi ja vain yksi etiketti.

Yksi ensimmäisistä suosituista luokittelualgoritmeista koneellisessa oppimisessa oli Naive Bayes, Bayesin teoreeman innoittama todennäköisyysluokittelija (jonka avulla voimme tehdä perusteltuja päätelmiä reaalimaailmassa tapahtuvista tapahtumista perustuen aiempaan tietämykseen havainnoista, jotka saattavat viitata siihen). Nimi (”Naive”) juontaa juurensa siitä, että algoritmi olettaa attribuuttien olevan ehdollisesti riippumattomia.
Algoritmi on yksinkertainen algoritmi toteuttaa, ja se on yleensä kohtuullinen menetelmä luokittelupyrkimysten käynnistämiseksi. Se voidaan helposti skaalata suuremmille tietokokonaisuuksille (vie lineaarisen ajan verrattuna iteratiiviseen approksimaatioon, jota käytetään monissa muuntyyppisissä luokittelijoissa ja joka on kalliimpaa laskentaresurssien kannalta) ja vaatii pienen määrän harjoitusdataa.
Naiivi Bayes voi kuitenkin kärsiä ongelmasta, joka tunnetaan nimellä ”nollatodennäköisyysongelma”, kun ehdollinen todennäköisyys on nolla tietylle attribuutille, jolloin kelvollista ennustetta ei voida antaa. Yksi ratkaisu on hyödyntää tasoitusmenettelyä (esim. Laplace-menetelmä).

P(c|x) on posteriorinen todennäköisyys luokalle (c, kohde), kun otetaan huomioon prediktor (x, attribuutit). P(c) on luokan ennakkotodennäköisyys. P(x|c) on todennäköisyys (likelihood), joka on ennustajan todennäköisyys luokka annettuna, ja P(x) on ennustajan ennakkotodennäköisyys.
Algoritmin ensimmäisessä vaiheessa on kyse ennakkotodennäköisyyden laskemisesta annetuille luokkatunnisteille. Sen jälkeen etsitään todennäköisyystodennäköisyys kullakin attribuutilla kullekin luokalle. Tämän jälkeen laitetaan nämä arvot Bayesin kaavaan & lasketaan posteriorinen todennäköisyys, ja sitten katsotaan, kummalla luokalla on suurempi todennäköisyys, kun syötteen annetaan kuuluvan korkeamman todennäköisyyden luokkaan.
Naive Bayesin toteuttaminen Pythonissa on melko suoraviivaista scikit-learn-kirjastoa hyödyntäen. Itse asiassa scikit-learn-kirjaston alla on kolmenlaisia Naive Bayes -malleja: (a) Gaussin tyyppi (olettaa, että ominaisuudet noudattavat kellon kaltaista normaalijakaumaa), (b) Multinomiaalinen (käytetään diskreetteihin lukumääriin, eli siihen, kuinka monta kertaa lopputulos havaitaan x:n kokeilun aikana) ja (c) Bernoulli (hyödyllinen binäärisille ominaisuusvektoreille; suosittu käyttötapaus on tekstiluokittelu).
Toinen suosittu mekanismi on päätöspuu. Kun annetaan attribuutteja sisältävä data ja sen luokat, puu tuottaa sarjan sääntöjä, joita voidaan käyttää datan luokitteluun. Algoritmi jakaa otoksen kahteen tai useampaan homogeeniseen joukkoon (lehtiin) tulomuuttujien merkittävimpien erottajien perusteella. Erottajan (ennustajan) valitsemiseksi algoritmi tarkastelee kaikkia piirteitä ja tekee niille binäärisen jaon (kategoristen tietojen osalta jako kategorian mukaan; jatkuvien tietojen osalta valitaan rajauskynnys). Sitten se valitsee sen, jolla on vähiten kustannuksia (eli suurin tarkkuus), ja toistaa rekursiivisesti, kunnes se onnistuu jakamaan datan kaikissa lehdissä (tai saavuttaa maksimisyvyyden).
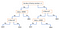
Päätöksentekopuiden ymmärtäminen ja havainnollistaminen sujuu yleensä helposti, ja ne vaativat vain vähän datan esivalmistelua. Tällä menetelmällä voidaan myös käsitellä sekä numeerista että kategorista dataa. Toisaalta monimutkaiset puut eivät yleisty hyvin (”ylisovittaminen”), ja päätöspuut voivat olla jossain määrin epävakaita, koska pienetkin vaihtelut datassa saattavat johtaa täysin erilaisen puun tuottamiseen.
Päätöspuista johdettu luokittelumenetelmä on Random Forest, joka on pohjimmiltaan ”meta-estimaattori”, joka sovittaa useita päätöspuita erilaisiin datajoukkojen osaotoksiin ja käyttää keskiarvoja parantaakseen mallin ennustetarkkuutta ja hillitäkseen ylisovittamista. Osaotosten koko on sama kuin alkuperäisen syöttöotoksen koko – mutta otokset poimitaan korvaavasti.
Sattumanvaraisilla metsillä on taipumus osoittaessaan korkeampaa robustisuutta ylisovittamista vastaan (>robustisuus datan kohinaa kohtaan), ja niiden suoritusaika on tehokas myös suuremmissa datajoukoissa. Ne ovat kuitenkin herkempiä epätasapainoisille tietokokonaisuuksille, mutta niiden tulkinta on myös hieman monimutkaisempaa ja ne vaativat enemmän laskentaresursseja.
Toinen suosittu luokittelija ML:ssä on logistinen regressio – jossa yksittäisen kokeen mahdollisia tuloksia kuvaavia todennäköisyyksiä mallinnetaan logistisella funktiolla (luokittelumenetelmä nimestä huolimatta):
Tältä logistinen yhtälö näyttää:
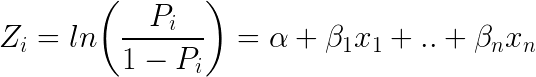
Valitsemalla e (eksponentti) yhtälön molemmille puolille saadaan:
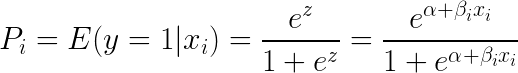
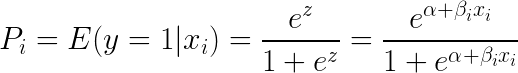
Logistinen regressio on käyttökelpoisin, kun halutaan ymmärtää usean riippumattoman muuttujan vaikutusta yksittäiseen tulosmuuttujaan. Se keskittyy binääriseen luokitteluun (ongelmiin, joissa on useita luokkia, käytetään logistisen regression laajennuksia, kuten multinomiaalista ja ordinaalista logistista regressiota). Logistinen regressio on suosittu useissa käyttötapauksissa, kuten luottoanalyysissä ja reagointi-/ostohalukkuudessa.
Viimeiseksi, mutta ei vähäisimpänä, kNN:ää (lyhenne sanoista ”k Nearest Neighbors”, eli ”k lähintä naapuria”) käytetään myös usein luokitusongelmissa. kNN on yksinkertainen algoritmi, joka tallentaa kaikki saatavilla olevat tapaukset ja luokittelee uudet tapaukset samankaltaisuusmittarin (esim. etäisyysfunktioiden) perusteella. Sitä on käytetty tilastollisessa estimoinnissa ja hahmontunnistuksessa jo 1970-luvun alussa ei-parametrisena tekniikkana:

