Esittely

Kuvittele tämä – Sinulle on annettu tehtäväksi ennustaa seuraavan iPhonen hintaa, ja sinulle on toimitettu historiallisia tietoja. Tämä sisältää ominaisuuksia, kuten neljännesvuosimyyntiä, kuukausittaisia menoja ja koko joukon asioita, jotka kuuluvat Applen taseeseen. Minkälaiseksi ongelmaksi luokittelisit tämän datatieteilijänä? Aikasarjamallinnus, tietenkin.

Tuotteen myynnin ennustamisesta kotitalouksien sähkönkäytön arviointiin, aikasarjojen ennustaminen on yksi keskeisistä taidoista, jotka jokaisen datatieteilijän odotetaan osaavan, ellei jopa hallitsevan. On olemassa lukuisia erilaisia tekniikoita, joita voit käyttää, ja käsittelemme tässä artikkelissa yhtä tehokkaimmista, nimeltään Auto ARIMA.

Ymmärrämme ensin ARIMA:n käsitteen, joka johdattaa meidät pääaiheeseemme – Auto ARIMA:han. Käsitteidemme vakiinnuttamiseksi otamme käyttöön tietokokonaisuuden ja toteutamme sen sekä Pythonilla että R:llä.

Sisällysluettelo

1. Mikä on aikasarja?
2. Aikasarjojen ennustamisen menetelmät
3. Esittely ARIMA:an
4. Vaiheet ARIMA:n toteuttamiseen
5. Mihin tarvitsemme AutoARIMA:aa?
6. Auto ARIMA -toteutus (lentomatkustajien aineistolla)
7. Miten auto ARIMA valitsee parametrit?

Jos olet perehtynyt aikasarjoihin ja niiden tekniikoihin (kuten liukuvaan keskiarvoon, eksponentiaaliseen tasoitukseen ja ARIMA:han), voit siirtyä suoraan kohtaan 4. Aloittelijoille, aloita alla olevasta osiosta, joka on lyhyt johdatus aikasarjoihin ja erilaisiin ennustetekniikoihin.

Mikä on aikasarja?

Ennen kuin opimme aikasarjadatan työstämisessä käytettäviä tekniikoita, meidän on ensin ymmärrettävä, mikä aikasarja oikeastaan on ja miten se eroaa muista datatyypeistä. Tässä on aikasarjan muodollinen määritelmä – Se on sarja datapisteitä, jotka on mitattu tasaisin aikavälein. Tämä tarkoittaa yksinkertaisesti sitä, että tietyt arvot tallennetaan tasaisin väliajoin, jotka voivat olla tuntikohtaisia, päivittäisiä, viikoittaisia, 10 päivän välein ja niin edelleen. Aikasarjasta tekee erilaisen se, että sarjan jokainen datapiste on riippuvainen edellisistä datapisteistä. Ymmärrämme eron selkeämmin parin esimerkin avulla.

Esimerkki 1:

Esitetään, että sinulla on tietokokonaisuus ihmisistä, jotka ovat ottaneet lainaa tietystä yrityksestä (kuten alla olevassa taulukossa). Luuletko, että jokainen rivi liittyy edellisiin riveihin? Ei varmastikaan! Henkilön ottama laina perustuu hänen taloudellisiin olosuhteisiinsa ja tarpeisiinsa (voi olla muitakin tekijöitä, kuten perheen koko jne., mutta yksinkertaisuuden vuoksi tarkastelemme vain tuloja ja lainatyyppiä) . Tietoja ei myöskään kerätty millään tietyllä ajanjaksolla. Se riippuu siitä, milloin yritys sai lainahakemuksen.

Esimerkki 2:

Katsotaanpa toinen esimerkki. Oletetaan, että sinulla on tietokokonaisuus, joka sisältää ilman hiilidioksidipitoisuuden vuorokaudessa (kuvakaappaus alla). Pystytkö ennustamaan CO2:n likimääräisen määrän seuraavalle päivälle tarkastelemalla viime päivien arvoja? Totta kai. Jos huomaat, tiedot on tallennettu päivittäin, eli aikaväli on vakio (24 tuntia).

Olet varmaan jo saanut tästä intuition – ensimmäinen tapaus on yksinkertainen regressio-ongelma ja toinen aikasarja-ongelma. Tosin aikasarja-ongelma tässä voidaan ratkaista myös lineaarisella regressiolla, mutta se ei oikeastaan ole paras lähestymistapa, koska siinä jätetään huomiotta arvojen suhde kaikkiin suhteellisiin menneisiin arvoihin. Tarkastellaan nyt joitakin yleisiä tekniikoita, joita käytetään aikasarja-ongelmien ratkaisemiseen.

Aikasarjojen ennustamiseen käytettävät menetelmät

Aikasarjojen ennustamiseen on olemassa useita menetelmiä, ja käsittelemme niitä lyhyesti tässä jaksossa. Yksityiskohtainen selitys ja python-koodit kaikille alla mainituille tekniikoille löytyvät tästä artikkelista: 7 tekniikkaa aikasarjan ennustamiseen (python-koodeilla).

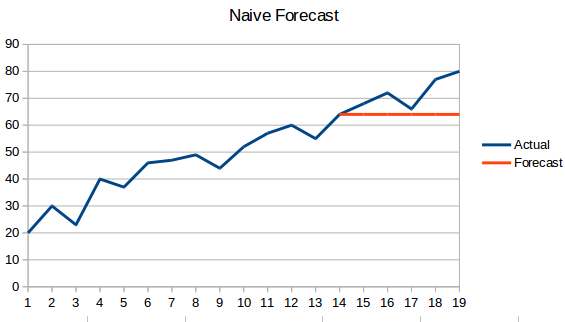
1. Naivistinen lähestymistapa: Tässä ennustustekniikassa uuden datapisteen arvon ennustetaan olevan yhtä suuri kuin edellisen datapisteen arvo. Tuloksena olisi tasainen viiva, koska kaikki uudet arvot ottavat edelliset arvot.
2. Yksinkertainen keskiarvo: Seuraava arvo otetaan kaikkien edellisten arvojen keskiarvona. Ennusteet ovat tässä tapauksessa paremmat kuin ”naiivissa lähestymistavassa”, koska tuloksena ei ole tasainen viiva, mutta tässä tapauksessa kaikki aiemmat arvot otetaan huomioon, mikä ei välttämättä ole aina hyödyllistä. Kun esimerkiksi pyydetään ennustamaan tämän päivän lämpötilaa, otetaan huomioon viimeisten 7 päivän lämpötila eikä kuukauden takaista lämpötilaa.
3. Liukuva keskiarvo : Tämä on parannus edelliseen tekniikkaan verrattuna. Sen sijaan, että otettaisiin kaikkien aikaisempien pisteiden keskiarvo, otetaan ennustetuksi arvoksi ’n’ aikaisemman pisteen keskiarvo.
4. Painotettu liukuva keskiarvo : Painotettu liukuva keskiarvo on liukuva keskiarvo, jossa aikaisemmille ’n’ arvolle annetaan eri painoarvot.
5. Yksinkertainen eksponentiaalinen tasoitus : Tässä tekniikassa annetaan suuremmat painot tuoreemmille havainnoille kuin kaukaisemman menneisyyden havainnoille.
6. Holtin lineaarinen trendimalli: Tässä menetelmässä otetaan huomioon aineiston trendi. Trendillä tarkoitetaan sarjan kasvavaa tai laskevaa luonnetta. Oletetaan, että hotellin varausten määrä kasvaa joka vuosi, niin voidaan sanoa, että varausten määrässä on kasvava trendi. Tässä menetelmässä ennustefunktio on tason ja trendin funktio.
7. Holt Wintersin menetelmä: Tämä algoritmi ottaa huomioon sekä sarjan trendin että kausivaihtelun. Esimerkiksi – hotellivarausten määrä on suuri viikonloppuisin & pieni arkipäivisin ja kasvaa joka vuosi; on olemassa viikoittainen kausivaihtelu ja kasvava trendi.
8. ARIMA: ARIMA on hyvin suosittu tekniikka aikasarjojen mallintamiseen. Se kuvaa datapisteiden välistä korrelaatiota ja ottaa huomioon arvojen erotuksen. ARIMA:n parannus on SARIMA (tai kausittainen ARIMA). Tarkastelemme ARIMAa hieman yksityiskohtaisemmin seuraavassa osiossa.

Esittely ARIMAan

Tässä osiossa teemme nopean johdannon ARIMAan, josta on apua Auto Ariman ymmärtämisessä. Yksityiskohtainen selitys Arimasta, parametreista (p,q,d), kuvaajista (ACF PACF) ja toteutuksesta sisältyy tähän artikkeliin :

ARIMA on erittäin suosittu tilastollinen menetelmä aikasarjan ennustamiseen. ARIMA tulee sanoista Auto-Regressive Integrated Moving Averages. ARIMA-mallit toimivat seuraavilla oletuksilla –

• Datasarja on stationaarinen, mikä tarkoittaa, että keskiarvo ja varianssi eivät saisi vaihdella ajan myötä. Sarjasta voidaan tehdä stationaarinen käyttämällä log-muunnosta tai differentioimalla sarja.
• Syötteenä annettavan datan on oltava yksimuuttujainen sarja, koska ARIMA käyttää menneitä arvoja ennustamaan tulevia arvoja.

ARIMA:ssa on kolme komponenttia – AR (autoregressiivinen termi), I (differentiointitermi) ja MA (liukuvan keskiarvon termi). Ymmärretään jokainen näistä komponenteista –

• AR-termi viittaa menneisiin arvoihin, joita käytetään seuraavan arvon ennustamiseen. AR-termi määritellään parametrilla ’p’ arimassa. ’p:n’ arvo määritetään PACF-diagrammin avulla.
• MA-termiä käytetään määrittelemään tulevien arvojen ennustamiseen käytettyjen menneiden ennustevirheiden määrä. Parametri ’q’ arimassa edustaa MA-termiä. ACF-diagrammia käytetään oikean ’q’-arvon määrittämiseen.
• Differentioinnin järjestys määrittää, kuinka monta kertaa sarjalle suoritetaan differentiointioperaatio, jotta se saadaan pysyväksi. ADF:n ja KPSS:n kaltaisia testejä voidaan käyttää sen määrittämiseen, onko sarja stationaarinen, ja ne auttavat d-arvon tunnistamisessa.

Vaiheet ARIMA-mallin toteuttamiseen

Yleiset vaiheet ARIMA-mallin toteuttamiseen ovat: –

1. Lataa data: Mallin rakentamisen ensimmäinen vaihe on luonnollisesti aineiston lataaminen
2. Esikäsittely: Aineistosta riippuen määritellään esikäsittelyn vaiheet. Siihen kuuluu aikaleimojen luominen, päivämäärä/aika-sarakkeen d-tyypin muuntaminen, sarjan muuttaminen yksimuuttujalliseksi jne.
3. Sarjan muuttaminen pysyväksi: Jotta oletus täyttyisi, sarjasta on tehtävä stationaarinen. Tähän kuuluu sarjan stationaarisuuden tarkistaminen ja tarvittavien muunnosten suorittaminen
4. Määritä d-arvo: Jotta sarja saataisiin stationaariseksi, d-arvona pidetään sitä, kuinka monta kertaa erotusoperaatio on suoritettu
5. Luodaan ACF- ja PACF-diagrammit: Tämä on tärkein vaihe ARIMA-toteutuksessa. ACF PACF-plotteja käytetään ARIMA-mallimme syöttöparametrien määrittämiseen
6. Määritä p- ja q-arvot: Lue p:n ja q:n arvot edellisen vaiheen kuvaajista
7. Sovita ARIMA-malli: Sovita ARIMA-malli käyttäen käsiteltyjä tietoja ja edellisissä vaiheissa laskemiamme parametriarvoja
8. Ennusta arvot validointijoukosta: Ennustetaan tulevat arvot
9. Lasketaan RMSE: Mallin suorituskyvyn tarkistamiseksi tarkistetaan RMSE-arvo käyttämällä validointijoukon ennusteita ja todellisia arvoja

Miksi tarvitsemme Auto ARIMA:a?

Vaikka ARIMA on erittäin tehokas malli aikasarjadatan ennustamiseen, datan valmistelu- ja parametrin virittämisprosessit ovat lopulta todella aikaa vieviä. Ennen ARIMA:n toteuttamista sarjasta on tehtävä stationaarinen ja määritettävä p:n ja q:n arvot edellä käsittelemiemme kuvaajien avulla. Auto ARIMA tekee tästä tehtävästä meille todella yksinkertaisen, koska se poistaa edellisessä jaksossa näkemämme vaiheet 3-6. Seuraavassa on vaiheet, joita sinun tulisi noudattaa auto ARIMA:n toteuttamiseksi:

1. Load the data: Tämä vaihe on sama. Lataa data muistikirjaasi
2. Datan esikäsittely: Syötteen tulee olla yksimuuttujainen, joten pudota muut sarakkeet
3. Fit Auto ARIMA: Sovita malli yksimuuttujaiselle sarjalle
4. Predict values on validation set: Tee ennusteet validointijoukolle
5. Calculate RMSE: Tarkista mallin suorituskyky käyttämällä ennustettuja arvoja todellisia arvoja vastaan

Olemme ohittaneet kokonaan p- ja q-ominaisuuden valinnan, kuten näet. Mikä helpotus! Seuraavassa osiossa toteutamme automaattisen ARIMA-mallin käyttäen lelutietokokonaisuutta.

Toteutus Pythonilla ja R:llä

Käytämme International-Air-Passenger -tietokokonaisuutta. Tämä tietokokonaisuus sisältää matkustajien kuukausittaisen kokonaismäärän (tuhansina). Siinä on kaksi saraketta – kuukausi ja matkustajien lukumäärä. Voit ladata datasetin tästä linkistä.

#load the datadata = pd.read_csv('international-airline-passengers.csv')#divide into train and validation settrain = datavalid = data#preprocessing (since arima takes univariate series as input)train.drop('Month',axis=1,inplace=True)valid.drop('Month',axis=1,inplace=True)#plotting the datatrain.plot()valid.plot()

#building the modelfrom pyramid.arima import auto_arimamodel = auto_arima(train, trace=True, error_action='ignore', suppress_warnings=True)model.fit(train)forecast = model.predict(n_periods=len(valid))forecast = pd.DataFrame(forecast,index = valid.index,columns=)#plot the predictions for validation setplt.plot(train, label='Train')plt.plot(valid, label='Valid')plt.plot(forecast, label='Prediction')plt.show()

#calculate rmsefrom math import sqrtfrom sklearn.metrics import mean_squared_errorrms = sqrt(mean_squared_error(valid,forecast))print(rms)

output -76.51355764316357

Alhaalla on R-koodi samalle ongelmalle:

# loading packageslibrary(forecast)library(Metrics)# reading datadata = read.csv("international-airline-passengers.csv")# splitting data into train and valid setstrain = datavalid = data# removing "Month" columntrain$Month = NULL# training modelmodel = auto.arima(train)# model summarysummary(model)# forecastingforecast = predict(model,44)# evaluationrmse(valid$International.airline.passengers, forecast$pred)

Miten Auto Arima valitsee parhaat parametrit

Ylläolevassa koodissa käytimme yksinkertaisesti .fit()-käskyä mallin sovittamiseen ilman, että tarvitsisi valita yhdistelmää p, q, d. Mutta miten malli selvitti näiden parametrien parhaan yhdistelmän? Auto ARIMA ottaa huomioon tuotetut AIC- ja BIC-arvot (kuten koodissa näkyy) määrittääkseen parhaan parametrien yhdistelmän. AIC- (Akaike Information Criterion) ja BIC- (Bayesian Information Criterion) arvot ovat estimaattoreita, joiden avulla voidaan vertailla malleja. Mitä alhaisempia nämä arvot ovat, sitä parempi malli on.

Katso nämä linkit, jos olet kiinnostunut AIC:n ja BIC:n taustalla olevasta matematiikasta.

Loppuhuomautukset ja jatkolukemista

Olen havainnut auto ARIMA:n olevan yksinkertaisin tekniikka aikasarjojen ennustamiseen. Oikopolun tunteminen on hyvä, mutta sen taustalla olevan matematiikan tunteminen on myös tärkeää. Tässä artikkelissa olen käynyt lyhyesti läpi yksityiskohtia siitä, miten ARIMA toimii, mutta varmista, että käyt läpi artikkelissa annetut linkit. Helpoksi referenssiksi tässä vielä linkit:

• A Comprehensive Guide for beginners to Time Series Forecast in Python
• Complete Tutorial to Time series in R
• 7 tekniikkaa aikasarjojen ennustamiseen (python-koodeilla)

Esittäisin, että kannattaa harjoitella sitä, mitä olemme oppineet tässä harjoitustehtävässä: Aikasarjojen harjoittelutehtävä. Voit myös suorittaa samasta harjoitusongelmasta luodun harjoittelukurssimme Aikasarjojen ennustaminen, joka antaa sinulle etumatkaa.