Posted on

Symmetriaelementtien ja symmetriaoperaatioiden symbolit

, Author

Acta Cryst. (1992). A48, 727-732

Loppuraportti Kansainvälisen kiteilyliiton symmetrian nomenklatuuria käsittelevästä ad-hoc-komiteasta*

P. M. DE WOLFF (puheenjohtaja), Meermanstraat 126, 2614 AM Delft, Alankomaat,

Y. BILLIET, Ecole Nationale d’Ingénieurs, BPW 3038 Sfax, Tunesië,

J. D. H. DONNAY, Geologisten tieteiden laitos, McGill University, 3450 University Street, Montreal, Kanada H3A 2A7,

W. FISCHER, Institut für Mineralogie, Petrologie und Kristallographie der Phillips-Universität, Lahnberge, D-3550 Marburg (Lahn), Saksa,

R. B. GALIULIN, Institute of Crystallography, Academy of Sciences of Russia, Leninsky Prospekt 59, Moscow 117333, Russia,

A. M. GLAZER, Clarendon Laboratory, Oxfordin yliopisto, Parks Road, Oxford OX1 3PU Englanti,

TH. HAHN, Institut für Kristallographie, RWTH, Templergraben 55, D-5100 Aachen, Saksa,

MARJORIE SENECHAL, Department of Mathematics, Smith College, Northampton, MA 01063, USA,

D. P. SHOEMAKER, kemian laitos, Oregon State University, OR 97331, USA,

H. WONDRATSCHEK, Institut für Kristallographie, Universität Karlsruhe, Kaiserstrasse 12, D-7500 Karlsruhe 1, Saksa,

A. J. C. WILSON (ex officio, IUCr Commission on International Tables), Crystallographic Data Centre, University Chemistry Laboratory, Lensfield Road, Cambridge CB2 1EW, England

JA S. C. ABRAHAMS (ex officio, IUCr Commission on Crystallographic Nomenclature), Department of Physics, Southern Oregon State College, 1250 Siskiyou Boulevard, Ashland, OR 97520-5047, USA

(Vastaanotettu 7.11.1991; hyväksytty 9.3.1992)

* Nimitetty 14.11.1984, muutettu 10.8.1987 Acta Cryst. (1979), A35, 1072. Loppuraportti, jonka IUCr:n kiteiden nomenklatuuritoimikunta hyväksyi 23. joulukuuta 1991 ja toimeenpaneva komitea 9. maaliskuuta 1992.

Abstract

Uusia tai uudelleen määriteltyjä painettuja symboleja ehdotetaan symmetriaelementtien hiljattain hyväksytyn uudelleenmäärittelyn valossa. Erityisesti e-kirjain kattaa tietyt liukutasot, joilla ei tähän asti ole ollut omaa symbolia, kuten ”joko a tai b” -nimiset liukutasot. Suositellaan e:n käyttöä viiden eri avaruusryhmän Hermann-Mauguin-symbolissa. Tasoon nähden samansuuntaisesti projisoituja e-tasoja varten ehdotetaan graafista symbolia, joka poistaa niiden nykyiseen nimitykseen liittyvän epäselvyyden. Kirjainta k ehdotetaan äskettäin määritellylle liukutasojen luokalle, jolla ei tähän asti ole ollut erityistä tunnusta. International Tables for Crystallography (1989), Vol. A (Dordrecht: Kluwer Academic Publishers) -julkaisun avaruusryhmäkuvauksissa käyttöön otettuja symmetriaoperaatioiden symboleja suositellaan käytettäväksi yleisesti, ja niihin on tehty muutoksia ainoastaan liukupintaheijastusten osalta.

Esittely

Vuonna 1980 nimitetty tilapäiskomitea, jonka tehtävänä oli tarkastella ”avaruusryhmien symmetriaoperaatioita ja symmetriaelementtejä koskevia nomenklatuuriongelmia”, on julkaissut kaksi raporttia otsikolla Nomenclature for Crystal Families, Bravais-Lattice Types and Arithmetic Classes (de Wolff et al., 1985) ja Definition of Symmetry Elements in Space Groups and Point Groups (de Wolff et al., 1989). Kuten vuoden 1989 raportissa todetaan, ainoa symmetriaoperaatioihin liittyvä avoin ongelma on sopivien symbolien valinta, koska käsite on selkeä. Alustava merkintätapa on otettu käyttöön International Tables for Crystallography -julkaisussa (1983, 1989), jäljempänä ITA83.

Symmetriaelementtien painetut symbolit

Symmetriaelementtien määritelmää, sellaisena kuin se on esitetty vuoden 1989 raportissa (de Wolff et al.), käytetään koko tässä raportissa. Tässä toistetaan olennainen sisältö:

Kullekin symmetriaoperaatiolle määritellään sen geometrinen elementti (taso, piste ja/tai viiva). Symmetriaelementti on tietyn avaruusryhmän yhden symmetriaoperaation geometrisen elementin yhdistelmä kaikkien niiden kyseisen avaruusryhmän symmetriaoperaatioiden joukkoon (jota kutsutaan `elementtijoukoksi’), joilla on sama geometrinen elementti.

Geometristen elementtien eksplisiittiset määritelmät ja niistä johtuvien symmetriaelementtien kuvaukset sekä niiden symbolit on esitetty taulukoissa 1 ja 2. (Nämä ovat identtiset vuoden 1989 raportin taulukoiden 1 ja 2 kanssa, lukuun ottamatta liukutasoja, ja ne toistetaan tässä täydellisyyden vuoksi, ks. jäljempänä). Kutakin symmetriaelementtiä edustaa symboli, joka koostuu kahdesta merkistä. Ensimmäinen merkki on suuraakkosin kirjoitettu E kaikille symmetriaelementeille. Se osoittaa, että symboli viittaa symmetriaelementtiin eikä esimerkiksi symmetriaoperaatioon. Jos tämä selviää jo asiayhteydestä, E:n voi jättää pois, esim. ”akseli 2” eikä ”akseli E2”.

Taulukko 1. Symmetriamerkki. Piste- ja avaruusryhmien symmetriaoperaatioiden geometriset elementit
Symmetriaoperaatio Geometrinen elementti Lisäparametrit
Identiteetti Ei vaadita Ei mitään
Käännös Ei vaadita Vektori $\mathbf{t}$
Heijastus tasossa A Tasossa A Ei ole
Liukuheijastus =heijastus tasossa A ja käännös. $\mathbf{v}$ yhdensuuntainen A:n kanssa Taso A Liukuvektori $\mathbf{v}$
Kierto viivan b ympäri viiva b viiva b Kulma ja pyörimissuunta
Ruuvin kierto = kierto viivan b ympäri ja translaatio $\mathbf{u}$ b:n suuntainen Viiva b Kulma ja pyörimissuunta ruuvivektorin $\\mathbf{u}$
Rotoinversio = kierto suoran b ympäri ja inversio pisteen P kautta b:llä Line b ja piste P pisteessä b Kulma (ei yhtä suuri kuin $\pi$) ja kiertosuunta
Inversio pisteen P kautta Pisteen P kautta Pisteen P kautta Ei mitään

Vuoden 1989 raportissa lueteltua symbolia Eg voidaan käyttää liukutasoille, jos halutaan vain osoittaa, että symmetriaelementti on liukutaso. Toisaalta, jos se kuuluu johonkin niistä erityislajeista, joita on jo pitkään merkitty sopivalla kirjaimella (a, b, c, n tai d; vrt. ITA83), kyseinen kirjain korvaa Eg:ssä olevan g:n.

Taulukko 2. Symmetriaelementit piste- ja avaruusryhmissä
Symmetriaelementin nimi Symboli Geometrinen elementti Määritysoperaatio (d.o.) Operaatiot elementtijoukossa
Peilitaso Em Taso A Heijastus A:ssa D.o. ja sen koplanaariset vastineet*
Leikkaustaso Eg\ddag Taso A Leikkausheijastus A:ssa, 2v (ei v) ristikkokäännös D.o. ja sen koplanaariset vastineet*
Kiertoakseli En Linja b Kierto b:n ympäri, kulma $2\pi/n$ ,n = 2, 3, 4 tai 6 1.,$\pisteiden$,(n – 1)-l. potensseja d.o:n. ja niiden koaksiaaliset vastineet\dag
Ruuvin akseli Enj Linja b Ruuvin kierto b:n ympäri, kulma $2\pi/n$, u =j/n kertaa lyhimmän ristikon
käännös b:tä pitkin, oikean ruuvin; n = 2, 3, 4 tai 6, $j=1,\dots,(n-1)$ 		1st,$\dots$,(n – 1)th d:n potenssit.o. ja niiden koaksiaaliset vastineet\dag
Rotoinversioakseli $E\bar n$ Viiva b ja piste P b:llä Rotoinversio: kierto b:n ympäri, kulma $2\pi/n$ ja inversio P:n kautta; n = 3, 4 tai 6 D.o. ja sen inversio
Keskipiste $E\bar 1$ Piste P Inversio P:n kautta D.o. vain

* Eli kaikki liukuheijastukset, joilla on sama heijastustaso ja joiden liukuheijastusvektorit eroavat d.o.:n vektoreista (jotka otetaan nollaksi heijastuksen osalta) ristikon translaatiovektorilla.
\dag Se tarkoittaa kaikkia kiertoja ja ruuvikiertoja, joilla on sama akseli b, sama kiertokulma ja -suunta ja sama ruuvivektori$\mathbf{u}$(nolla kiertoa varten) ristikkokäänteisvektorin verran.
\ddag Eg:ssä g korvataan a:lla, b:llä, c:llä, n:llä, d:llä, e:llä tai k:lla tietynlaisten liukutasojen kohdalla, vrt. 2 §.

Eb:n kaltaisten symbolien tärkeään uuteen puoleen voidaan kuitenkin viitata. ITA83:n mukaan tason merkitseminen b:llä tarkoitti vain sitä, että tasossa tapahtuva liukuheijastus, jonka liukukomponentti b/2 on b-akselin suuntainen, on symmetriaoperaatio. Tämä määritelmä pätee varmasti kuvassa 1 esitettyyn tilanteeseen.

Fig. 1. (W. Fischerin mukaan.) Eb-liukutason elementtijoukko, joka on esitetty tason yläpuolella (+) ja alapuolella (-) olevien pisteiden joukkona, jotka syntyvät tasossa olevien liukuheijastusten tuloksena, alkaen esimerkiksi vasemmassa yläkulmassa olevasta +-merkistä. Tason suuntaisten translaatioiden (+$\cdots$ + vektorit) netto N on merkitty verkolla, joka tässä tapauksessa sattuu olemaan suorakulmainen. Molemmat reunaparit ovat kristalliakselien suuntaisia. On olemassa liukuheijastus, jonka liukuvektori (+ $\cdots$ -) on b-akselin suuntainen.

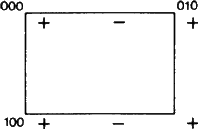
\begin{figure} \includegraphics {fig1.ps} \end{figure}

Kuva 1, samoin kuin kuvat 2 ja 3, on mukailtu Ad-hoc-komitean jäsenen W. Fischerin suunnittelemasta samankaltaisten kuvien sarjasta, joka on tarkoitettu kaikkien liukukalustotyyppien luetteloksi. Vaikka sarja esiteltiin komitealle vuonna 1980, kauan ennen kuin vuoden 1989 raportti ilmestyi, kukin sen kuvista osoittaa täsmälleen liukukoneen ”elementtisarjan” sellaisena kuin se on määritelty kyseisessä raportissa (ks. edellä oleva yhteenveto). Liukutason osalta elementtijoukko koostuu kaikista liukutason heijastuksista, joiden yhteinen geometrinen elementti on taso. Niiden toiminta esitetään projisoituna tähän tasoon. Minkä tahansa +-merkin lähtökohdasta jokainen -merkki on seurausta yhdestä joukon liukuheijastuksista. Kaikki nämä esitetään +- ja -merkkien muodostaman kaksiulotteisen jaksollisen kuvion alkeisverkossa.

Viittaamme usein kaikkien tason suuntaisten käännösten muodostamaan verkkoon N; tämä verkko on helppo havainnollistaa tarkastelemalla vain +-merkkejä. Nämä vektorit on erotettava jyrkästi vektoreista, jotka yhdistävät +-merkin mihin tahansa -merkkiin, joista kukin on elementtijoukkoon kuuluvan liukuhajonnan liukuvektori.

Uusi näkökohta syntyy siitä, että joissakin tapauksissa b-liukutason määritelmän ITA83 mukaan b-liukutaso on myös a-liukutaso; ks. kuva 2. Selkeästi näin tapahtuu vain, jos verkko N on ortogonaalisesti keskitetty, koska silloin a-liukutaso voidaan muuttaa b-liukutasoksi (ja päinvastoin) lisäämällä keskityskäännös. Tähänastinen käytäntö on ollut kutsua tällaista liukutasoa mielivaltaisesti joko a:ksi tai b:ksi, mikä aiheuttaa perusteettoman vääristymän ja näiden symbolien yksikäsitteisyyden puutteen. Tämän vuoksi ehdotamme, että kuvan 2 tapaukselle annetaan erillinen symboli.

Fig. 2. (W. Fischerin mukaan.) Ee-liukutason alkiojoukko. Vrt. kuvan 1 kuvateksti. Huomaa, että verkko N on tässä ortogonaalisesti keskitetty.

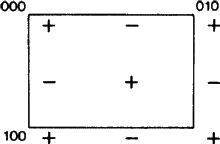
\begin{figure} \includegraphics {fig2.ps} \end{figure}

Tällöin tämän symbolin soveltamisalaa olisi laajennettava koskemaan liukutasoja, jotka ovat diagonaalisuuntaisia eli yhden kideakselin suuntaisia, edellyttäen, että liukutasolla on liukuvektori tuon akselin suuntainen ja että verkko N on ortogonaalisesti keskitetty. Tällaisten tasojen osalta ei ole edellä esitetyn a-b-sattumanvaraisen valinnan epäselvyyttä, vaan uuden symbolin laajennettu soveltamisala vastaa kaikkien nykyisten symbolien (eli a, b, c, n ja d) soveltamisalaa. Kutakin näistä käytetään liukutasolle, jossa on sekä yksi että kaksi kideakselia verkossa N, vrt. kuva 3.

Uudeksi symboliksi ehdotetaan kirjainta e. Näin ollen Ee koskee liukutasoja, joissa on ortogonaaliset keskitetyt verkot N ja vähintään yksi liukuvektori kideakselin varrella. Tarvitaan siis uusi kriteeri: nimittäin liukuvektoreiden suuntaus suhteessa kiteen tavanomaisiin akseleihin. Koska jälkimmäiset ovat symmetrisuuntia pitkin, kun taas jokainen liukuvektori on yhdensuuntainen ristikon peilitason kanssa, ei ole yllättävää, että N:ssä on aina vähintään yksi kiteen tavanomainen akseli. Jos tällaisia akseleita on vain yksi, N:ssä on aina toinenkin siirtymä kohtisuorassa sitä vastaan.

Uusi symboli e sekä vanhat symbolit a, b, c, d, n määritellään nyt uudelleen tämän uuden kriteerin ja Bravais’n verkkotyypin N suhteen. Tämä verkko on monokliininen tai ortogonaalinen tai tetragonaalinen primitiivinen (mp tai op tai tp) tai ortogonaalisesti keskitetty (oc). Vain oc-tyyppiset verkot N sallivat Ee-liukutason. Symboli En soveltuu Bravais-tyypin mp- tai op-verkoille N, kun taas Ed soveltuu oc-tyypin verkoille N. (Kuten ITA83:n taulukon 1.3 alaviitteessä todetaan: ”Liukutasoja d esiintyy vain orthorhombisissa F-avaruusryhmissä, tetragonaalisissa I-avaruusryhmissä ja kuutiollisissa I- ja F-avaruusryhmissä. Ne esiintyvät aina pareittain vuorottelevien liukuvektoreiden kanssa”). Toisin kuin Ea-, Eb-, Ec- ja Ee-tasojen kohdalla, En- ja Ed-tasojen kohdalla ei kuitenkaan ole yhtään liukuvektoria, joka olisi yhdensuuntainen tai kohtisuorassa N:ssä olevan tavanomaisen akselin kanssa.

Yllämainittujen liukutasojen määritelmät on esitetty tiivistetysti taulukon 3 riveillä (i) ja (ii) sekä selvemmin kuvassa 3.

Taulukko 3. Taulukon 3. Painetut symbolit erityyppisille liukutasoille

Symboli määräytyy kahden kriteerin perusteella. Toinen kriteeri on tarkasteltavan tason suuntaisten symmetriakäänteiden muodostaman verkon N Bravais-tyyppi (mp, op, tp tai oc). Tämä verkko sisältää aina vähintään yhden tavanomaisen kideakselin.* Toinen kriteeri viittaa liukuvektoreiden suuntautumiseen tällaisiin akseleihin nähden.
Kideakseleihin nähden samansuuntaisten tai kohtisuorassa olevien liukuvektoreiden lukumäärä verkossa N Bravais-tyyppinen verkko N
m, op, tp oc
(i) Yksi tai kaksi yhdensuuntaista Ec(Ea, Eb) Ee
(ii) Ei yhtään rinnakkaista, ei yhtään kohtisuoraa En Ed
(iii) Ei yhtään rinnakkaista, yksi kohtisuoraa Ek –

* Määriteltynä ITA83:n 9 §:n mukaisesti.1; rhomboedristen avaruusryhmien osalta käytetään tässä kuitenkin vain heksagonaalisia akseleita.

Kaikki loput liukulentokoneet olivat aiemmin ilman erityistä tunnusta. Niillä kaikilla on diagonaalinen orientaatio (vain yksi tavanomainen kideakseli netto N:ssä). Niiden elementtijoukon liukuheijastuksista yhdelläkään ei ole liukuvektoria kyseistä akselia pitkin. Yksi liukuvektori on kuitenkin (symmetrian vuoksi) kohtisuorassa sitä vastaan. Symboli vaikuttaa toivottavalta, joten ehdotetaan jälleen uutta kirjainta: k. Uusi symboli Ek määritellään lyhyesti taulukon 3 rivillä (iii), ja sitä havainnollistetaan täysin kuvan 3 alemmassa lohkossa. Joitakin esimerkkejä annetaan 2 §:ssä.

Fig. 3. (Mukautettu W. Fisherin piirustuksista.) Liukutasojen elementtisarjojen kaikki mahdolliset näkökohdat esitetty kuten kuvassa 1, mutta akselimerkinnöistä riippumatta. Kaaviot on ryhmitelty sarakkeisiin, joiden otsikkona on niiden verkkojen N Bravais-verkkotyyppinen symboli (yläviiva), vrt. taulukko 3. Taulukon muut kriteerit tarkistetaan tarkastelemalla ensin kaksoisviivoja, jotka osoittavat kideakselien suunnat tasossa. Näytetyn N-verkon yksi reuna (pystysuora) valitaan aina tällaisen akselin suuntaiseksi. Toinen reuna on vaakasuora lukuun ottamatta kohtia (1) ja (8). Kaavioissa (1),$\dots$,(5) liukutason symboli on pystysuoran akselin merkintä a, b tai c; muissa kaavioissa se on kaavion sisältävän hahmotellun lohkon ympyröity kirjain. Huomaa pystysuorat liukuvektorit kaavioissa (1),$\dots$,(7), vaakasuorat vektorit kaavioissa (6), (7), (14), (15) ja kummankaan puuttuminen kaavioista (8),$\dots$,(13). Kunkin kaavion alla on esimerkki esiintymisestä avaruusryhmän symbolin ja tason koordinaattikolmikon avulla.

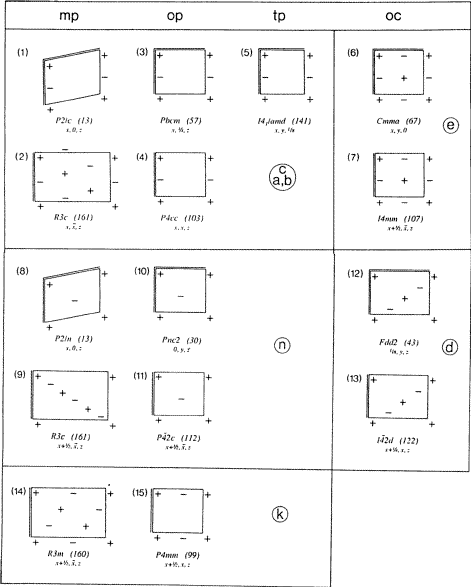
\begin{figure} \includegraphics {fig3.ps} \end{figure}

Kuvassa 3 on esitetty Fischerin inventaario kaikista liukutasotyypeistä lyhennettynä – vaikkakin edelleen täydellisenä – tavalla, jossa kideakseleille on annettu enemmän graafista painoarvoa. Kunkin kaavion kohdalla on lueteltu yksi esimerkki sen esiintymisestä avaruusryhmässä.

Joissain rhomboedrisissä avaruusryhmissä esiintyy diagonaalisesti suuntautuneita Ec-, En- ja Ek-tasoja mp-tyyppisillä verkoilla N, jotka voidaan kuvata ortogonaalisen verkon kolminkertaisella keskittämisellä. Verkon N suorakulmainen kolminkertainen verkko on esitetty tällaisille liukutasotyypeille kuvassa 3, kaavioissa (2), (9) ja (14). Kaaviossa (9) tunnistetaan samankaltaisuus muihin n-kaavioihin, kuten (8) tai (10), jos (9) tarkastellaan verkon N monokliinistä primitiiviverkkoa, jossa on diagonaaliset liukuvektorit.

Symmetriaelementtien graafiset symbolit

Tässä olevat graafiset symbolit, sellaisina kuin ne on määritetty ja joita käytetään ITA83:ssa, ovat ad hoc -komitean mielestä riittäviä yhtä poikkeusta lukuun ottamatta. Tilanne on hyvin erilainen kuin painettujen symbolien kohdalla, koska piirustuksissa projektiosuunta on lisätty parametri. Jäljempänä käytetyissä termeissä ”kohtisuora projektio” ja ”samansuuntainen projektio” kohtisuora ja samansuuntainen viittaavat projektiosuunnan suuntaukseen liukutason suhteen.

Ee-tasolle on olemassa symboli sen kohtisuoraa projektiota varten. Ee-liukutason yhdensuuntaista projektiota kuvaavat olemassa olevat graafiset symbolit kärsivät kuitenkin samasta epäselvyydestä kuin painetut symbolit. Ne ilmaisevat liukuvektorin joko yhdensuuntaisesti tai kohtisuoraan projektiosuuntaan nähden, mutta valinta on mielivaltainen. Sen vuoksi ehdotetaan uutta symbolia Ee-liukutason yhdensuuntaiselle projektiolle, nimittäin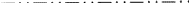

Esimerkkejä Ee-tasoista.

Kaikki kahden akselin suuntaiset liukutasot avaruusryhmissä Fmm2, Fmmm, $Fm\bar 3$, $Fm\bar 3m$ ja $Fm\bar 3c$ (N:o 42, 69, 202, 225 ja 226) sekä tietyt tasot viidessä 3 §:ssä luetellussa avaruusryhmässä.

Diagonaalisesti suuntautuneita Ee-tasoja esiintyy avaruusryhmissä I4mm, I4cm, $I\bar 42m$, I4/mmm, I4/mcm, $I\bar 43m$ ja $Im\bar 3m$ (Nro. 107, 108, 121, 139, 140, 217 ja 229).

ITA83:ssa kaikki nämä Ee-tasot on piirretty melko mielivaltaisesti joko katkoviivoin tai katkoviivoin niiden rinnakkaisprojektioihin. Kuvassa 4 on esitetty avaruusryhmän I4cm (nro 108) kaavio sekä ITA83:ssa esitetyllä tavalla että uutta symbolia käyttäen.

Kuva 4. Avaruusryhmän I4cm (nro 108) kaavio. (a) ITA83:sta otettu avaruusryhmän I4cm (nro 108) kaavio. (b) Sama, muokattuna käyttämällä 2 §:ssä ehdotettua graafista symbolia Ee-tason rinnakkaisprojektiota varten.

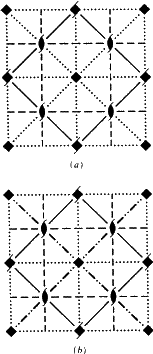
\begin{figure} \includegraphics {fig4.ps} \end{figure}

Vaikka Ek on uusi tulostussymboli, ITA83:n kaavioissa kaikki liukutasot Ek on piirretty tyydyttävästi samoilla konventioilla kuin Ea/b/c-liukutasot. Kuten näissäkin tapauksissa, on olemassa yksi erityinen liukuvektori (kohtisuorassa kideakseliin nähden verkossa N, vrt. taulukko 3). Kun tämä vektori on esimerkiksi yhdensuuntainen projisointitason kanssa, Ek-taso piirretään aina kyseisen yleissopimuksen mukaisena katkoviivana. Siksi Ek-liukutasoille ei ehdoteta uutta graafista symbolia.

Esimerkkejä Ek-tasoista.

Tällaiset tasot löytyvät helposti ITA83:n kaavioista vain yhden akselin suuntaisina tasoina, jotka on projisoitu katkoviivoina, esim. xxz P4bm:ssä ja $P\bar 42_1m$ (N:o 100 ja 113). Erityisesti taulukko 3 on täsmälleen sopusoinnussa Ek- ja En-tasojen välisen eron kanssa. Ks. esimerkiksi R3m:n ja R3c:n katkoviivat ja pistekatkoviivat (nro 160 ja 161).

Hermann-Mauguinin avaruusryhmän symbolit

Avaruusryhmän Hermann-Mauguinin (HM) symbolin ristikkokirjaimen jälkeen esiintyvät merkit oli alunperin tarkoitettu kuvaamaan ryhmän generointioperaatioita. Esimerkiksi b oli b-liukuheijastus tasossa, joka oli suunnattu HM-symbolissa olevan sijaintinsa mukaisesti.

Käytännössä operaatioiden tilalle tulivat suositut, joskin huonosti määritellyt symmetriaelementit. Niinpä b alettiin nähdä liukutasona, Eb:nä nykyisessä terminologiassamme. Tästä uudelleentulkinnasta ei ole mitään haittaa paitsi silloin, kun operaatio kuuluu Ee-liukutasoon. Jos tämä pätee esimerkiksi edellä mainittuun b-liukutason heijastukseen, on olemassa Ee-liukutaso mutta ei Eb-liukutasoa vastaavassa orientaatiossa. Tällöin b:stä tulee hyvin harhaanjohtava merkki. Tämän lisäksi harhaanjohtavuus (joka annetaan b:lle a:n tai c:n sijaan) on aivan yhtä häiritsevä kuin §1:ssä käsiteltyjen symmetriaelementtisymbolien tapauksessa.

Sentähden ehdotetaan, että tällaiset harhaanjohtavat kirjaimet a tai b korvataan e:llä kaikissa viidessä HM-symbolissa, joissa ne esiintyvät:

Avaruusryhmä No. 39 41 64 67 68
Symboli ITA83:ssa: Abm2 Aba2 Cmca Cmma Ccca
Uusi symboli: Aem2 Aea2 Cmce Cmme Ccce.

Ehdotettujen uusien symbolien etuna on myös se, että e – toisin kuin a tai b – on neutraali eikä siten muutu akselipermutaation yhteydessä.

Symmetriaoperaatioiden tulostetut symbolit

Täydellisen tulostettujen symbolien sarjan on suunnitellut W. Fischer & E. Koch (ITA83, §11.2) ja sitä sovellettiin laajasti avaruusryhmäkuvausten symmetriaoperaatioita koskevissa osioissa.

Lyhyesti sanottuna jokainen symboli koostuu enintään kolmesta osasta. Ensimmäinen osa on yksittäinen merkki (joskus indeksin kanssa), joka kuvaa operaation lajia. Seuraava osa (seuraavat osat) antaa (antavat) asiaankuuluvan siirto- tai translaatiovektorin komponentit – aina suluissa – ja operaation geometrisen elementin koordinaatit tässä järjestyksessä.

Tätä järjestelmää harkittuaan tilapäiskomitea haluaa ottaa käyttöön kaksi muutosta liukupeilojen osalta:

(i) nykyisen ensimmäisen merkin (joka voi olla a, b, c, n, d tai g) sijasta kirjoitetaan aina kirjain g;

(ii) liukuvektorin komponentit (suluissa) kirjoitetaan aina kokonaisuudessaan, erityisesti yksinkertaisten liukupeilojen kohdalla a-, b- tai c- liukupeilojen osalta silloin, kun ne on aiemmin jätetty pois.

Sääntö (i) jättää pois tiedon siitä, millaiseen liukutasoon operaatio kuuluu. Hyvin usein tämä tieto on epäolennaista tai jopa hämmentävää. A/b/c-tasojen osalta tukahduttaminen voi tuhota olennaisen informaation, mutta menetys korjataan säännöllä (ii), kuten alla olevassa esimerkissä on esitetty.

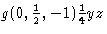Tämän muutoksen avulla symbolien yhdenmukaisuus – myös kiertoja koskevien symbolien osalta – paranee huomattavasti. Esimerkiksi tasossa $x = \frac{1}{4}$ tapahtuvan liukuheijastuksen symboli, jossa on epätavallinen liukuvektori $(0, \frac{1}{2}, -1)$<, nimittäin $g(0, \frac{1}{2}, 1) \frac{1}{4}yz$<, vastaa nyt yksinkertaisen b-liuskaheijastuksen symbolia. ITA83:ssa jälkimmäistä merkittiin $b \frac{1}{4} y z$ , mutta tämä muuttuu säännön (ii) avulla $g(0, \frac{1}{2}, 0) \frac{1}{4} y z$.

Ylläolevat säännöt pätevät yhtä lailla peilitason alkiojoukkoon kuuluviin liukuheijastuksiin. Jos siis tällaisen operaation siirtokomponentti on (0, 1, 2), niin sen symboli alkaa g(0, 1, 2), ei m(0, 1,2).

International Tables for Crystallography (1983). Vol. A, toimittanut TH. HAHN, erityisesti §§ 1.1, 1.3, 1.4, 7 ja 11. Dordrecht: Kluwer Academic Publishers.

International Tables for Crystallography (1989). Vol. A, 2., uudistettu, ed., toimittanut TH. HAHN. Dordrecht: Kluwer Academic Publishers.

WOLFF, P. M. DE, BELOV, N. V., BERTAUT, E. F., BUERGER, M. J., DONNAY, J. D. H., FISCHER, W., HAHN, TH., KOPTSIK, V. A., MACKAY, A. L., WONDRATSCHEK, H., WILSON, A. J. C. & ABRAHAMS, S. C. (1985). Acta Cryst. A41, 278-280.

WOLFF, P. M. DE, BILLIET, Y., DONNAY, J. D. H., FISCHER, W., GALIULIN, R. B., GLAZER, A. M., SENECHAL, M., SHOEMAKER, D. P., WONDRATSCHEK, H., HAHN, TH., WILSON, A. J. C. & ABRAHAMS, S. C. (1989). Acta Cryst. A45, 494-499.

…vektorit. Kuvan 3 kolmen kaavion (2), (9) ja (14) liukutason symbolit c, n ja k on luonnollisesti annettu taulukon 3 mukaisesti. Eräs tilapäisen komitean jäsen (professori Wondratschek) on sitä mieltä, että symboli n kaaviossa (9) on ristiriidassa perinteisten käsitysten kanssa n-tasoista. Hän ehdottaa, että kuviolle (9) annetaan erityinen symboli. Tämä ehdotus ei kuitenkaan ole saanut riittävästi kannatusta tilapäiskomiteassa.

Vastaa

Sähköpostiosoitettasi ei julkaista.