În timp ce metodele din secțiunea precedentă sunt utile pentru a descrie și afișa date din eșantioane, adevărata putere a statisticii se dezvăluie atunci când folosim eșantioane pentru a ne oferi informații despre populații. În acest context, o populație este întreaga colecție de obiecte de interes, de exemplu, prețurile de vânzare pentru toate casele unifamiliale de pe piața imobiliară reprezentată de setul nostru de date. Am dori să știm mai multe despre această populație pentru a ne ajuta să luăm o decizie cu privire la ce locuință să cumpărăm, dar singurele date pe care le avem sunt un eșantion aleatoriu de 30 de prețuri de vânzare.

Cu toate acestea, putem folosi „gândirea statistică” pentru a face deducții despre populația de interes prin analiza datelor eșantionului. În special, folosim noțiunea de model – o abstractizare matematică a lumii reale – pe care îl potrivim la datele eșantionului. Dacă acest model oferă o potrivire rezonabilă a datelor, adică dacă poate aproxima modul în care variază datele, atunci presupunem că poate aproxima și comportamentul populației. Modelul oferă apoi baza pentru luarea de decizii cu privire la populație, de exemplu, prin identificarea modelelor, explicarea variației și prezicerea valorilor viitoare. Desigur, acest proces poate funcționa numai dacă datele eșantionului pot fi considerate reprezentative pentru populație.

Câteodată, chiar și atunci când știm că un eșantion nu a fost selectat în mod aleatoriu, putem totuși să îl modelăm. Atunci, s-ar putea să nu putem să deducem în mod formal despre o populație din eșantion, dar putem totuși să modelăm structura de bază a eșantionului. Un exemplu ar fi un eșantion de conveniență – un eșantion selectat mai mult din motive de conveniență decât pentru proprietățile sale statistice. Atunci când se modelează astfel de eșantioane, orice rezultate trebuie raportate cu avertismentul de a restricționa orice concluzii la obiecte similare celor din eșantion. Un alt tip de exemplu este cel în care eșantionul cuprinde întreaga populație. De exemplu, am putea modela datele pentru toate cele 50 de state ale Statelor Unite ale Americii pentru a înțelege mai bine orice tipare sau asociații sistematice între state.

Din moment ce lumea reală poate fi extrem de complicată (în modul în care valorile datelor variază sau interacționează împreună), modelele sunt utile deoarece simplifică problemele astfel încât să le putem înțelege mai bine (și apoi să luăm decizii mai eficiente). Prin urmare, pe de o parte, avem nevoie ca modelele să fie suficient de simple pentru a le putea folosi cu ușurință pentru a lua decizii, dar, pe de altă parte, avem nevoie de modele care să fie suficient de flexibile pentru a oferi aproximări bune la situații complexe. Din fericire, de-a lungul anilor au fost dezvoltate multe modele statistice care oferă un echilibru eficient între aceste două criterii. Un astfel de model, care oferă un bun punct de plecare pentru modelele mai complicate pe care le vom lua în considerare mai târziu, este distribuția normală.

Din punct de vedere statistic, o distribuție de probabilitate este un model teoretic care descrie modul în care variază o variabilă aleatoare. În scopurile noastre, o variabilă aleatoare reprezintă valorile datelor de interes din populație, de exemplu, prețurile de vânzare ale tuturor locuințelor unifamiliale de pe piața noastră imobiliară. Un mod de a reprezenta distribuția populațională a valorilor datelor este o histogramă, așa cum este descrisă în secțiunea 1.1. Diferența acum constă în faptul că histograma afișează întreaga populație și nu doar eșantionul. Deoarece populația este mult mai mare decât eșantionul, intervalele (bins) ale histogramei (intervalele consecutive ale datelor care cuprind intervalele orizontale pentru bare) pot fi mult mai mici, de exemplu, în cele ce urmează este prezentată o histogramă pentru o populație simulată de 1.000 de prețuri de vânzare.

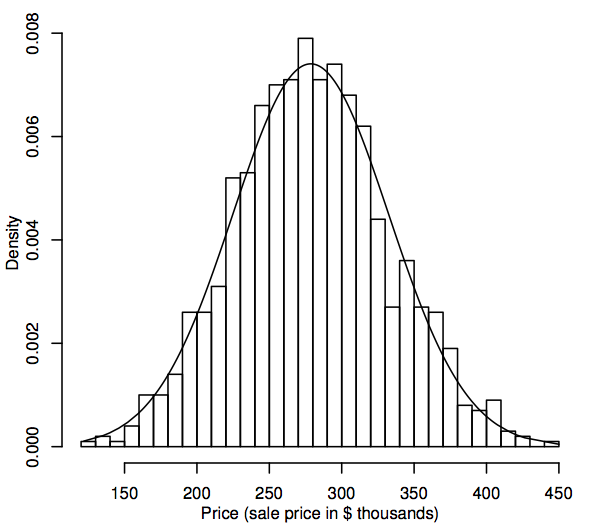
Pe măsură ce dimensiunea populației devine mai mare, ne putem imagina barele histogramei devenind mai subțiri și mai numeroase, până când histograma seamănă mai degrabă cu o curbă netedă decât cu o serie de trepte. Această curbă netedă se numește curbă de densitate și poate fi privită ca fiind versiunea teoretică a histogramei populației. Curbele de densitate oferă, de asemenea, o modalitate de a vizualiza distribuțiile de probabilitate, cum ar fi distribuția normală. O curbă de densitate normală este suprapusă peste histograma de mai sus. Histograma populației simulate urmează curba destul de îndeaproape, ceea ce sugerează că această distribuție a populației simulate este destul de apropiată de cea normală.

Pentru a vedea cum o distribuție teoretică se poate dovedi utilă pentru a face inferențe statistice despre populații, cum ar fi cea din exemplul nostru cu prețurile locuințelor, trebuie să analizăm mai îndeaproape distribuția normală. Pentru început, luăm în considerare o versiune particulară a distribuției normale, normala standard, așa cum este reprezentată de următoarea curbă de densitate.

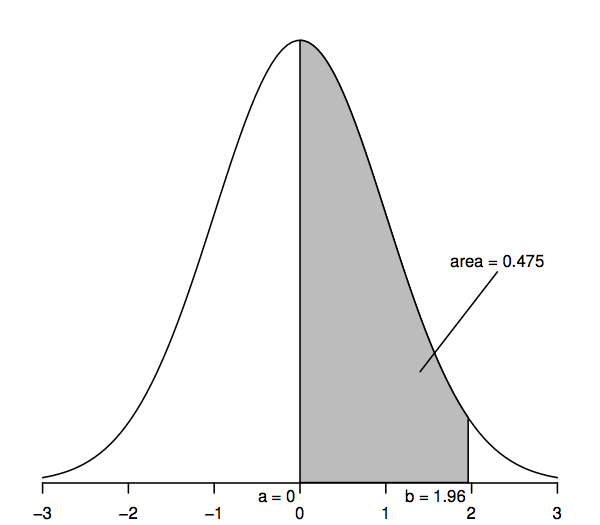
Variabilele aleatoare care urmează o distribuție normală standard au o medie de 0 (astfel încât curba este simetrică în jurul valorii 0, care se află sub punctul cel mai înalt al curbei) și o abatere standard de 1 (astfel încât curba are un punct de inflexiune – unde curba se îndoaie mai întâi într-o direcție și apoi în cealaltă – la +1 și -1). Curba densității normale este uneori numită „curba clopotului”, deoarece forma sa seamănă cu cea a unui clopot.

Caracteristica cheie a curbei densității normale care ne permite să facem deducții statistice este că zonele de sub curbă reprezintă probabilități. Întreaga arie de sub curbă este unu, în timp ce aria de sub curbă dintre un punct de pe axa orizontală (a, să zicem) și un alt punct (b, să zicem) reprezintă probabilitatea ca o variabilă aleatoare care urmează o distribuție normală standard să se situeze între a și b. Deci, de exemplu, figura de mai sus arată că probabilitatea este 0.475 ca o variabilă aleatoare normală standard să se situeze între a=0 și b=1,96, deoarece aria de sub curbă între a=0 și b=1,96 este 0,475.

Potem obține valori pentru aceste arii sau probabilități dintr-o varietate de surse: tabele cu numere, calculatoare, programe de calcul sau de statistică, site-uri web și așa mai departe. Mai jos vom tipări doar câteva valori selectate, deoarece majoritatea calculelor ulterioare utilizează o generalizare a distribuției normale numită „distribuție t”. De asemenea, mai degrabă decât zone precum cea umbrită în figura de mai sus, va deveni mai util să se ia în considerare „zonele de coadă” (de ex, la dreapta punctului b), și astfel, pentru coerență cu tabelele numerice ulterioare, tabelul următor permite calcularea unor astfel de arii de coadă:

În special, aria cozii superioare la dreapta lui 1,96 este 0,025; acest lucru este echivalent cu a spune că aria dintre 0 și 1,96 este 0,475 (deoarece întreaga arie de sub curbă este 1, iar aria la dreapta lui 0 este 0,5). În mod similar, aria cu două cozi, care este suma ariilor din dreapta lui 1,96 și din stânga lui -1,96, este de două ori 0,025, sau 0,05.

Cum ne ajută toate acestea să facem inferențe statistice despre populații, cum ar fi cea din exemplul nostru cu prețurile locuințelor? Ideea esențială este că potrivim un model de distribuție normală la datele din eșantionul nostru și apoi folosim acest model pentru a face inferențe despre populația corespunzătoare. De exemplu, putem utiliza calculele de probabilitate pentru o distribuție normală (așa cum se arată în figura de mai sus) pentru a face afirmații de probabilitate despre o populație modelată cu ajutorul acelei distribuții normale – vom arăta exact cum să facem acest lucru în secțiunea 1.3. Înainte de a face acest lucru, însă, facem o pauză pentru a lua în considerare un aspect al acestei secvențe inferențiale care poate face sau nu procesul. Oferă modelul o aproximare suficient de apropiată de tiparul valorilor eșantionului încât să putem fi siguri că modelul reprezintă în mod adecvat valorile populației? Cu cât aproximația este mai bună, cu atât mai fiabile vor fi afirmațiile noastre inferențiale.

Am văzut mai devreme cum o curbă de densitate poate fi considerată ca o histogramă cu o dimensiune foarte mare a eșantionului. Așadar, o modalitate de a evalua dacă populația noastră urmează un model de distribuție normală este de a construi o histogramă din datele eșantionului nostru și de a determina vizual dacă aceasta „pare normală”, adică aproximativ simetrică și în formă de clopot. Aceasta este o decizie oarecum subiectivă, dar, cu experiență, ar trebui să constatați că devine mai ușor să discerneți histogramele clar nenormale de cele care sunt rezonabil de normale. De exemplu, în timp ce histograma de mai sus arată în mod clar ca o curbă de densitate normală, normalitatea histogramei celor 30 de prețuri de vânzare de probă din secțiunea 1.1 este mai puțin sigură. O concluzie rezonabilă în acest caz ar fi că, deși această histogramă de eșantion nu este perfect simetrică și în formă de clopot, ea este suficient de apropiată pentru ca histograma corespunzătoare (ipotetică) a populației să fie foarte bine normală.

O modalitate alternativă de a evalua normalitatea este de a construi un QQ-plot (quantile-quantile plot), cunoscut și sub numele de grafic de probabilitate normală, așa cum se arată aici pentru datele privind prețurile locuințelor:

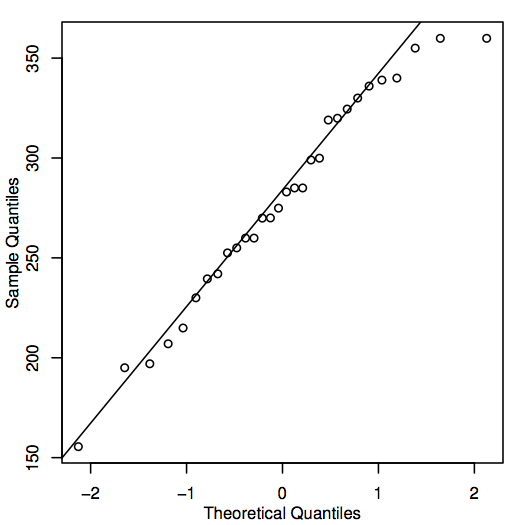
Dacă punctele din QQ-plot se află aproape de linia diagonală, atunci valorile corespunzătoare ale populației ar putea foarte bine să fie normale. Dacă punctele se află în general departe de linie, atunci normalitatea este pusă sub semnul întrebării. Din nou, aceasta este o decizie oarecum subiectivă care devine mai ușor de luat odată cu experiența. În acest caz, având în vedere dimensiunea destul de mică a eșantionului, punctele sunt probabil suficient de aproape de linie încât este rezonabil să se concluzioneze că valorile populației ar putea fi normale.

Există, de asemenea, o varietate de metode cantitative pentru evaluarea normalității – a se vedea secțiunea 6.3.