Definiție
Un polinom în variabila x este o funcție care poate fi scrisă sub forma,
unde an, an-1 , …, a2, a1, a0 sunt constante. Numim termen conducător termenul care conține cea mai mare putere a lui x (adică anxn) și numim an coeficientul conducător. Gradul polinomului este puterea lui x din primul termen. Am văzut deja polinoame de gradul 0, 1 și 2, care reprezentau funcțiile constantă, liniară și, respectiv, pătratică. Polinoamele de gradul 3, 4 și 5 au, de asemenea, denumiri speciale: funcții cubice, cuartice și quintice. Polinoamele cu gradul n > 5 se numesc pur și simplu polinoame de gradul n. Denumirile diferitelor funcții polinomiale sunt rezumate în tabelul de mai jos.
| Degresul polinomului | Numele funcției |
| 0 | Funcție constantă |
| 1 | Funcție liniară |
| 2 | Funcție pătratică |
| 3 | Funcția cubică |
| 4 | Funcția cuartică |
| 5 | Funcția cintică |
| n (unde n > 5) | polinom de gradul n |
Câteva exemple de polinoame includ:
Comportamentul limită al polinoamelor
Comportamentul limită al unei funcții descrie ceea ce se întâmplă cu funcția pe măsură ce x → ±∞. Gradul unui polinom și semnul coeficientului său principal dictează comportamentul său limită. În particular,
Aceste rezultate sunt rezumate în tabelul de mai jos.
Puteți folosi aceste informații pentru a determina dacă un polinom are sau nu grad par sau impar și dacă coeficientul principal este pozitiv sau negativ, pur și simplu prin inspectarea graficului său.
Următoarele grafice de polinoame exemplifică fiecare dintre comportamentele prezentate în tabelul de mai sus.
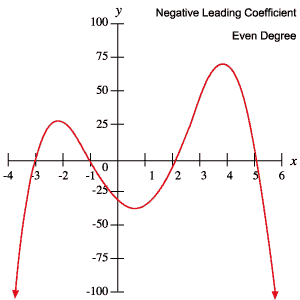
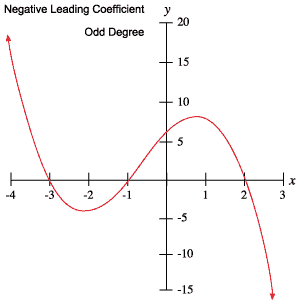
Rădăcini și puncte de răscruce
Gradul unui polinom vă spune chiar mai multe despre el decât comportamentul limită. Mai exact, un polinom de gradul n poate avea cel mult n rădăcini reale (x-intercepte sau zerouri) numărând multiplicitățile. De exemplu, să presupunem că avem în vedere un polinom de gradul 6 care are 4 rădăcini distincte. Dacă două dintre cele patru rădăcini au multiplicitatea 2, iar celelalte 2 au multiplicitatea 1, știm că nu există alte rădăcini, deoarece am luat în calcul toate cele 6 rădăcini. Acest lucru se datorează faptului că rădăcinile cu multiplicitatea 2 (cunoscute și sub numele de rădăcini duble) sunt numărate ca două rădăcini.
Să știți că un polinom de gradul n nu trebuie neapărat să aibă n rădăcini reale – ar putea avea mai puține, deoarece are rădăcini imaginare. Observați că un polinom de grad impar trebuie să aibă cel puțin o rădăcină reală, deoarece funcția se apropie de – ∞ la un capăt și de + ∞ la celălalt; o funcție continuă care trece de la negativ la pozitiv trebuie să intersecteze axa x- undeva la mijloc. În plus, un polinom de gradul n poate avea cel mult n – 1 puncte de cotitură. Un punct de cotitură este un punct în care funcția trece de la creștere la descreștere sau de la descreștere la creștere, așa cum se vede în figura de mai jos. Din nou, un polinom de gradul n-lea nu trebuie să aibă neapărat n – 1 puncte de cotitură, ci poate avea mai puține.
Nota de precauție
Este important să realizăm diferența dintre funcțiile pare și impare și polinoamele de grad par și impar. Orice funcție, f(x), este fie pară dacă,
f(-x) = x,
pentru toate x din domeniul lui f(x), fie impară dacă,
f(-x) = -x,
pentru toate x din domeniul lui f(x), fie nici pară, nici impară dacă niciuna dintre afirmațiile de mai sus nu este adevărată.
Un polinom de gradul k, p(x), se spune că are grad par dacă k este un număr par și grad impar dacă k este un număr impar. Rețineți că, chiar dacă p(x) are grad par, nu este neapărat o funcție pară. De asemenea, dacă p(x) are grad impar, nu este neapărat o funcție impară.
De asemenea, folosim termenii par și impar pentru a descrie rădăcinile polinoamelor. Mai precis, un polinom p(x) are rădăcina x = a de multiplicitate k (adică x = a este o rădăcină repetată de k ori) dacă (x – a)k este un factor al lui p(x). Se spune că x = a are multiplicitate pară dacă k este un număr par și multiplicitate impară dacă k este un număr impar.
Domeniu și domeniu
Toate polinoamele au același domeniu care este format din toate numerele reale. Intervalul polinoamelor de grad impar constă, de asemenea, din toate numerele reale. Domeniul polinoamelor de grad par este un pic mai complicat și nu putem preciza în mod explicit domeniul tuturor polinoamelor de grad par. Dacă coeficientul principal este pozitiv, funcția se va extinde până la + ∞; în timp ce dacă coeficientul principal este negativ, aceasta se va extinde până la – ∞. Aceasta înseamnă că polinoamele de grad par cu coeficientul principal pozitiv au un interval în care ymax reprezintă maximul global pe care îl atinge funcția. În general, nu este posibil să se determine analitic maximele sau minimele polinoamelor.
*****
În secțiunea următoare veți învăța diviziunea polinomială, o tehnică utilizată pentru a găsi rădăcinile funcțiilor polinomiale.
Diviziune polinomială
.