Explicație ilustrată a efectuării convoluțiilor 2D folosind înmulțiri de matrice

În acest articol, voi explica cum sunt implementate convoluțiile 2D ca înmulțiri de matrice. Această explicație se bazează pe notele de la cursul CS231n Rețele neuronale convoluționale pentru recunoaștere vizuală (modulul 2). Presupun că cititorul este familiarizat cu conceptul de operație de convoluție în contextul unei rețele neuronale profunde. Dacă nu, acest repo are un raport și animații excelente care explică ce sunt convoluțiile. Codul pentru a reproduce calculele din acest articol poate fi descărcat de aici.

Small Example

Supunem că avem o imagine 4 x 4 cu un singur canal, X, iar valorile pixelilor săi sunt următoarele:

Supunem, de asemenea, că definim o convoluție 2D cu următoarele proprietăți:

Proprietăți ale operației de convoluție 2D pe care dorim să o efectuăm asupra imaginii noastre

Aceasta înseamnă că vor exista 9 patch-uri de imagine 2 x 2 care vor fi înmulțite element cu element cu matricea W, astfel:

Toate petele de imagine 2 x 2 posibile în X, având în vedere parametrii convoluției 2D. Fiecare culoare reprezintă o parcelă unică

Aceste parcele de imagine pot fi reprezentate ca vectori coloană 4-dimensionali și concatenate pentru a forma o singură matrice 4 x 9, P, astfel:

Observați că a i-a coloană a matricei P este de fapt al i-lea patch de imagine în formă de vector coloană.

Matricea de ponderi pentru stratul de convoluție, W, poate fi aplatizată la un vector de rânduri 4-dimensional , K, astfel:

W ca vector de rânduri aplatizat K

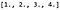
Pentru a efectua convoluția, mai întâi înmulțim matricea K cu P pentru a obține un vector de rânduri 9-dimensional (matrice 1 x 9) care ne dă:

Rezultatul lui K P

Apoi remodelăm rezultatul lui K P la forma corectă, care este o matrice 3 x 3 x 1 (dimensiunea canalului din urmă). Dimensiunea canalului este 1 deoarece am setat filtrele de ieșire la 1. Înălțimea și lățimea este 3 deoarece conform notelor CS231n:

Formula de calcul al înălțimii după aplicarea unei operații de convoluție la o imagine. Formula de calcul al lățimii este aceeași (trebuie doar să înlocuiți înălțimea imaginii și înălțimea nucleului cu lățimea imaginii și, respectiv, lățimea nucleului

Aceasta înseamnă că rezultatul convoluției este:

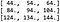
Rezultatul final al efectuării convoluției folosind înmulțiri de matrice

Ceea ce se verifică dacă efectuăm convoluția folosind funcțiile încorporate în PyTorch (a se vedea codul care însoțește acest articol pentru detalii).

Exemplu mai mare

Exemplul din secțiunea anterioară presupune o singură imagine, iar canalele de ieșire ale convoluției sunt 1. Ce s-ar schimba dacă am relaxa aceste ipoteze?

Să presupunem că intrarea noastră în convoluție este o imagine 4 x 4 cu 3 canale cu următoarele valori ale pixelilor:

Valorile pixelilor din imaginea noastră de intrare 4 x 4 x 3

În ceea ce privește convoluția noastră, o vom seta să aibă aceleași proprietăți ca în secțiunea anterioară, cu excepția faptului că filtrele sale de ieșire sunt 2. Aceasta înseamnă că matricea de ponderi inițială, W, trebuie să aibă forma (2, 2, 2, 2, 3), adică (filtrele de ieșire, înălțimea nucleului, lățimea nucleului, canalele imaginii de intrare). Să setăm W pentru a avea următoarele valori:

Valori pentru W având în vedere un kernel 2 x 2, 2 filtre de ieșire și o imagine de intrare cu 3 canale

Observați că fiecare filtru de ieșire va avea propriul nucleu (motiv pentru care avem 2 nuclee în acest exemplu) și canalul fiecărui nucleu este 3 (deoarece imaginea de intrare are 3 canale).

Din moment ce tot convolăm un kernel 2 x 2 pe o imagine 4 x 4 cu 0 zero-padding și stride 1, numărul de patch-uri de imagine este tot 9. Cu toate acestea, matricea de patch-uri de imagine, P, va fi diferită. Mai precis, a i-a coloană a lui P va fi concatenarea valorilor canalelor 1, 2 și 3 (ca vector de coloană) care corespund petei de imagine i. P va fi acum o matrice de 12 x 9. Rândurile sunt 12 deoarece fiecare patch de imagine are 3 canale și fiecare canal are 4 elemente deoarece am stabilit dimensiunea kernelului la 2 x 2. Iată cum arată P:

Matricea de 12 x 9 a petelor de imagine, P

Ca și în cazul lui W, fiecare nucleu va fi aplatizat într-un vector de rânduri și concatenat pe rânduri pentru a forma o matrice de 2 x 12, K. Al i-lea rând din K este concatenarea valorilor canalelor 1, 2 și 3 (sub formă de vector de rând) corespunzătoare celui de-al i-lea nucleu. Iată cum va arăta K:

Matricea de 2 x 12 a valorilor de kernel aplatizate în W, K

Acum, tot ce mai rămâne de făcut este să efectuăm înmulțirea matricei K P și să o redimensionăm la forma corectă. Forma corectă este o matrice 3 x 3 x 3 x 2 (dimensiunea canalului este ultima). Iată rezultatul înmulțirii:

Rezultatul lui K P, o matrice 2 x 9

Și iată rezultatul după remodelarea la o matrice 3 x 3 x 3 x 2:

Ceea ce se verifică din nou dacă pentru a efectua convoluția folosim funcțiile încorporate în PyTorch (vezi codul care însoțește acest articol pentru detalii).

Și ce dacă?

De ce ar trebui să ne intereseze exprimarea convoluțiilor 2D în termeni de înmulțiri de matrice? Pe lângă faptul că dispunem de o implementare eficientă potrivită pentru rularea pe un GPU, cunoașterea acestei abordări ne va permite să raționăm asupra comportamentului unei rețele neuronale convoluționale profunde. De exemplu, He et. al. (2015) au exprimat convoluțiile 2D în termeni de înmulțiri de matrice, ceea ce le-a permis să aplice proprietățile matricelor/vectoarelor aleatoare pentru a argumenta pentru o rutină de inițializare a greutăților mai bună.

Concluzie

În acest articol, am explicat cum să efectuăm convoluții 2D folosind înmulțiri de matrice prin parcurgerea a două exemple mici. Sper că acest lucru este suficient pentru a vă permite să generalizați la dimensiuni arbitrare ale imaginii de intrare și proprietăți de convoluție. Anunțați-mă în comentarii dacă ceva nu este clar.

Convoluție 1D

Metoda descrisă în acest articol se generalizează și la convoluțiile 1D.

De exemplu, să presupunem că intrarea dvs. este un vector 12-dimensional cu 3 canale, astfel:

O intrare care este un vector 12-D cu 3 canale

Dacă setăm convoluția noastră 1D să aibă următorii parametri:

dimensiunea nucleului: 1 x 4
canale de ieșire: 2
stride: 2
padding: 0
bias: 0

Atunci parametrii în operația de convoluție, W, vor fi un tensor cu forma (2 , 3, 1, 4). Să stabilim ca W să aibă următoarele valori:

Valori pentru W. Rețineți că fiecare nucleu este un tensor (3, 1, 4)

În funcție de parametrii operației de convoluție, matricea de patch-uri de „imagine” P, va avea forma (12, 5) (5 patch-uri de imagine unde fiecare patch de imagine este un vector 12-D deoarece un patch are 4 elemente pe 3 canale) și va arăta astfel:

În continuare, aplatizăm W pentru a obține K, care are forma (2, 12) deoarece există 2 nuclee și fiecare nucleu are 12 elemente. Iată cum arată K:

Valorile lui K, o matrice 2 x 12

Acum putem înmulți K cu P care dă:

Rezultatul lui K P, o matrice 2 x 5

În cele din urmă, remodelăm K P la forma corectă, care, conform formulei, este o „imagine” cu forma (1, 5). Aceasta înseamnă că rezultatul acestei convoluții este un tensor cu forma (2, 1, 5), deoarece am setat canalele de ieșire la 2. Iată cum arată rezultatul final: