Posted on

Fază (unde)

, Author

Faza unei oscilații sau a unei unde este fracțiunea unui ciclu complet care corespunde unui decalaj al deplasării față de un punct de referință specificat la momentul t = 0. Faza este un concept din domeniul frecvenței sau al transformării Fourier și, ca atare, poate fi ușor de înțeles în termeni de mișcare armonică simplă. Același concept se aplică mișcării ondulatorii, privită fie la un punct din spațiu pe un interval de timp, fie pe un interval de spațiu la un moment dat. Mișcarea armonică simplă este o deplasare care variază ciclic, așa cum este descrisă mai jos:

File:Mișcarea armonică simplă.png

și descrisă prin formula:

{\displaystyle x(t)=A\cdot \sin(2\pi ft+\theta ),\,}

unde A este amplitudinea oscilației, f este frecvența, t este timpul scurs, iar {\displaystyle \theta } este faza oscilației. Faza determină sau este determinată de deplasarea inițială la momentul t = 0. O mișcare cu frecvența f are perioada {\displaystyle T={\frac {1}{f}}.}

Se pot observa două potențiale ambiguități:

  • Una este că deplasarea inițială a {\displaystyle \cos(2\pi ft+\theta )\,} este diferită de funcția sinusoidală, dar ele par să aibă aceeași „fază”.
  • Unghiul variabil în timp {\displaystyle 2\pi ft+\theta ,\,} sau valoarea sa modulo {\displaystyle 2\pi }, este, de asemenea, denumit în mod obișnuit „fază”. Atunci nu este o condiție inițială, ci mai degrabă o condiție care se schimbă continuu.

Termenul fază instantanee este utilizat pentru a distinge unghiul variabil în timp de condiția inițială. De asemenea, are o definiție formală care este aplicabilă unor funcții mai generale și definește fără ambiguitate faza inițială a unei funcții la t=0. De exemplu, sinusul și cosinusul au în mod inerent faze inițiale diferite. În cazul în care nu se specifică altfel în mod explicit, cosinusul trebuie în general dedus. (vezi și fazor)

Deplasare de fază

File:Phase shift.png

Ilustrație a deplasării de fază. Axa orizontală reprezintă un unghi (fază) care crește cu timpul.

{\displaystyle \theta } este uneori denumită defazaj, deoarece reprezintă o „deplasare” de la faza zero. Dar o schimbare în {\displaystyle \theta } este, de asemenea, menționată ca o deplasare de fază.

Pentru sinusoide infinit de lungi, o schimbare în {\displaystyle \theta } este aceeași cu o deplasare în timp, cum ar fi o întârziere în timp. Dacă {\displaystyle x(t)\,} este întârziată (decalată în timp) cu {\displaystyle {\begin{matrix}{\frac {1}{4}}\end{matrix}}\,} din ciclul său, aceasta devine:

{\displaystyle x(t-{\begin{matrix}{\frac {1}{4}}\end{matrix}}T)\,} {\displaystyle =A\cdot \sin(2\pi f(t-{\begin{matrix}{\frac {1}{4}}\end{matrix}}T)+\theta )\,}
{\displaystyle =A\cdot \sin(2\pi ft-{\begin{matrix}{\frac {\pi }{2}}}\end{matrix}}+\theta ),\,}

a cărei „fază” este acum {\displaystyle \theta -{\begin{matrix}{\frac {\pi }{2}}\end{matrix}}}.} A fost decalată cu {\displaystyle {\begin{matrix}{\frac {\pi }{2}}\end{matrix}}}.

Diferența de fază

File:Sine waves same phase.svg

Unde în fază

File:Sine waves different phase.svg

Out-of-phase waves

File:Phase-shift illustration.png

Stânga: partea reală a unei unde plane care se deplasează de sus în jos. Dreapta: aceeași undă după ce o secțiune centrală a suferit o defazare, de exemplu, prin trecerea printr-o sticlă de grosime diferită față de celelalte părți. (Ilustrația din dreapta ignoră efectul de difracție al cărui efect crește la distanțe mari).

Două oscilatoare care au aceeași frecvență și faze diferite au o diferență de fază, iar oscilatoarele se spune că sunt defazate una față de cealaltă. Valoarea cu care astfel de oscilatoare sunt defazate unul față de celălalt poate fi exprimată în grade de la 0° la 360° sau în radiani de la 0 la 2π. Dacă diferența de fază este de 180 de grade (π radiani), atunci se spune că cele două oscilatoare sunt în antifază. Dacă două unde care interacționează se întâlnesc într-un punct în care sunt în antifază, atunci va avea loc o interferență distructivă. Este obișnuit ca undele de energie electromagnetică (lumină, RF), acustică (sunet) sau de altă natură să se suprapună în mediul lor de transmisie. Când se întâmplă acest lucru, diferența de fază determină dacă acestea se întăresc sau se slăbesc reciproc. Anularea completă este posibilă pentru undele cu amplitudini egale.

Timpul este uneori folosit (în loc de unghi) pentru a exprima poziția în cadrul ciclului unei oscilații.

  • O diferență de fază este analogă cu doi atleți care aleargă pe o pistă de curse cu aceeași viteză și în aceeași direcție, dar care pornesc din poziții diferite pe pistă. Ei trec pe lângă un punct la momente diferite în timp. Dar diferența de timp (diferența de fază) dintre ei este o constantă – aceeași pentru fiecare trecere, deoarece ei sunt la aceeași viteză și în aceeași direcție. Dacă ar avea viteze diferite (frecvențe diferite), diferența de fază ar reflecta doar poziții de plecare diferite.
  • Măsurăm rotația Pământului în ore, în loc de radiani. Și, prin urmare, fusurile orare sunt un exemplu de diferențe de fază.

Componentele în fază și în cuadratură (I&Q)

Termenul în fază este întâlnit și în contextul semnalelor de comunicație:

{\displaystyle A(t)\cdot \sin=I(t)\cdot \sin(2\pi ft)+Q(t)\cdot \sublinie {\cos(2\pi ft)} _{\sin \left(2\pi ft+{\begin{matrix}{\frac {\pi }{2}}}\end{matrix}}\right)}}

și:

{\displaystyle A(t)\cdot \cos=I(t)\cdot \cos(2\pi ft)\underbrace {-Q(t)\cdot \sin(2\pi ft)} _{+Q(t)\cdot \cos \left(2\pi ft+{\begin{matrix}{\frac {\pi }{2}}}\end{matrix}}\right)}}

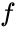
unde {\displaystyle f\,} reprezintă o frecvență purtătoare și

{\displaystyle I(t)\ {\stackrel {\mathrm {def} }{{=}}}\ A(t)\cdot \cos,\,}{\displaystyle Q(t)\ {\stackrel {\mathrm {\def} }{{=}}}\ A(t)\cdot \sin.\,}

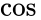
{\displaystyle A(t)\,} și {\displaystyle \phi (t)\,} reprezintă o posibilă modulație a unei unde purtătoare pure, de exemplu: {\displaystyle \sin(2\pi ft).\,} Modulația modifică componenta originală {\displaystyle \sin \,} a purtătoarei și creează o componentă (nouă) {\displaystyle \cos \,}, așa cum se arată mai sus. Componenta care este în fază cu purtătoarea originală se numește componentă în fază. Cealaltă componentă, care este întotdeauna la 90° ({\displaystyle {\begin{matrix}{\frac {\pi }{2}}}\end{matrix}}} radiani) „defazată”, se numește componentă în cuadratură.

Coerența de fază

Coerența este calitatea unei unde de a prezenta o relație de fază bine definită în diferite regiuni ale domeniului său de definiție.

În fizică, mecanica cuantică atribuie undele unor obiecte fizice. Funcția de undă este complexă și, deoarece modulul său pătrat este asociat cu probabilitatea de observare a obiectului, caracterul complex al funcției de undă este asociat cu faza. Deoarece algebra complexă este responsabilă de efectul de interferență izbitor al mecanicii cuantice, faza particulelor este, prin urmare, legată în ultimă instanță de comportamentul lor cuantic.

.

Lasă un răspuns

Adresa ta de email nu va fi publicată.