Rețeaua Bayesiană de Convingeri sau Rețeaua Bayesiană sau Rețeaua de Convingeri este un Model Grafic Probabilist (PGM) care reprezintă dependențele condiționate între variabile aleatoare printr-un Graf Aciclic Direcționat (DAG).

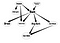
Astăzi, voi încerca să explic principalele aspecte ale Rețelelor de Credință, în special pentru aplicații care pot fi legate de Analiza Rețelelor Sociale(SNA). În plus, vă voi arăta un exemplu de implementare a acestui tip de rețea.

Pentru ce folosim Rețelele Bayesiene?

Rețelele Bayesiene sunt aplicate în multe domenii. De exemplu, diagnosticarea bolilor, căutarea optimizată pe web, filtrarea spam-ului, rețelele de reglementare genetică etc. Și această listă poate fi extinsă. Obiectivul principal al acestor rețele este încercarea de a înțelege structura relațiilor de cauzalitate. Pentru a clarifica acest lucru, să luăm în considerare o problemă de diagnosticare a unei boli. Având în vedere simptomele date și boala care rezultă din acestea, construim rețeaua noastră de convingeri și, atunci când apare un nou pacient, putem deduce ce boală sau ce boli poate avea noul pacient prin furnizarea de probabilități pentru fiecare boală. În mod similar, aceste relații de cauzalitate pot fi construite pentru alte probleme și se pot aplica tehnici de inferență pentru a obține rezultate interesante.

Revizuirea rapidă a probabilităților

Înainte de a continua, pentru a ne reîmprospăta memoria, permiteți-mi să vă dau definiția proprietății condiționale. Probabilitatea condiționată este probabilitatea unei variabile aleatoare atunci când este dată o altă variabilă aleatoare. Se arată prin

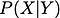
Dacă aceste două variabile aleatoare sunt dependente,

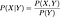
Dacă ele sunt independente, atunci

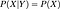
Definiția matematică a rețelelor de credință

Se calculează probabilitățile în rețelele de credință prin următoarea formulă

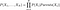
După cum ați înțeles din formulă, pentru a putea calcula distribuția comună trebuie să avem probabilitățile condiționate indicate de rețea. Dar, mai departe, dacă avem distribuția comună, atunci putem începe să ne punem întrebări interesante. De exemplu, în primul exemplu, întrebăm care este probabilitatea de „ploaie” dacă „SEZONUL” este „IARNA” și „Lătratul câinelui” este „ADEVĂRAT”.

Exemplu Python de Rețea de credință

Așa că, cred că este suficient pentru teorie și haideți să vedem un exemplu real cu limbajul meu preferat de programare actual, Python ❤️ Înainte de a continua, puteți găsi caietul Jupyter Notebook pe care l-am scris aici.

# create the nodes
season = BbnNode(Variable(0, 'season', ), )
atmos_pres = BbnNode(Variable(1, 'atmos_press', ), )
allergies = BbnNode(Variable(2, 'allergies', ), )
rain = BbnNode(Variable(3, 'rain', ), )
grass = BbnNode(Variable(4, 'grass', ), )
umbrellas = BbnNode(Variable(5, 'umbrellas', ), )
dog_bark = BbnNode(Variable(6, 'dog_bark', ), )
cat_mood = BbnNode(Variable(7, 'cat_mood', ), )
cat_hide = BbnNode(Variable(8, 'cat_hide', ), )bbn = Bbn() \
.add_node(season) \
.add_node(atmos_pres) \
.add_node(allergies) \
.add_node(rain) \
.add_node(grass) \
.add_node(umbrellas) \
.add_node(dog_bark) \
.add_node(cat_mood) \
.add_node(cat_hide) \
.add_edge(Edge(season, allergies, EdgeType.DIRECTED)) \
.add_edge(Edge(season, umbrellas, EdgeType.DIRECTED)) \
.add_edge(Edge(season, rain, EdgeType.DIRECTED)) \
.add_edge(Edge(atmos_pres, rain, EdgeType.DIRECTED)) \
.add_edge(Edge(rain, grass, EdgeType.DIRECTED)) \
.add_edge(Edge(rain, umbrellas, EdgeType.DIRECTED)) \
.add_edge(Edge(rain, dog_bark, EdgeType.DIRECTED)) \
.add_edge(Edge(rain, cat_mood, EdgeType.DIRECTED)) \
.add_edge(Edge(dog_bark, cat_hide, EdgeType.DIRECTED)) \
.add_edge(Edge(cat_mood, cat_hide, EdgeType.DIRECTED))

În primul rând am descris nodurile noastre cu probabilități condiționate. Ar trebui să observați că am sărit peste unele valori de stare posibile pentru simplitate. De exemplu, variabila sezonului ia alte valori „primăvară” și „toamnă”. Deci, ideea este aceeași.

Nu, să verificăm dacă rețeaua noastră este construită corect sau nu.

with warnings.catch_warnings():
warnings.simplefilter('ignore')
graph = convert_for_drawing(bbn)
pos = nx.nx_agraph.graphviz_layout(graph, prog='neato')plt.figure(figsize=(20, 10))
plt.subplot(121) 
labels = dict()
nx.draw(graph, pos=pos, with_labels=True, labels=labels)
plt.title('BBN DAG')

Acest fragment de cod ar rezulta următorul grafic

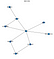
Așa că, vedeți că această rețea se potrivește cu desenul meu fantezist de la început. Acum, haideți să facem niște inferențe pe această rețea de credință.

# convert the BBN to a join tree
join_tree = InferenceController.apply(bbn)# insert an observation evidence
ev = EvidenceBuilder() \
.with_node(join_tree.get_bbn_node_by_name('season')) \
.with_evidence('winter', 1.0) \
.build()join_tree.set_observation(ev)# print the marginal probabilities
for node in join_tree.get_bbn_nodes():
potential = join_tree.get_bbn_potential(node)
print(node)
print(potential)
print('--------------------->')

Acest fragment de cod oferă, practic, dovezi pentru rețea conform cărora sezonul este iarna cu o probabilitate de 1,0. În funcție de aceste dovezi, atunci când facem inferența, obținem următoarele rezultate.

0|season|winter,summer
0=winter|1.00000
0=summer|0.00000
--------------------->
2|allergies|allergic,non_alergic
2=allergic|0.70000
2=non_alergic|0.30000
--------------------->
3|rain|rainy,sunny
3=rainy|0.80000
3=sunny|0.20000
--------------------->
4|grass|grass,no_grass
4=grass|0.70000
4=no_grass|0.30000
--------------------->
1|atmos_press|high,low
1=high|0.50000
1=low|0.50000
--------------------->
5|umbrellas|on,off
5=on|0.95200
5=off|0.04800
--------------------->
6|dog_bark|bark,not_bark
6=bark|0.66000
6=not_bark|0.34000
--------------------->
7|cat_mood|good,bad
7=good|0.23000
7=bad|0.77000
--------------------->
8|cat_hide|hide,show
8=hide|0.87150
8=show|0.12850
--------------------->

Când adăugăm alte dovezi, cum ar fi faptul că câinele nu latră

# convert the BBN to a join tree
join_tree = InferenceController.apply(bbn)# insert an observation evidence
ev = EvidenceBuilder() \
.with_node(join_tree.get_bbn_node_by_name('season')) \
.with_evidence('winter', 1.0) \
.build()ev2 = EvidenceBuilder() \
.with_node(join_tree.get_bbn_node_by_name('dog_bark')) \
.with_evidence('not_bark', 1.0) \
.build()join_tree.set_observation(ev)
join_tree.set_observation(ev2)# print the marginal probabilities
for node in join_tree.get_bbn_nodes():
potential = join_tree.get_bbn_potential(node)
print(node)
print(potential)
print('--------------------->')

obținem următoarele rezultate ale inferenței

0|season|winter,summer
0=winter|1.00000
0=summer|0.00000
--------------------->
2|allergies|allergic,non_alergic
2=allergic|0.70000
2=non_alergic|0.30000
--------------------->
3|rain|rainy,sunny
3=rainy|0.47059
3=sunny|0.52941
--------------------->
4|grass|grass,no_grass
4=grass|0.53529
4=no_grass|0.46471
--------------------->
1|atmos_press|high,low
1=high|0.39706
1=low|0.60294
--------------------->
5|umbrellas|on,off
5=on|0.88941
5=off|0.11059
--------------------->
6|dog_bark|bark,not_bark
6=bark|0.00000
6=not_bark|1.00000
--------------------->
7|cat_mood|good,bad
7=good|0.52647
7=bad|0.47353
--------------------->
8|cat_hide|hide,show
8=hide|0.83162
8=show|0.16838
--------------------->

Vezi diferența? 😆 O mulțime de valori ale probabilității s-au schimbat atunci când adăugăm dovezile legate de lătrat. Este cu siguranță un exemplu prostesc, dar este frumos pentru a obține o intuiție.

Cum se utilizează rețelele bayesiene în SNA?

Rețelele bayesiene sunt instrumente foarte puternice pentru a înțelege structura relațiilor de cauzalitate între variabile. Odată ce ați proiectat modelul, chiar și cu un set mic de date, acesta vă poate spune diverse lucruri. Întrebarea din această parte este cum se poate beneficia de Rețelele Bayesiene în SNA. Răspunsul nu este unic, dar să începem cu o idee profundă. În SNA, încercăm să înțelegem structura unei rețele sociale. În plus, încercăm să înțelegem importanța nodurilor. Dar nu știm care sunt rezultatele măsurătorilor noastre de importanță. Acesta este punctul în care au loc rețelele bayesiene. De exemplu, dacă credeți că importanța unui nod este cauzată de Degree Centrality și Link Centrality, este posibil să aveți următoarea rețea:

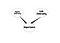
Aceasta este o rețea bayesiană foarte naivă. În plus față de determinarea importanței nodurilor, o aplicație ulterioară poate fi căutarea unor tipuri specifice de noduri. Să luăm în considerare o rețea socială în care există câteva persoane care sunt potențiali lideri și pe care doresc să le caut. Să considerăm următorul graf

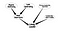
Această rețea un pic mai complicată ne va ajuta să determinăm incertitudinea nodurilor legate de a fi un lider.

O altă aplicație ar fi deducerea legăturilor. Noile legături pot fi deduse din cele existente. De exemplu, din apartenența la un grup într-o rețea socială, poate fi dedusă legătura de apartenență probabilă. Ceea ce am vrut să spun este că putem modela o nouă legătură între utilizatori și grupuri prin luarea în considerare a legăturilor existente. A se vedea următoarea diagramă a modelului

Acum, acestea sunt câteva exemple de bază ale modului în care rețelele bayesiene pot fi aplicate în SNA. Acest subiect nu este studiat foarte bine, dar cred că ar putea fi foarte util să fie studiat în continuare.

Concluzie

Ceea ce este greu la Rețelele Bayesiene este proiectarea. În special, când te gândești la SNA, a construi o cartografiere din Rețeaua Socială cu o Rețea Bayesiană este mai mult artă decât știință 😃 Dar odată ce ai făcut treaba de artă și ți-ai proiectat modelul foarte bine, aceste instrumente la îndemână îți pot spune o mulțime de lucruri. După cum știm, rețelele bayesiene sunt aplicate în tipuri vaste de domenii. A funcționat foarte bine în majoritatea cazurilor. Prin urmare, cred cu tărie că putem face inferențe foarte profunde și în cazul rețelelor sociale.

Pentru investigații suplimentare cu SNA și rețelele bayesiene, vă rugăm să rămâneți pe recepție 🚀

.