Clasificarea este o abordare de învățare automată supravegheată, în care algoritmul învață din datele de intrare care îi sunt furnizate – și apoi folosește această învățare pentru a clasifica noile observații.
Cu alte cuvinte, setul de date de instruire este utilizat pentru a obține condiții limită mai bune care pot fi folosite pentru a determina fiecare clasă țintă; odată ce aceste condiții limită sunt determinate, următoarea sarcină este de a prezice clasa țintă.
Clasificatorii binari lucrează cu doar două clase sau rezultate posibile (exemplu: sentiment pozitiv sau negativ; dacă creditorul va plăti sau nu împrumutul; etc.), iar clasificatorii multiclasă lucrează cu clase multiple (exemplu: cărei țări îi aparține un steag, dacă o imagine este un măr, o banană sau o portocală; etc.). Multiclasa presupune că fiecare eșantion este atribuit unei singure etichete.

Unul dintre primii algoritmi populari de clasificare în învățarea automată a fost Naive Bayes, un clasificator probabilistic inspirat de teorema lui Bayes (care ne permite să facem deducții raționale ale evenimentelor care se întâmplă în lumea reală pe baza cunoașterii prealabile a observațiilor care o pot implica). Numele („Naive”) provine de la faptul că algoritmul presupune că atributele sunt condițional independente.
Algoritmul este un algoritm simplu de implementat și reprezintă, de obicei, o metodă rezonabilă pentru a da startul eforturilor de clasificare. Se poate adapta cu ușurință la seturi de date mai mari (durează un timp liniar față de aproximarea iterativă, așa cum se utilizează pentru multe alte tipuri de clasificatoare, care este mai costisitoare din punct de vedere al resurselor de calcul) și necesită o cantitate mică de date de instruire.
Cu toate acestea, Naive Bayes poate suferi de o problemă cunoscută sub numele de „problema probabilității zero”, atunci când probabilitatea condiționată este zero pentru un anumit atribut, nereușind să furnizeze o predicție validă. O soluție este de a utiliza o procedură de netezire (ex: metoda Laplace).

P(c|x) este probabilitatea posterioară a clasei (c, țintă) dat fiind predictorul (x, atribute). P(c) este probabilitatea anterioară a clasei. P(x|c) este verosimilitatea care reprezintă probabilitatea predictorului dată de clasă, iar P(x) este probabilitatea anterioară a predictorului.
Primul pas al algoritmului constă în calcularea probabilității anterioare pentru etichetele de clasă date. Apoi, găsirea probabilității de probabilitate cu fiecare atribut, pentru fiecare clasă. Ulterior, punând aceste valori în formula Bayes & se calculează probabilitatea posterioară și apoi se vede care clasă are o probabilitate mai mare, având în vedere că intrarea aparține clasei cu probabilitate mai mare.
Este destul de simplu să se implementeze Naive Bayes în Python prin utilizarea bibliotecii scikit-learn. Există, de fapt, trei tipuri de modele Naive Bayes în cadrul bibliotecii scikit-learn: (a) tipul Gaussian (presupune că caracteristicile urmează o distribuție normală, de tip clopot), (b) Multinomial (utilizat pentru numărători discrete, în termeni de cantitate de ori un rezultat este observat pe parcursul a x încercări) și (c) Bernoulli (util pentru vectori de caracteristici binare; un caz de utilizare popular este clasificarea textului).
Un alt mecanism popular este Arborele de decizie. Date fiind o serie de date de atribute împreună cu clasele sale, arborele produce o secvență de reguli care pot fi utilizate pentru a clasifica datele. Algoritmul împarte eșantionul în două sau mai multe seturi omogene (frunze) pe baza celor mai semnificative diferențieri din variabilele de intrare. Pentru a alege un diferențiator (predictor), algoritmul ia în considerare toate caracteristicile și face o împărțire binară a acestora (pentru datele categorice, se împarte în funcție de cat; pentru cele continue, se alege un prag de tăiere). Apoi îl va alege pe cel cu cel mai mic cost (adică cea mai mare acuratețe), repetând recursiv, până când reușește să divizeze cu succes datele în toate frunzele (sau atinge adâncimea maximă).
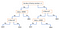
Arborii de decizie sunt, în general, simplu de înțeles și de vizualizat, necesitând puțină pregătire a datelor. De asemenea, această metodă poate gestiona atât date numerice, cât și categorice. Pe de altă parte, arborii complecși nu generalizează bine („supraadaptare”), iar arborii de decizie pot fi oarecum instabili, deoarece mici variații în date ar putea duce la generarea unui arbore complet diferit.
O metodă de clasificare care derivă din arborii de decizie este Random Forest, în esență un „metaestimator” care potrivește un număr de arbori de decizie pe diferite subeșantioane de seturi de date și utilizează media pentru a îmbunătăți precizia predictivă a modelului și controlează supraadaptarea. Dimensiunea subeșantioanelor este aceeași cu dimensiunea eșantionului inițial de intrare – dar eșantioanele sunt extrase cu înlocuire.
Random Forests tind să prezinte un grad mai mare de robustețe la supraajustare (>robustețe la zgomotul din date), cu un timp de execuție eficient chiar și în seturi de date mai mari. Totuși, ele sunt mai sensibile la seturi de date dezechilibrate, fiind, de asemenea, puțin mai complexe de interpretat și necesitând mai multe resurse de calcul.
Un alt clasificator popular în ML este Regresia Logistică – unde probabilitățile care descriu posibilele rezultate ale unui singur proces sunt modelate folosind o funcție logistică (metodă de clasificare în ciuda numelui):

Iată cum arată ecuația logistică:
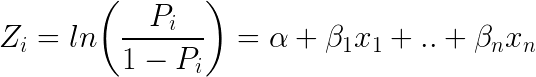
Să luăm e (exponentul) de ambele părți ale ecuației rezultă:
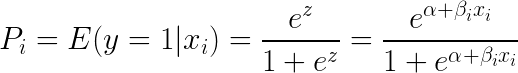
Regresia logistică este cea mai utilă pentru a înțelege influența mai multor variabile independente asupra unei singure variabile de rezultat. Este axată pe clasificarea binară (pentru probleme cu clase multiple, se utilizează extensii ale regresiei logistice, cum ar fi regresia logistică multinomială și ordinală). Regresia logistică este populară în toate cazurile de utilizare, cum ar fi analiza creditării și propensiunea de a răspunde/cumpăra.
În sfârșit, kNN (pentru „k Nearest Neighbors”) este, de asemenea, adesea utilizat pentru probleme de clasificare. kNN este un algoritm simplu care stochează toate cazurile disponibile și clasifică noile cazuri pe baza unei măsuri de similaritate (de exemplu, funcții de distanță). A fost utilizat în estimarea statistică și recunoașterea modelelor încă de la începutul anilor 1970 ca o tehnică neparametrică:


.