(IUCr) Simboluri pentru elemente de simetrie

Acta Cryst. (1992). A48, 727-732

Raportul final al Comitetului ad-hoc al Uniunii Internaționale de Cristalografie privind nomenclatura simetriei*

De P. M. DE WOLFF (președinte), Meermanstraat 126, 2614 AM Delft, Olanda,

Y. BILLIET, Ecole Nationale d’Ingénieurs, BPW 3038 Sfax, Tunesië,

J. D. H. DONNAY, Department of Geological Sciences, McGill University, 3450 University Street, Montreal, Canada H3A 2A7,

W. FISCHER, Institut für Mineralogie, Petrologie und Kristallographie der Phillips-Universität, Lahnberge, D-3550 Marburg (Lahn), Germania,

R. B. GALIULIN, Institute of Crystallography, Academy of Sciences of Russia, Leninsky Prospekt 59, Moscova 117333, Rusia,

A. M. GLAZER, Clarendon Laboratory, University of Oxford, Parks Road, Oxford OX1 3PU Anglia,

TH. HAHN, Institut für Kristallographie, RWTH, Templergraben 55, D-5100 Aachen, Germania,

MARJORIE SENECHAL, Department of Mathematics, Smith College, Northampton, MA 01063, SUA,

D. P. SHOEMAKER, Chemistry Department, Oregon State University, OR 97331, SUA,

H. WONDRATSCHEK, Institut für Kristallographie, Universität Karlsruhe, Kaiserstrasse 12, D-7500 Karlsruhe 1, Germania,

A. J. C. WILSON (ex officio, IUCr Commission on International Tables), Crystallographic Data Centre, University Chemistry Laboratory, Lensfield Road, Cambridge CB2 1EW, Anglia

AND S. C. C. ABRAHAMS (ex officio, IUCr Commission on Crystallographic Nomenclature), Department of Physics, Southern Oregon State College, 1250 Siskiyou Boulevard, Ashland, OR 97520-5047, USA

(Primit la 7 noiembrie 1991; acceptat la 9 martie 1992)

* Numit la 14 noiembrie 1984, modificat la 10 august 1987 conform regulilor de bază prezentate în Acta Cryst. (1979), A35, 1072. Raport final acceptat la 23 decembrie 1991 de către Comisia de Nomenclatură Cristalografică a IUCr și la 9 martie 1992 de către Comitetul Executiv.

Abstract

Sunt propuse simboluri tipărite noi sau redefinite în lumina redefinirii recent acceptate a elementelor de simetrie . În special, litera e acoperă anumite planuri de planare care până acum nu aveau un simbol unic, cum ar fi cele numite „fie a, fie b”. Se recomandă utilizarea literei e în simbolul Hermann-Mauguin pentru cinci grupuri spațiale diferite. Pentru planurile e proiectate într-o direcție paralelă cu planul, se propune un simbol grafic care elimină ambiguitatea denumirii lor actuale. Litera k este propusă pentru o clasă nou definită de planuri de planare, care până acum nu aveau un simbol specific. Simbolurile pentru operațiile de simetrie introduse în descrierile grupurilor spațiale din Tabelele Internaționale de Cristalografie (1989), Vol. A (Dordrecht: Kluwer Academic Publishers) sunt recomandate pentru utilizare generală, cu modificări doar pentru operațiile de reflexie a planurilor de alunecare.

Introducere

Comitetul ad-hoc numit în 1980 pentru a examina „problemele de nomenclatură privind operațiile de simetrie și elementele de simetrie în grupurile spațiale” a publicat două rapoarte intitulate Nomenclature for Crystal Families, Bravais-Lattice Types and Arithmetic Classes (de Wolff et al., 1985) și Definition of Symmetry Elements in Space Groups and Point Groups (de Wolff et al., 1989). După cum se menționează în raportul din 1989, singura problemă nerezolvată în ceea ce privește operațiile de simetrie este aceea a alegerii simbolurilor adecvate, deoarece conceptul este clar. O notație provizorie a fost adoptată în Tabelele Internaționale de Cristalografie (1983, 1989), denumită în continuare ITA83.

Simboluri tipărite pentru elementele de simetrie

Definiția elementelor de simetrie, așa cum a fost dată în Raportul din 1989 (de Wolff et al.), va fi utilizată pe parcursul prezentului Raport. Aici repetăm esența:

Pentru orice operație de simetrie dată se definește elementul său geometric (plan, punct și/sau linie). Un element de simetrie este combinația dintre elementul geometric al uneia dintre operațiile de simetrie dintr-un anumit grup spațial cu setul (numit `set de elemente’) al tuturor operațiilor de simetrie din acel grup spațial care au în comun acest element geometric.

Definițiile explicite ale elementelor geometrice și descrierile elementelor de simetrie care rezultă, precum și simbolurile acestora sunt prezentate în tabelele 1 și 2. (Acestea sunt identice cu tabelele 1 și 2 din Raportul din 1989, cu excepția planurilor de alunecare și sunt repetate aici pentru a fi complete, a se vedea mai jos). Fiecare element de simetrie este reprezentat de un simbol format din două caractere. Primul caracter este un E majuscul pentru toate elementele de simetrie. Acesta are rolul de a arăta că simbolul se referă la un element de simetrie și nu, de exemplu, la o operație de simetrie. În cazul în care acest lucru este deja clar din context, atunci E-ul poate fi omis, de exemplu „o axă 2” în loc de „o axă E2”.

Tabelul 1. Elemente geometrice ale operațiilor de simetrie în grupuri de puncte și grupuri spațiale
Operație de simetrie	Element geometric	Parametri suplimentari
Identitate	Nu este necesar	Nimic
Traducere	Nu este necesar	Vector $\mathbf{t}$ .
Reflecție în planul A	Planul A	Nimic
Reflecție în alunecare =reflecție în planul A și translație $\mathbf{v}$ paralel cu A	Planul A	Vector de alunecare $\mathbf{v}$
Rotație în jurul liniei b	Linia b	Unghiul și sensul de rotație
Rotația șurubului = rotație în jurul liniei b și translație $\mathbf{u}$ paralelă cu b	Linia b	Unghiul și sensul vectorului de rotație a șurubului $\mathbf{u}$
Rotoinversie = rotație în jurul liniei b și inversie prin punctul P pe b	Linia b și punctul P pe b	Unghiul (care nu este egal cu $\pi$ ) și sensul de rotație
Inversie prin punctul P	Punctul P	Nimic

Simbolul Eg enumerat în Raportul din 1989 poate fi utilizat pentru planurile de planare dacă se dorește doar să se arate că elementul de simetrie este un plan de planare. Pe de altă parte, dacă aparține unuia dintre tipurile speciale care au fost de mult timp notate cu o literă corespunzătoare (a, b, c, n sau d; cf. ITA83), atunci acea literă înlocuiește g în Eg.

Tabelul 2. Elemente de simetrie în grupuri de puncte și grupuri spațiale
Numele elementului de simetrie	Simbol	Element geometric	Operație de definire (d.o.)	Operații în setul de elemente
Plan de oglindă	Em	Plan A	Reflecție în A	D.o. și echivalentele sale coplanare*
Plan de alunecare	Eg $\ddag$	Plan A	Reflexie în A, 2v (nu v) o translație de rețea	D.o. și echivalentele sale coplanare*
Axa de rotație	En	Linia b	Rotație în jurul lui b, unghiul $2\pi/n$ ,n = 2, 3, 4 sau 6	1-a, $\puncte$ ,(n – 1)-lea puteri ale d.o. și echivalentele lor coaxiale\dag
Axa șurubului	Enj	Linia b	Rotația șurubului în jurul lui b, unghiul $2\pi/n$ , u =j/n ori cea mai scurtă translație a rețelei în lungul lui b, șurubul din dreapta; n = 2, 3, 4 sau 6, $j=1,\dots,(n-1)$	1-a, $\dots$ ,(n – 1)a putere a lui d.o. și echivalentele lor coaxiale\dag
Axa de rotoinversie	$E\bar n$	Linia b și punctul P pe b	Rotoinversie: rotație în jurul lui b, unghiul $2\pi/n$ , și inversiune prin P; n = 3, 4 sau 6	D.o. și inversa sa
Centru	$E\bar 1$	Punctul P	Inversie prin P	D.o. numai

* Adică toate reflexiile glisante cu același plan de reflexie, cu vectori glisanți care diferă de cel al d.o. (considerat zero pentru o reflexie) cu un vector de translație a rețelei.
\dag Ceea ce înseamnă toate rotațiile și rotațiile de șurub cu aceeași axă b, același unghi și sens de rotație și același vector de șurub $\mathbf{u}$ (zero pentru o rotație) până la un vector de translație a rețelei.
$\ddag$ În Eg, g este înlocuit cu a, b, c, n, d, e sau k pentru tipuri specifice de planuri de alunecare, cf. §2.

Un nou aspect important al simbolurilor ca Eb poate fi totuși subliniat. Conform ITA83, desemnarea unui plan prin b însemna pur și simplu că o reflexie de alunecare în plan cu o componentă de alunecare b/2 de-a lungul axei b este o operație de simetrie. Această definiție se aplică cu siguranță situației reprezentate în Fig. 1.

Fig. 1. (După W. Fischer.) Setul de elemente al unui plan Eb-glide, reprezentat ca un set de puncte deasupra (+) și dedesubtul (-) planului produs de reflexiile de glisare în plan, pornind, de exemplu, de la semnul + din stânga sus. Rețeaua N de translații paralele cu planul (+ $\cdots$ + vectori) este indicată de o plasă, care în acest caz se întâmplă să fie dreptunghiulară. Ambele perechi de muchii sunt paralele cu axele cristalelor. Există o reflexie de alunecare cu vectorul său de alunecare (+ $\cdots$ -) de-a lungul axei b.

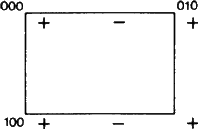
$\begin{figure} \includegraphics {fig1.ps} \end{figure}$

Figura 1 este adaptată, la fel ca și figurile 2 și 3, dintr-un set de figuri similare concepute de W. Fischer, membru al Comitetului Ad-hoc, ca inventar al tuturor tipurilor de planare. Deși setul a fost prezentat comitetului în 1980, cu mult înainte de publicarea raportului din 1989, fiecare dintre figurile sale arată exact „setul de elemente” al planului de planare, așa cum a fost definit în acel raport (a se vedea rezumatul de mai sus). Pentru un plan de planare, setul de elemente este format din toate reflexiile de planare care au planul ca element geometric comun. Acțiunea lor este prezentată în proiecție pe acest plan. De la poziția de plecare a oricărui semn +, fiecare semn – rezultă din una dintre reflexiile de alunecare din set. Toate acestea sunt reprezentate în cadrul unei ochiuri elementare a modelului periodic bidimensional de semne + și – rezultat.

Ne vom referi adesea la rețeaua N formată de toate translațiile paralele cu planul; această rețea este ușor de vizualizat dacă ne uităm doar la semnele +. Acești vectori trebuie deosebiți net de vectorii care leagă un semn + de orice semn -, fiecare dintre aceștia fiind vectorul de alunecare al unei reflexii de alunecare aparținând setului de elemente.

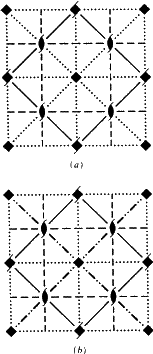
Noiul aspect apare deoarece, în unele cazuri, prin definiția ITA83, planul de alunecare b este și un plan de alunecare a-; vezi Fig. 2. În mod evident, acest lucru se întâmplă numai dacă rețeaua N este centrată ortogonal, deoarece atunci glisarea a poate fi transformată în glisarea b (și invers) prin adăugarea unei translații de centrare. Practica de până acum a fost de a numi în mod arbitrar un astfel de plan de alunecare fie a, fie b, provocând astfel o prejudecată nejustificată și o lipsă de unicitate a acestor simboluri. Prin urmare, propunem ca cazul din figura 2 să fie acoperit de un simbol separat.

Fig. 2. (După W. Fischer.) Setul de elemente al unui plan Ee-glide. Cf. legenda de la Fig. 1. Observați că rețeaua N de aici este centrată ortogonal.

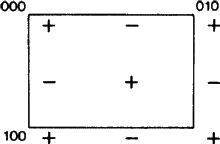
$\begin{figure} \includegraphics {fig2.ps} \end{figure}$

Scopul acestui simbol ar trebui apoi extins la planurile de alunecare într-o orientare diagonală, adică paralel cu o singură axă a cristalului, cu condiția ca planul de alunecare să aibă un vector de alunecare de-a lungul acelei axe și ca rețeaua N să fie centrată ortogonal. Pentru astfel de planuri nu există ambiguitatea alegerii aleatorii a-b de mai sus, dar domeniul de aplicare extins al noului simbol este în concordanță cu cel al tuturor simbolurilor existente (și anume a, b, c, n și d). Fiecare dintre acestea este utilizat pentru un plan de alunecare cu una și două axe de cristal în rețeaua N, cf. Fig. 3.

Se propune litera e pentru noul simbol. Astfel, Ee se va aplica planurilor de alunecare cu plase ortogonale centrate N și cu cel puțin un vector de alunecare de-a lungul unei axe cristaline. Prin urmare, este necesar un nou criteriu: și anume orientarea vectorilor de planare în raport cu axele convenționale ale cristalului. Deoarece acestea din urmă se află de-a lungul direcțiilor de simetrie, în timp ce fiecare plan de alunecare este paralel cu un plan oglindă al rețelei, nu este surprinzător faptul că există întotdeauna cel puțin o axă convențională a cristalului în N. Dacă există doar o astfel de axă, atunci perpendicular pe ea există întotdeauna o altă translație în N.

Noul simbol e, precum și vechile simboluri a, b, c, d, n vor fi acum redefinite în funcție de acest nou criteriu și de tipul de rețea Bravais N. Această rețea este monoclinică sau ortogonală sau tetragonală primitivă (mp sau op sau tp) sau ortogonală centrată (oc). Numai rețelele de tip oc N permit un plan de alunecare Ee-glide. Simbolul En se aplică rețelelor N de tip Bravais mp sau op, în timp ce Ed se aplică rețelelor N de tip oc. (După cum se menționează într-o notă de subsol la tabelul 1.3 din ITA83: „Planurile de alunecare d apar numai în grupurile spațiale ortorombice F, în grupurile spațiale tetragonale I și în grupurile spațiale cubice I și F.”. Ele apar întotdeauna în perechi cu vectori de alunecare alternativi”). Spre deosebire de planurile Ea, Eb, Ec și Ee, însă, pentru planurile En și Ed nu există un vector de alunecare nici paralel, nici perpendicular pe o axă convențională în N.

Definițiile ulterioare ale planurilor de alunecare de tipurile de mai sus sunt rezumate în liniile (i) și (ii) din tabelul 3 și, mai explicit, în figura 3.

Tabelul 3. Simboluri tipărite pentru tipurile speciale de plane de planare
Numărul de vectori de alunecare paraleli sau perpendiculari pe axele cristalului în rețeaua N	Tipul Bravais al rețelei N
Simbolul este determinat de două criterii. Un criteriu este tipul Bravais (mp, op, tp sau oc) al rețelei N formată de translațiile de simetrie paralele cu planul considerat. Această rețea conține întotdeauna cel puțin o axă convențională a cristalului.* Celălalt criteriu se referă la orientarea vectorilor de alunecare în raport cu aceste axe.
	m, op, tp	oc
(i) Unul sau două	Ec(Ea, Eb)	Ee
(ii) Nici una paralelă, nici una perpendiculară	En	Ed
(iii) Nici una paralelă, una perpendiculară	Ek	–

* Așa cum este definit în ITA83, § 9.1; cu toate acestea, pentru grupurile spațiale romboedrice, aici se folosesc doar axele hexagonale.

Toate avioanele de planare rămase au fost anterior fără simbol specific. Fiecare dintre ele are o orientare diagonală (doar o axă convențională a cristalului în rețeaua N). Dintre reflexiile de alunecare din setul lor de elemente, nu există niciunul cu un vector de alunecare de-a lungul acestei axe. Cu toate acestea, un vector de alunecare este (prin simetrie) perpendicular pe ea. Un simbol pare de dorit, așa că se propune din nou o nouă literă: k. Noul simbol Ek este definit pe scurt în rândul (iii) din tabelul 3 și este ilustrat complet în blocul inferior al fig. 3. Câteva exemple sunt prezentate în §2.

Fig. 3. (Adaptat după desenele lui W. Fisher.) Toate aspectele posibile ale seturilor de elemente ale planurilor de planare reprezentate ca în Fig. 1, dar independent de etichetele axelor. Diagramele sunt grupate în coloane conduse de simbolul de tip Bravais-net (linia de sus) al rețelelor lor N, cf. Tabelul 3. Celelalte criterii din acest tabel se verifică privind mai întâi liniile duble care indică direcțiile axelor cristalelor în plan. O muchie (verticală) a ochiului de plasă N indicat este întotdeauna aleasă de-a lungul unei astfel de axe. Cealaltă muchie este orizontală, cu excepția cazurilor (1) și (8). Pentru diagramele (1), $\dots$ ,(5), simbolul planului de alunecare este eticheta a, b sau c a axei verticale; pentru celelalte, este litera încercuită din blocul conturat care conține diagrama. Observați vectorii de planare verticali în diagramele (1), $\dots$ ,(7), cei orizontali în (6), (7), (14), (15) și absența acestora în (8), $\dots$ ,(13). Un exemplu de apariție este dat sub fiecare diagramă prin simbolul grupului spațial și tripleta de coordonate a planului.

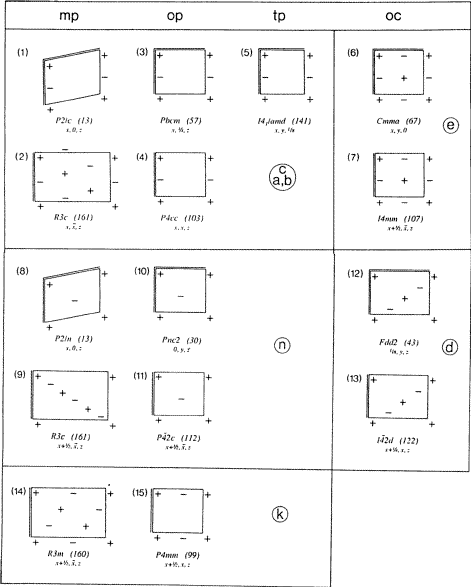
$\begin{figure} \includegrafica {fig3.ps} \end{figure}$

În Fig. 3, inventarul lui Fischer al tuturor tipurilor de plan de alunecare este prezentat într-o manieră prescurtată – deși încă completă – în care s-a dat mai multă importanță grafică axelor cristaline. Pentru fiecare diagramă, este listat un exemplu de apariție a acesteia într-o grupă spațială.

În unele grupe spațiale romboedrice, planurile Ec, En și Ek orientate diagonal apar cu rețele de tip mp N care pot fi descrise prin centrarea triplă a unei rețele ortogonale. O plasă triplă dreptunghiulară a rețelei N este prezentată pentru aceste tipuri de planuri de alunecare în Fig. 3, diagramele (2), (9) și (14). În diagrama (9), se recunoaște similitudinea cu alte diagrame n, cum ar fi (8) sau (10), dacă în (9) se consideră o plasă primitivă monoclinală a plasei N cu vectori de glisare diagonali.

Simboluri grafice pentru elementele de simetrie

Simbolurile grafice existente, așa cum au fost definite și utilizate în ITA83, sunt considerate adecvate de către Comitetul Ad-hoc, cu o singură excepție. Situația este foarte diferită de cea a simbolurilor tipărite, deoarece în desene direcția de proiecție devine un parametru adăugat. În termenii „proiecție perpendiculară” și „proiecție paralelă” utilizați mai jos, perpendicular și paralel se referă la orientarea direcției de proiecție în raport cu planul de planare.

Pentru un plan Ee există simbolul pentru proiecția perpendiculară a acestuia. Cu toate acestea, simbolurile grafice existente pentru proiecția paralelă a unui plan de alunecare Ee suferă de aceeași ambiguitate ca și simbolurile tipărite. Ele exprimă vectorul de alunecare fie paralel, fie perpendicular pe direcția de proiecție, dar alegerea este arbitrară. Prin urmare, se propune un nou simbol pentru proiecția paralelă a unui plan de alunecare Ee, și anume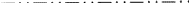

Exemple de planuri Ee.

Toate planurile de alunecare paralele la două axe din grupele spațiale Fmm2, Fmmm, $Fm\bar 3$ , $Fm\bar 3m$ și $Fm\bar 3c$ (nr. 42, 69, 202, 225 și 226), precum și anumite planuri din cele cinci grupe spațiale enumerate în §3.

Plani Ee orientați diagonic apar în grupele spațiale I4mm, I4cm, $I\bar 42m$ , I4/mmm, I4/mcm, $I\bar 43m$ și $Im\bar 3m$ (nr. 107, 108, 121, 121, 139, 140, 217 și 229).

În ITA83 toate aceste planuri Ee sunt desenate destul de arbitrar ca linii punctate sau punctate în proiecțiile lor paralele. Fig. 4 prezintă diagrama grupului spațial I4cm (nr. 108), atât așa cum apare în ITA83, cât și cu utilizarea noului simbol.

Fig. 4. (a) Diagrama grupului spațial I4cm (nr. 108) preluată din ITA83. (b) Aceeași, modificată prin utilizarea simbolului grafic propus în § 2, pentru proiecția paralelă a unui plan Ee.

$\begin{figure} \includegraphics {fig4.ps} \end{figure}$

Deși Ek este un nou simbol de tipar, în diagramele din ITA83 toate planele de planare Ek au fost desenate în mod satisfăcător cu aceleași convenții ca și cele folosite pentru planele de planare Ea/b/c. Ca și în aceste cazuri, există un singur vector de alunecare special (perpendicular pe axa cristalului în rețeaua N, cf. Tabelul 3). Atunci când acest vector este, de exemplu, paralel cu planul de proiecție, planul Ek este întotdeauna desenat ca linia punctată prescrisă de convenția relevantă. Prin urmare, nu se propune un nou simbol grafic pentru planurile de alunecare Ek.

Exemple de planuri Ek.

Aceste planuri sunt ușor de găsit în diagramele din ITA83 ca planuri paralele cu o singură axă și proiectate ca linii punctate, de exemplu xxz în P4bm și $P\bar 42_1m$ (nr. 100 și 113). În special, tabelul 3 este exact în conformitate cu distincția prezentată între planurile Ek și En. A se vedea, de exemplu, liniile punctate și punctiforme pentru R3m și R3c (nr. 160 și 161).

Simbolurile grupurilor spațiale Hermann-Mauguin

Caracterele care apar după litera de rețea în simbolul Hermann-Mauguin (HM) al unui grup spațial au fost inițial menite să reprezinte operații generatoare ale grupului. De exemplu, b era o reflexie b-glidă într-un plan orientat în funcție de poziția sa în simbolul HM.

În practică, elementele de simetrie populare, deși prost definite, au luat locul operațiilor. Astfel, b a ajuns să fie văzut ca un plan de glisare, Eb în terminologia noastră actuală. Nu este nici un rău în această reinterpretare, cu excepția cazului în care operația aparține unui plan de alunecare Ee-. Dacă acest lucru este valabil, de exemplu, pentru reflecția b-glide de mai sus, atunci există un plan Ee, dar nu și un plan Eb-glide în orientarea corespunzătoare. În acest caz, b devine un caracter foarte înșelător. În afară de aceasta, prejudecata (dată lui b în detrimentul lui a sau c) este la fel de deranjantă ca și în cazul simbolurilor elementelor de simetrie tratate în §1.

De aceea, se propune înlocuirea acestor litere înșelătoare a sau b cu e în toate cele cinci simboluri HM în care apar:

Grupa spațială nr.	39	41	64	67	68
Simbol în ITA83:	Abm2	Aba2	Cmca	Cmma	Ccca
Simbol nou:	Aem2	Aea2	Cmce	Cmme	Ccce.

Un alt avantaj al noilor simboluri propuse este că e – spre deosebire de a sau b – este neutru și, prin urmare, nu se modifică la permutarea axei.

Simboluri tipărite pentru operații de simetrie

Un set complet de simboluri tipărite a fost conceput de W. Fischer & E. Koch (ITA83, §11.2) și a fost aplicat pe scară largă în secțiunile Operații de simetrie din descrierile grupurilor spațiale.

În rezumat, fiecare simbol constă din până la trei părți. Prima parte este un singur caracter (uneori cu un indice) care descrie tipul de operație. Următoarea (următoarele) parte(e) oferă componentele oricărui vector de deplasare sau translație relevant – întotdeauna în paranteze – și coordonatele elementului geometric al operației, în această ordine.

Comitetul ad-hoc, după ce a analizat acest sistem, dorește să introducă două modificări pentru reflexiile de glisare:

(i) în loc de primul caracter actual (care poate fi a, b, c, n, d sau g), scrieți întotdeauna litera g;

(ii) scrieți întotdeauna componentele vectorului de glisare (în paranteze) în întregime, în special pentru reflexiile de glisare simple în planurile de glisare a-, b- sau c-, unde acestea erau omise anterior.

Regula (i) suprimă informațiile despre tipul de plan de alunecare căruia îi aparține operația. Foarte adesea aceste informații sunt irelevante sau chiar confuze. Pentru planurile a/b/c, suprimarea poate distruge informații esențiale, dar pierderea este refăcută de regula (ii), așa cum se arată în exemplul de mai jos.

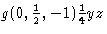Prin adoptarea acestor modificări, uniformitatea simbolurilor – și în ceea ce privește cele pentru rotații – este mult îmbunătățită. De exemplu, simbolul reflexiei prin alunecare în plan $x = \frac{1}{4}$ , cu vectorul de alunecare neobișnuit $(0, \frac{1}{2}, -1)$ , și anume $g(0, \frac{1}{2}, 1) \frac{1}{4}yz$ , se aliniază acum cu cel pentru o simplă reflexie prin alunecare b. În ITA83 aceasta din urmă a fost notată cu $b \frac{1}{4} y z$ , dar aceasta este schimbată prin regula (ii) în $g(0, \frac{1}{2}, 0) \frac{1}{4} y z$ .

Regula de mai sus se aplică în egală măsură reflexiilor de alunecare aparținând setului de elemente al unui plan oglindă. Astfel, dacă componenta de deplasare a unei astfel de operații este (0, 1, 2), atunci simbolul ei începe cu g(0, 1, 2), nu cu m(0, 1,2).

Tabele internaționale de cristalografie (1983). Vol. A, editat de TH. HAHN, în special §§ 1.1, 1.3, 1.4, 7 și 11. Dordrecht: Kluwer Academic Publishers.

International Tables for Crystallography (1989). Vol. A, ed. a 2-a, revizuită, editată de TH. HAHN. Dordrecht: Kluwer Academic Publishers.

WOLFF, P. M. DE, BELOV, N. V., BERTAUT, E. F., BUERGER, M. J., DONNAY, J. D. H., FISCHER, W., HAHN, TH., KOPTSIK, V. A., MACKAY, A. L., WONDRATSCHEK, H., WILSON, A. J. C. & ABRAHAMS, S. C. (1985). Acta Cryst. A41, 278-280.

WOLFF, P. M. DE, BILLIET, Y., DONNAY, J. D. H., FISCHER, W., GALIULIN, R. B., GLAZER, A. M., SENECHAL, M., SHOEMAKER, D. P., WONDRATSCHEK, H., HAHN, TH., WILSON, A. J. C. & ABRAHAMS, S. C. (1989). Acta Cryst. A45, 494-499.

…vectori. Simbolurile planurilor de alunecare c, n și k pentru cele trei diagrame (2), (9) și (14) din figura 3 au fost, desigur, atribuite în conformitate cu tabelul 3. Un membru al Comitetului ad-hoc (profesorul Wondratschek) consideră că simbolul n pentru diagrama (9) intră în conflict cu noțiunile tradiționale despre n planuri. El propune atribuirea unui simbol special pentru diagrama (9). Cu toate acestea, această propunere nu a primit un sprijin adecvat în cadrul Comitetului Ad-hoc.
.

Simboluri pentru elemente de simetrie și operații de simetrie