Men även om metoderna i det föregående avsnittet är användbara för att beskriva och visa provdata, visar sig statistikens verkliga styrka när vi använder prov för att ge oss information om populationer. I detta sammanhang är en population hela samlingen av objekt av intresse, till exempel försäljningspriserna för alla enfamiljshus på bostadsmarknaden som representeras av vårt dataset. Vi skulle vilja veta mer om denna population för att kunna fatta ett beslut om vilket hus vi ska köpa, men de enda data vi har är ett slumpmässigt urval av 30 försäljningspriser.

Nåväl kan vi använda ”statistiskt tänkande” för att dra slutsatser om populationen av intresse genom att analysera data från urvalet. I synnerhet använder vi begreppet modell – en matematisk abstraktion av den verkliga världen – som vi anpassar till provdata. Om denna modell ger en rimlig anpassning till uppgifterna, dvs. om den kan approximera det sätt på vilket uppgifterna varierar, antar vi att den också kan approximera populationens beteende. Modellen utgör då grunden för att fatta beslut om populationen, till exempel genom att identifiera mönster, förklara variationer och förutsäga framtida värden. Naturligtvis kan denna process bara fungera om provdata kan anses vara representativa för populationen.

Ibland, även när vi vet att ett prov inte har valts ut slumpmässigt, kan vi ändå modellera det. Då kan vi kanske inte formellt dra slutsatser om en population utifrån urvalet, men vi kan ändå modellera urvalets underliggande struktur. Ett exempel är ett bekvämlighetsurval – ett urval som valts ut mer av bekvämlighetsskäl än på grund av dess statistiska egenskaper. Vid modellering av sådana urval bör alla resultat rapporteras med en varning om att begränsa alla slutsatser till objekt som liknar dem som ingår i urvalet. En annan typ av exempel är när urvalet omfattar hela populationen. Vi skulle till exempel kunna modellera data för alla 50 delstater i USA för att bättre förstå eventuella mönster eller systematiska samband mellan delstaterna.

Då den verkliga världen kan vara extremt komplicerad (på det sätt som datavärden varierar eller interagerar med varandra) är modeller användbara eftersom de förenklar problem så att vi bättre kan förstå dem (och sedan fatta mer effektiva beslut). Å ena sidan behöver vi därför modeller som är tillräckligt enkla för att vi lätt ska kunna använda dem för att fatta beslut, men å andra sidan behöver vi modeller som är tillräckligt flexibla för att ge goda approximationer av komplexa situationer. Lyckligtvis har många statistiska modeller utvecklats under årens lopp som ger en effektiv balans mellan dessa två kriterier. En sådan modell, som ger en bra utgångspunkt för de mer komplicerade modeller vi överväger senare, är normalfördelningen.

Från ett statistiskt perspektiv är en sannolikhetsfördelning en teoretisk modell som beskriver hur en slumpvariabel varierar. För våra syften representerar en slumpvariabel de datavärden som är av intresse i populationen, till exempel försäljningspriserna för alla enfamiljshus på vår bostadsmarknad. Ett sätt att representera populationsfördelningen av datavärden är i ett histogram, som beskrivs i avsnitt 1.1. Skillnaden nu är att histogrammet visar hela populationen i stället för bara urvalet. Eftersom populationen är så mycket större än urvalet kan histogrammets bins (de på varandra följande intervall av data som utgör de horisontella intervallen för staplarna) vara mycket mindre, till exempel visar följande ett histogram för en simulerad population på 1 000 försäljningspriser.

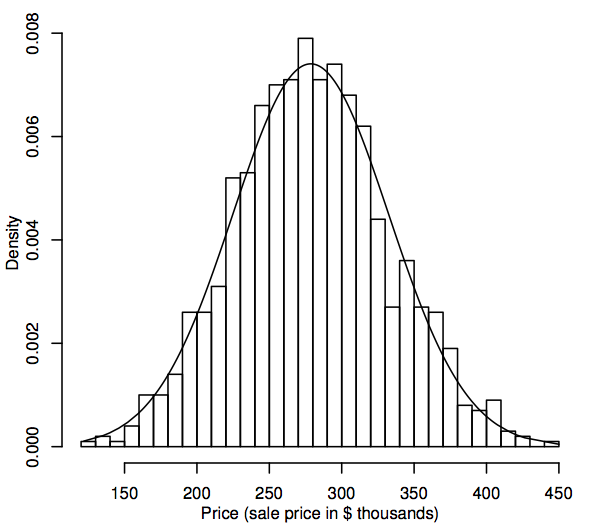
När populationen blir större kan vi föreställa oss att histogrammets staplar blir tunnare och fler, tills histogrammet liknar en jämn kurva i stället för en serie steg. Denna jämna kurva kallas densitetskurva och kan ses som den teoretiska versionen av befolkningshistogrammet. Densitetskurvor ger också ett sätt att visualisera sannolikhetsfördelningar som t.ex. normalfördelningen. En normal densitetskurva överlagras på histogrammet ovan. Det simulerade befolkningshistogrammet följer kurvan ganska nära, vilket tyder på att den här simulerade befolkningsfördelningen ligger ganska nära det normala.

För att se hur en teoretisk fördelning kan visa sig vara användbar för att göra statistiska slutsatser om populationer som den i vårt exempel med bostadspriser, måste vi titta närmare på normalfördelningen. Till att börja med betraktar vi en särskild version av normalfördelningen, standardnormalen, som representeras av följande densitetskurva.

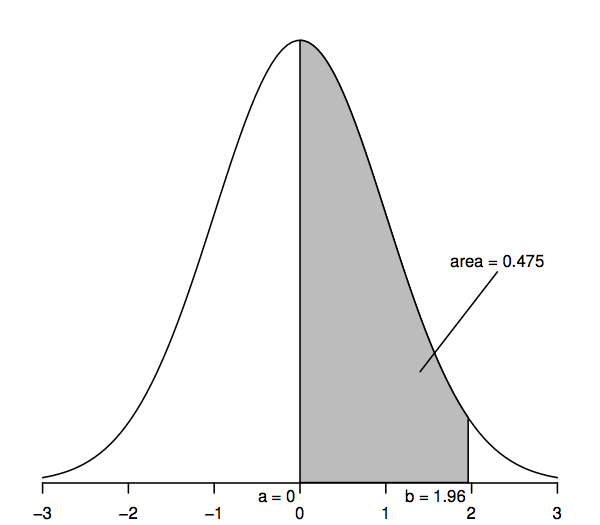
Summavariabler som följer en standardnormalfördelning har ett medelvärde på 0 (så att kurvan är symmetrisk kring 0, som ligger under kurvans högsta punkt) och en standardavvikelse på 1 (så att kurvan har en böjningspunkt – där kurvan böjer sig först åt ena hållet och sedan åt det andra – vid +1 och -1). Den normala densitetskurvan kallas ibland för ”klockkurvan” eftersom dess form liknar en klockas.

Den viktigaste egenskapen hos den normala densitetskurvan som gör det möjligt för oss att göra statistiska slutsatser är att områdena under kurvan representerar sannolikheter. Hela arean under kurvan är ett, medan arean under kurvan mellan en punkt på den horisontella axeln (till exempel a) och en annan punkt (till exempel b) representerar sannolikheten för att en slumpvariabel som följer en standardnormalfördelning ligger mellan a och b. Så till exempel visar figuren ovan att sannolikheten är 0.475 att en standardnormal slumpvariabel ligger mellan a=0 och b=1,96, eftersom arean under kurvan mellan a=0 och b=1,96 är 0,475.

Vi kan få fram värden för dessa areor eller sannolikheter från en mängd olika källor: siffertabeller, miniräknare, kalkylatorer, kalkylprogram eller statistiska programvaror, webbplatser och så vidare. Nedan skriver vi bara ut några utvalda värden eftersom de flesta av de senare beräkningarna använder en generalisering av normalfördelningen som kallas ”t-fördelning”. I stället för områden som det som är skuggat i figuren ovan kommer det också att bli mer användbart att betrakta ”svansområden” (t.ex, till höger om punkt b), och för att det ska vara förenligt med senare tabeller med tal, gör följande tabell det möjligt att beräkna sådana svansområden:

I synnerhet är det övre svansområdet till höger om 1,96 0,025; detta är likvärdigt med att säga att området mellan 0 och 1,96 är 0,475 (eftersom hela området under kurvan är 1 och området till höger om 0 är 0,5). På samma sätt är området med två svansar, som är summan av områdena till höger om 1,96 och till vänster om -1,96, två gånger 0,025 eller 0,05.

Hur hjälper allt detta oss att göra statistiska slutsatser om populationer som den i vårt exempel med bostadspriser? Den grundläggande idén är att vi anpassar en normalfördelningsmodell till våra provdata och sedan använder denna modell för att dra slutsatser om motsvarande population. Vi kan till exempel använda sannolikhetsberäkningar för en normalfördelning (som visas i figuren ovan) för att göra sannolikhetsuttalanden om en population som modellerats med hjälp av den normalfördelningen – vi kommer att visa exakt hur man gör detta i avsnitt 1.3. Innan vi gör det stannar vi dock upp för att överväga en aspekt av denna slutledningssekvens som kan vara avgörande eller brytande för processen. Ger modellen en tillräckligt nära approximation av mönstret för provvärdena så att vi kan vara säkra på att modellen på ett adekvat sätt representerar populationsvärdena? Ju bättre approximation, desto mer tillförlitliga blir våra slutsatser.

Vi såg tidigare hur en täthetskurva kan betraktas som ett histogram med en mycket stor urvalsstorlek. Så ett sätt att bedöma om vår population följer en normalfördelningsmodell är att konstruera ett histogram från våra provdata och visuellt avgöra om det ”ser normalt ut”, det vill säga ungefär symmetriskt och klockformat. Detta är ett något subjektivt beslut, men med erfarenhet bör du märka att det blir lättare att urskilja tydligt icke-normala histogram från de som är någorlunda normala. Medan histogrammet ovan till exempel tydligt ser ut som en normal täthetskurva, är normaliteten hos histogrammet med 30 exempelförsäljningspriser i avsnitt 1.1 mindre säker. En rimlig slutsats i detta fall skulle vara att även om detta provhistogram inte är perfekt symmetriskt och klockformat är det tillräckligt nära att motsvarande (hypotetiska) populationshistogram mycket väl skulle kunna vara normalt.

Ett alternativt sätt att bedöma normaliteten är att konstruera en QQ-plot (quantile-quantile plot), även känd som en normal sannolikhetsplot, som visas här för husprisdata:

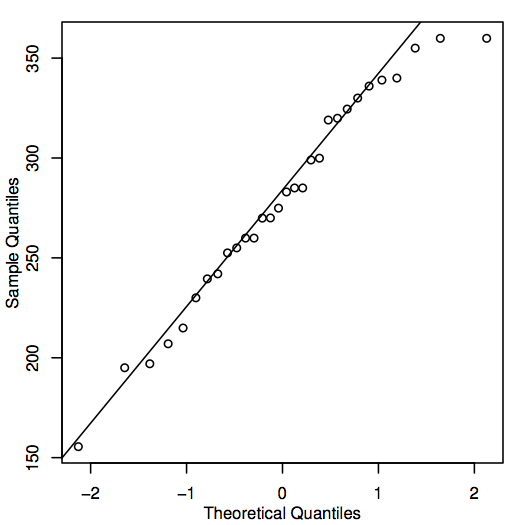
Om punkterna i QQ-plot ligger nära den diagonala linjen kan motsvarande populationsvärden mycket väl vara normala. Om punkterna i allmänhet ligger långt från linjen kan normaliteten ifrågasättas. Återigen är detta ett något subjektivt beslut som blir lättare att fatta med erfarenhet. I det här fallet, med tanke på det ganska lilla urvalet, ligger punkterna troligen tillräckligt nära linjen för att det är rimligt att dra slutsatsen att populationsvärdena kan vara normala.

Det finns också en rad olika kvantitativa metoder för att bedöma normalitet – se avsnitt 6.3.