Definition
Ett polynom i variabeln x är en funktion som kan skrivas i formen,
där an, an-1 , …, a2, a1, a0 är konstanter. Vi kallar den term som innehåller den högsta potensen av x (dvs. anxn) för den ledande termen, och vi kallar an för den ledande koefficienten. Graden av polynomet är potensen av x i den ledande termen. Vi har redan sett polynomier av grad 0, 1 och 2 som var konstanta, linjära respektive kvadratiska funktioner. Polynom av graderna 3, 4 och 5 har också särskilda namn: kubiska, kvartiska och kvintliga funktioner. Polynomier med grad n > 5 kallas helt enkelt för n:e gradens polynomier. Namnen på olika polynomfunktioner sammanfattas i tabellen nedan.
| Polynomets grad | Funktionens namn |
| 0 | Konstant funktion. |
| 1 | Linjär funktion |
| 2 | Kvadratisk funktion |
| 3 | Kubisk funktion |
| 4 | Quartisk funktion |
| 5 | Quintisk funktion |
| n (där n > 5) | polynom av n:e graden |
Vissa exempel på polynom är:
Polynomers begränsande beteende
En funktions begränsande beteende beskriver vad som händer med funktionen när x → ±∞. Graden av ett polynom och tecknet på dess ledande koefficient dikterar dess begränsningsbeteende. I synnerhet
Dessa resultat sammanfattas i tabellen nedan.
Du kan använda denna information för att avgöra om ett polynom har udda eller jämn grad och om den ledande koefficienten är positiv eller negativ, helt enkelt genom att inspektera dess graf.
Följande grafer för polynom visar varje beteende som beskrivs i tabellen ovan.
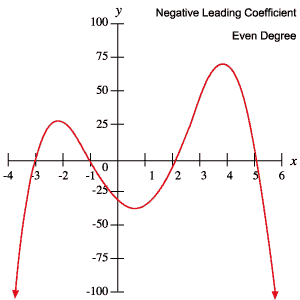
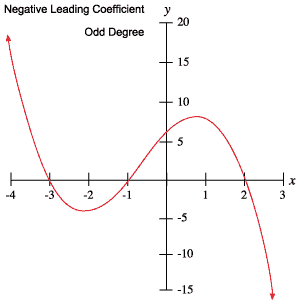
Rötter och vändpunkter
Graden på ett polynom säger ännu mer om det än det begränsande beteendet. Närmare bestämt kan ett polynom av n:e graden ha högst n verkliga rötter (x-intercepts eller nollor) om man räknar multiplikatorerna. Anta till exempel att vi tittar på ett 6:e gradens polynom som har 4 distinkta rötter. Om två av de fyra rötterna har multiplicitet 2 och de andra två har multiplicitet 1, vet vi att det inte finns några andra rötter eftersom vi har räknat med alla 6 rötterna. Detta beror på att rötter med en multiplicitet på två (även kända som dubbla rötter) räknas som två rötter.
Var medveten om att ett n:e gradens polynom inte behöver ha n reella rötter – det kan ha färre eftersom det har imaginära rötter. Observera att ett polynom av udda grad måste ha minst en reell rot eftersom funktionen närmar sig – ∞ i ena änden och + ∞ i den andra; en kontinuerlig funktion som växlar från negativ till positiv måste skära x-axeln någonstans däremellan. Dessutom kan ett n:e gradens polynom ha högst n – 1 vändpunkter. En vändpunkt är en punkt där funktionen övergår från ökande till minskande eller från minskande till ökande, vilket framgår av figuren nedan. Återigen behöver ett n:e gradens polynom inte ha n – 1 vändpunkter, det kan ha färre.
Varning
Det är viktigt att inse skillnaden mellan jämna och udda funktioner och jämna och udda polynom. Varje funktion, f(x), är antingen jämn om,
f(-x) = x,
för alla x i området för f(x), eller udda om,
f(-x) = -x,
för alla x i området för f(x), eller varken jämn eller udda om ingen av ovanstående är sanna påståenden.
Ett polynom av k:e graden, p(x), sägs ha jämn grad om k är ett jämnt tal och udda grad om k är ett udda tal. Kom ihåg att även om p(x) har jämn grad är det inte nödvändigtvis en jämn funktion. På samma sätt, om p(x) har udda grad, är den inte nödvändigtvis en udda funktion.
Vi använder också termerna jämn och udda för att beskriva rötter till polynom. Närmare bestämt har ett polynom p(x) rot x = a med multiplicitet k (dvs. x = a är en rot som upprepas k gånger) om (x – a)k är en faktor av p(x). Vi säger att x = a har jämn multiplicitet om k är ett jämnt tal och udda multiplicitet om k är ett udda tal.
Domän och område
Alla polynom har samma domän som består av alla reella tal. Området för polynom av udda grad består också av alla reella tal. Området för polynom av jämn grad är lite mer komplicerat och vi kan inte uttryckligen ange området för alla polynom av jämn grad. Om den ledande koefficienten är positiv sträcker sig funktionen till + ∞, medan den sträcker sig till – ∞ om den ledande koefficienten är negativ. Detta innebär att polynomier av jämn grad med positiv ledande koefficient har ett område där ymax betecknar det globala maximum som funktionen uppnår. I allmänhet är det inte möjligt att analytiskt bestämma polynomers maxima eller minima.
*****
I nästa avsnitt lär du dig polynomdivision, en teknik som används för att hitta rötterna till polynomfunktioner.
Polynomdivision