Introduktion

Föreställ dig det här – du har fått i uppdrag att prognostisera priset på nästa iPhone och har fått tillgång till historiska data. Detta inkluderar funktioner som kvartalsförsäljning, utgifter från månad till månad och en hel del saker som kommer med Apples balansräkning. Vilken typ av problem skulle du som datavetare klassificera detta som? Tidsseriemodellering, förstås.

Från att förutsäga försäljningen av en produkt till att uppskatta hushållens elförbrukning, är tidsserieprognoser en av de kärnkunskaper som alla datavetare förväntas känna till, om inte behärska. Det finns en uppsjö av olika tekniker där ute som du kan använda, och vi kommer att täcka en av de mest effektiva, kallad Auto ARIMA, i den här artikeln.

Vi kommer först att förstå begreppet ARIMA vilket kommer att leda oss till vårt huvudämne – Auto ARIMA. För att befästa våra begrepp kommer vi att ta upp ett dataset och implementera det i både Python och R.

Innehållsförteckning

1. Vad är en tidsserie?
2. Metoder för prognostisering av tidsserier
3. Introduktion till ARIMA
4. Steg för ARIMA-implementering
5. Varför behöver vi AutoARIMA?
6. Auto ARIMA-implementering (på datasetet för flygpassagerare)
7. Hur väljer Auto ARIMA parametrar?

Om du är bekant med tidsserier och dess tekniker (t.ex. glidande medelvärde, exponentiell utjämning och ARIMA), kan du hoppa direkt till avsnitt 4. Nybörjare kan börja med nedanstående avsnitt som är en kort introduktion till tidsserier och olika prognosmetoder.

Vad är en tidsserie?

Innan vi lär oss om tekniker för att arbeta med tidsseriedata måste vi först förstå vad en tidsserie faktiskt är och hur den skiljer sig från alla andra typer av data. Här är den formella definitionen av tidsserier – Det är en serie datapunkter som mäts med konsekventa tidsintervall. Detta innebär helt enkelt att vissa värden registreras med ett konstant intervall som kan vara timvis, dagligen, veckovis, var tionde dag och så vidare. Det som skiljer tidsserier från varandra är att varje datapunkt i serien är beroende av de föregående datapunkterna. Låt oss förstå skillnaden tydligare genom att ta ett par exempel.

Exempel 1:

Antag att du har ett dataset med personer som har tagit ett lån från ett visst företag (som visas i tabellen nedan). Tror du att varje rad kommer att vara relaterad till de föregående raderna? Absolut inte! Det lån som en person tar kommer att baseras på hans ekonomiska villkor och behov (det kan finnas andra faktorer som familjestorlek etc., men för enkelhetens skull tar vi bara hänsyn till inkomst och lånetyp) . Uppgifterna samlades inte heller in vid något specifikt tidsintervall. Det beror på när företaget fick en förfrågan om lånet.

Exempel 2:

Låt oss ta ett annat exempel. Anta att du har ett dataset som innehåller nivån av koldioxid i luften per dag (skärmdump nedan). Kommer du att kunna förutsäga den ungefärliga mängden koldioxid för nästa dag genom att titta på värdena från de senaste dagarna? Ja, naturligtvis. Om du observerar har data registrerats dagligen, det vill säga tidsintervallet är konstant (24 timmar).

Du måste ha fått en intuition om detta vid det här laget – det första fallet är ett enkelt regressionsproblem och det andra är ett tidsserieproblem. Tidsseriepusslet här kan visserligen också lösas med hjälp av linjär regression, men det är egentligen inte det bästa tillvägagångssättet eftersom det försummar värdens förhållande till alla relativa tidigare värden. Låt oss nu titta på några av de vanligaste teknikerna som används för att lösa tidsserieproblem.

Metoder för tidsserieprognoser

Det finns ett antal metoder för tidsserieprognoser och vi kommer kortfattat att behandla dem i detta avsnitt. Den detaljerade förklaringen och pythonkoderna för alla nedan nämnda tekniker finns i den här artikeln: 7 tekniker för tidsserieprognoser (med pythonkoder).

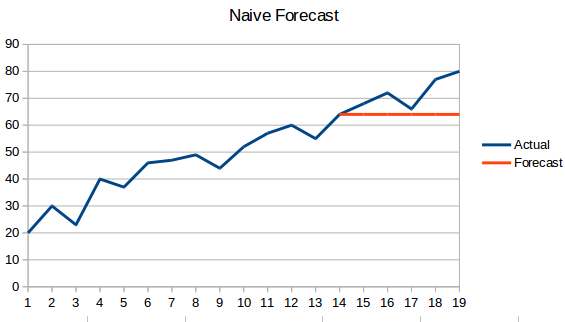
1. Naiv metod: I denna prognosteknik förutspås värdet av den nya datapunkten vara lika med den tidigare datapunkten. Resultatet skulle bli en platt linje, eftersom alla nya värden tar de tidigare värdena.
2. Simple Average: Nästa värde tas som ett genomsnitt av alla tidigare värden. Prognoserna här är bättre än ”Naive Approach” eftersom det inte resulterar i en platt linje, men här tas alla tidigare värden i beaktande, vilket kanske inte alltid är användbart. När du till exempel ska förutsäga dagens temperatur skulle du ta hänsyn till de senaste sju dagarnas temperatur snarare än temperaturen för en månad sedan.
3. Glidande medelvärde : Detta är en förbättring jämfört med den tidigare tekniken. Istället för att ta genomsnittet av alla tidigare punkter tas genomsnittet av ”n” tidigare punkter som det förutspådda värdet.
4. Viktat glidande medelvärde : Ett viktat glidande medelvärde är ett glidande medelvärde där de tidigare ”n” värdena ges olika vikt.
5. Enkel exponentiell utjämning: I den här tekniken tilldelas större vikter till nyare observationer än till observationer från ett avlägset förflutet.
6. Holts linjära trendmodell: Denna metod tar hänsyn till trenden i datasetet. Med trend menas seriens ökande eller minskande karaktär. Antag att antalet bokningar på ett hotell ökar varje år, då kan vi säga att antalet bokningar visar en ökande trend. Prognosfunktionen i denna metod är en funktion av nivå och trend.
7. Holt Winters metod: Denna algoritm tar hänsyn till både trenden och säsongsvariationen i serien. Till exempel – antalet bokningar på ett hotell är högt på helgerna & lågt på vardagarna och ökar varje år; det finns en veckosäsonglighet och en ökande trend.
8. ARIMA: ARIMA är en mycket populär teknik för tidsseriemodellering. Den beskriver korrelationen mellan datapunkter och tar hänsyn till skillnaden mellan värdena. En förbättring av ARIMA är SARIMA (eller säsongsbaserad ARIMA). Vi kommer att titta på ARIMA lite mer i detalj i följande avsnitt.

Introduktion till ARIMA

I det här avsnittet kommer vi att göra en snabb introduktion till ARIMA som kommer att vara till hjälp för att förstå Auto Arima. En detaljerad förklaring av Arima, parametrar (p,q,d), diagram (ACF PACF) och implementering ingår i den här artikeln : Fullständig handledning i tidsserier.

ARIMA är en mycket populär statistisk metod för prognostisering av tidsserier. ARIMA står för Auto-Regressive Integrated Moving Averages. ARIMA-modeller fungerar utifrån följande antaganden –

• Dataserien är stationär, vilket innebär att medelvärdet och variansen inte ska variera med tiden. En serie kan göras stationär med hjälp av logtransformation eller genom att differentiera serien.
• Data som tillhandahålls som indata måste vara en univariat serie, eftersom arima använder de tidigare värdena för att förutsäga de framtida värdena.

ARIMA har tre komponenter – AR (autoregressiv term), I (differentieringsterm) och MA (glidande medelvärde term). Låt oss förstå var och en av dessa komponenter –

• AR-termen avser de tidigare värden som används för att förutsäga nästa värde. AR-termen definieras av parametern ”p” i arima. Värdet på ”p” bestäms med hjälp av PACF-plotten.
• MA-termen används för att definiera antalet tidigare prognosfel som används för att förutsäga de framtida värdena. Parametern ”q” i arima representerar MA-termen. ACF-plotten används för att identifiera det korrekta ”q”-värdet.
• Differentieringsordning anger hur många gånger differentieringsoperationen utförs på serien för att göra den stationär. Test som ADF och KPSS kan användas för att avgöra om serien är stationär och hjälper till att identifiera d-värdet.

Steg för ARIMA-implementering

De allmänna stegen för att implementera en ARIMA-modell är –

1. Ladda data: Det första steget för modellbygge är naturligtvis att ladda datamängden
2. Förbehandling: Beroende på datasetet kommer stegen för förbearbetning att definieras. Detta kommer att innefatta att skapa tidsstämplar, konvertera dtypen för datum/tidskolumnen, göra serierna univariata osv.
3. Gör serierna stationära: För att uppfylla antagandet är det nödvändigt att göra serien stationär. Detta skulle innefatta att kontrollera seriens stationaritet och utföra nödvändiga transformationer
4. Bestäm d-värdet: För att göra serien stationär kommer antalet gånger som differensoperationen utfördes att tas som d-värde
5. Skapa ACF- och PACF-plottar: Detta är det viktigaste steget i ARIMA-implementeringen. ACF PACF-plottar används för att bestämma ingångsparametrarna för vår ARIMA-modell
6. Bestäm p- och q-värdena: Läs av värdena för p och q från diagrammen i föregående steg
7. Anpassa ARIMA-modellen: Med hjälp av de bearbetade data och parametervärden som vi beräknade i föregående steg, anpassa ARIMA-modellen
8. Förutsäg värden på valideringsuppsättningen: Beräkna RMSE: För att kontrollera modellens prestanda, kontrollera RMSE-värdet med hjälp av förutsägelserna och de faktiska värdena på valideringsuppsättningen

Varför behöver vi Auto ARIMA?

Och även om ARIMA är en mycket kraftfull modell för prognostisering av tidsseriedata, så slutar processerna för dataförberedelse och parameterinställning med att vara riktigt tidskrävande. Innan du implementerar ARIMA måste du göra serien stationär och bestämma värdena för p och q med hjälp av de diagram som vi diskuterade ovan. Auto ARIMA gör den här uppgiften riktigt enkel för oss eftersom den eliminerar steg 3 till 6 som vi såg i föregående avsnitt. Nedan följer de steg du bör följa för att implementera auto ARIMA:

1. Lad in data: Det här steget kommer att vara detsamma. Ladda in data i din anteckningsbok
2. Förbehandling av data: Inmatningen ska vara univariat, släpp därför de andra kolumnerna
3. Fit Auto ARIMA: Anpassa modellen på de univariata serierna
4. Förutsäga värden på valideringsuppsättningen: Beräkna RMSE: Kontrollera modellens prestanda med hjälp av de förutspådda värdena mot de faktiska värdena

Vi har helt förbigått valet av p- och q-funktionen som du kan se. Vilken lättnad! I nästa avsnitt kommer vi att implementera auto ARIMA med hjälp av ett leksaksdataset.

Implementering i Python och R

Vi kommer att använda datasetetet International-Air-Passenger. Detta dataset innehåller månatliga totaler av antalet passagerare (i tusen). Det har två kolumner – månad och antal passagerare. Du kan ladda ner datasetet från den här länken.

#load the datadata = pd.read_csv('international-airline-passengers.csv')#divide into train and validation settrain = datavalid = data#preprocessing (since arima takes univariate series as input)train.drop('Month',axis=1,inplace=True)valid.drop('Month',axis=1,inplace=True)#plotting the datatrain.plot()valid.plot()

#building the modelfrom pyramid.arima import auto_arimamodel = auto_arima(train, trace=True, error_action='ignore', suppress_warnings=True)model.fit(train)forecast = model.predict(n_periods=len(valid))forecast = pd.DataFrame(forecast,index = valid.index,columns=)#plot the predictions for validation setplt.plot(train, label='Train')plt.plot(valid, label='Valid')plt.plot(forecast, label='Prediction')plt.show()

#calculate rmsefrom math import sqrtfrom sklearn.metrics import mean_squared_errorrms = sqrt(mean_squared_error(valid,forecast))print(rms)

output -76.51355764316357

Nedan följer R-koden för samma problem:

# loading packageslibrary(forecast)library(Metrics)# reading datadata = read.csv("international-airline-passengers.csv")# splitting data into train and valid setstrain = datavalid = data# removing "Month" columntrain$Month = NULL# training modelmodel = auto.arima(train)# model summarysummary(model)# forecastingforecast = predict(model,44)# evaluationrmse(valid$International.airline.passengers, forecast$pred)

Hur väljer Auto Arima de bästa parametrarna

I ovanstående kod använde vi helt enkelt .fit() kommandot för att anpassa modellen utan att behöva välja kombinationen av p, q, d. Men hur räknade modellen ut den bästa kombinationen av dessa parametrar? Auto ARIMA tar hänsyn till de AIC- och BIC-värden som genereras (som du kan se i koden) för att bestämma den bästa kombinationen av parametrar. AIC- (Akaike Information Criterion) och BIC- (Bayesian Information Criterion) värden är estimatorer för att jämföra modeller. Ju lägre dessa värden är, desto bättre är modellen.

Kontrollera dessa länkar om du är intresserad av matematiken bakom AIC och BIC.

Slutanteckningar och vidare läsning

Jag har funnit att auto ARIMA är den enklaste tekniken för att utföra tidsserieprognoser. Att känna till en genväg är bra, men det är också viktigt att känna till matematiken bakom den. I den här artikeln har jag skummat igenom detaljerna om hur ARIMA fungerar men se till att du går igenom de länkar som finns i artikeln. För att du enkelt ska kunna hitta dem, här är länkarna igen:

• En omfattande guide för nybörjare till tidsserieprognoser i Python
• En fullständig handledning till tidsserier i R
• 7 tekniker för tidsserieprognoser (med pythonkoder)

Jag föreslår att du praktiserar det som vi lärt oss här på det här övningsproblemet: Övningsproblem för tidsserier. Du kan också ta vår utbildningskurs som skapats på samma övningsproblem, Time series forecasting, för att ge dig ett försprång.