I den här artikeln kommer jag att förklara hur 2D-konvolutioner implementeras som matrismultiplikationer. Den här förklaringen är baserad på anteckningarna från CS231n Convolutional Neural Networks for Visual Recognition (Module 2). Jag antar att läsaren är bekant med begreppet konvolutionsoperation i samband med ett djupt neuralt nätverk. Om inte har denna repo en rapport och utmärkta animationer som förklarar vad konvolutioner är. Koden för att reproducera beräkningarna i den här artikeln kan laddas ner här.
Litet exempel
Antag att vi har en 4 x 4 bild med en enda kanal, X, och att dess pixelvärden är följande:

Antag vidare att vi definierar en 2D-falsning med följande egenskaper:

Detta innebär att det kommer att finnas 9 2 x 2 bildfläckar som kommer att multipliceras elementvis med matrisen W, så här:

Dessa bildfläckar kan representeras som 4-dimensionella kolumnvektorer och sammanfogas för att bilda en enda 4 x 9-matris, P, på följande sätt:

Bemärk att den i:e kolumnen i matrisen P i själva verket är den i:e bildfläckens kolonnvektorform.
Matrisen av vikter för konvolutionslagret, W, kan plattas till en 4-dimensionell radvektor , K, på följande sätt:
För att utföra konvolutionen matrismultiplicerar vi först K med P för att få en 9-dimensionell rakvektor (1 x 9-matris) vilket ger oss:
Därefter omformar vi resultatet av K P till den korrekta formen, som är en 3 x 3 x 1 matris (kanaldimensionen sist). Kanaldimensionen är 1 eftersom vi ställer in utgångsfiltren till 1. Höjden och bredden är 3 eftersom enligt anteckningarna till CS231n:

Detta innebär att resultatet av konvolutionen är:
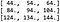
Vad som kontrolleras om vi utför konvolutionen med hjälp av PyTorchs inbyggda funktioner (se den här artiklarnas medföljande kod för detaljer).
Större exempel
Exemplet i det föregående avsnittet utgår från en enda bild och utgångskanalerna för konvolutionen är 1. Vad skulle förändras om vi lättade på dessa antaganden?
Låt oss anta att vår indata till konvolutionen är en 4 x 4 bild med 3 kanaler med följande pixelvärden:

Vad gäller vår konvolution kommer vi att ställa in den så att den har samma egenskaper som i det föregående avsnittet, förutom att dess utgående filter är 2. Detta innebär att den initiala viktmatrisen, W, måste ha formen (2, 2, 2, 2, 3) dvs. (utgångsfilter, kärnans höjd, kärnans bredd, ingångsbildens kanaler). Låt oss ställa in W på följande värden:

Bemärk att varje utgångsfilter kommer att ha sin egen kärna (vilket är anledningen till att vi har 2 kärnor i det här exemplet) och att varje kärnas kanal är 3 (eftersom inmatningsbilden har 3 kanaler).
Då vi fortfarande konvolverar en 2 x 2 kärna på en 4 x 4 bild med 0 zero-padding och stride 1, är antalet bildfläckar fortfarande 9. Matrisen för bildfläckarna, P, kommer dock att vara annorlunda. Närmare bestämt kommer den i:e kolumnen i P att vara sammanfogningen av värdena för den första, andra och tredje kanalen (som en kolumnvektor) som motsvarar bildfältet i. P kommer nu att vara en matris på 12 x 9. Raderna är 12 eftersom varje bildflik har 3 kanaler och varje kanal har 4 element eftersom vi har satt kärnstorleken till 2 x 2. Så här ser P ut:

Som för W kommer varje kärna att plattas till en radvektor och sammanfogas radsvis för att bilda en 2 x 12 matris, K. Den i:e raden i K är sammanlänkningen av de första, andra och tredje kanalvärdena (i radvektorform) som motsvarar den i:e kärnan. Så här kommer K att se ut:

Nu återstår bara att utföra matrismultiplikationen K P och omforma den till rätt form. Den korrekta formen är en 3 x 3 x 2-matris (kanaldimensionen sist). Här är resultatet av multiplikationen:

Och här är resultatet efter att ha omformat den till en 3 x 3 x 2-matris:

Vad som återigen kontrolleras om vi utför konvolutionen med hjälp av PyTorchs inbyggda funktioner (se den här artikelns medföljande kod för detaljer).
So What?
Varför ska vi bry oss om att uttrycka 2D-faltningar i termer av matrismultiplikationer? Förutom att vi har en effektiv implementering som lämpar sig för att köras på en GPU, kommer kunskapen om detta tillvägagångssätt att göra det möjligt för oss att resonera om beteendet hos ett djupt konvolutionellt neuralt nätverk. Till exempel har He et. al. (2015) uttryckt 2D-falsningar i termer av matrismultiplikationer vilket gjorde att de kunde tillämpa egenskaperna hos slumpmässiga matriser/vektorer för att argumentera för en bättre initialiseringsrutin för vikter.
Slutsats
I den här artikeln har jag förklarat hur man utför 2D-falsningar med hjälp av matrismultiplikationer genom att gå igenom två små exempel. Jag hoppas att detta är tillräckligt för att du ska kunna generalisera till godtyckliga inmatningsbildsdimensioner och convolutionsegenskaper. Låt mig veta i kommentarerna om något är oklart.
1D-konvolution
Metoden som beskrivs i den här artikeln generaliseras även till 1D-konvolutioner.
Antag till exempel att din indata är en 3-kanalig 12-dimensionell vektor på följande sätt:

Om vi ställer in vår 1D-konvolution så att den har följande parametrar:
- kärnstorlek: 1 x 4
- utgångskanaler: 2
- stride: 2
- padding: 0
- bias: 0
Då blir parametrarna i konvolutionen, W, en tensor med formen (2 , 3, 1, 4). Låt oss ställa in W på följande värden:

Baserat på parametrarna för konvolutionen kommer matrisen av ”bild”-fläckar P att ha formen (12, 5) (5 bildfläckar där varje bildfläck är en 12-D-vektor eftersom en fläck har 4 element över 3 kanaler) och kommer att se ut så här:

Nästan plattar vi till W för att få fram K, som har formen (2, 12) eftersom det finns 2 kärnor och varje kärna har 12 element. Så här ser K ut:
Nu kan vi multiplicera K med P vilket ger:
Slutligt omformar vi K P till rätt form, som enligt formeln är en ”bild” med formen (1, 5). Detta innebär att resultatet av denna konvolution är en tensor med formen (2, 1, 5) eftersom vi har ställt in utgångskanalerna på 2. Så här ser slutresultatet ut:

Vad som förväntat kontrolleras om vi skulle utföra konvolutionen med hjälp av PyTorchs inbyggda funktioner.