Bayesianska trovärdighetsnätverk eller Bayesianska nätverk eller trovärdighetsnätverk är en probabilistisk grafisk modell (PGM) som representerar villkorliga beroenden mellan slumpmässiga variabler genom en riktad acyklisk graf (DAG).
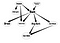
I dag kommer jag att försöka förklara de viktigaste aspekterna av Belief Networks, särskilt för tillämpningar som kan vara relaterade till Social Network Analysis (SNA). Dessutom kommer jag att visa ett exempel på en implementering av denna typ av nätverk.
Vad använder vi Bayesianska nätverk till?
Bayesianska nätverk används inom många områden. Till exempel sjukdomsdiagnoser, optimerad webbsökning, skräppostfiltrering, genreglerande nätverk osv. Och denna lista kan förlängas. Huvudsyftet med dessa nätverk är att försöka förstå strukturen hos kausalitetsrelationerna. För att förtydliga detta, låt oss betrakta ett problem med sjukdomsdiagnostik. Med givna symtom och deras resulterande sjukdom konstruerar vi vårt trovärdighetsnätverk och när en ny patient kommer kan vi dra slutsatser om vilken eller vilka sjukdomar den nya patienten kan ha genom att ange sannolikheter för varje sjukdom. På samma sätt kan dessa kausalitetsrelationer konstrueras för andra problem och inferenstekniker kan tillämpas för att uppnå intressanta resultat.
Snabb sannolikhetsgenomgång
För att fräscha upp våra minnen vill jag först ge er en definition av villkorlig egenskap. Villkorlig sannolikhet är sannolikheten för en slumpvariabel när någon annan slumpvariabel är given. Den visas genom
Om dessa två slumpvariabler är beroende,
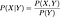
Om de är oberoende, då
Matematisk definition av trovärdighetsnätverk
Sannolikheterna beräknas i trosnätverken med följande formel
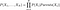
Som du förstår av formeln, för att kunna beräkna den gemensamma fördelningen måste vi ha villkorliga sannolikheter som anges av nätverket. Men om vi dessutom har den gemensamma fördelningen kan vi börja ställa intressanta frågor. I det första exemplet frågar vi till exempel efter sannolikheten för ”REGN” om ”SEASON” är ”WINTER” och ”DOG BARK” är ”TRUE”.
Python Exempel på Belief Network
Så, jag tror att detta räcker med teori och låt oss se några riktiga exempel med mitt nuvarande favoritprogrammeringsspråk Python ❤️ Innan du fortsätter kan du hitta Jupyter Notebook som jag har skrivit här.
# create the nodes
season = BbnNode(Variable(0, 'season', ), )
atmos_pres = BbnNode(Variable(1, 'atmos_press', ), )
allergies = BbnNode(Variable(2, 'allergies', ), )
rain = BbnNode(Variable(3, 'rain', ), )
grass = BbnNode(Variable(4, 'grass', ), )
umbrellas = BbnNode(Variable(5, 'umbrellas', ), )
dog_bark = BbnNode(Variable(6, 'dog_bark', ), )
cat_mood = BbnNode(Variable(7, 'cat_mood', ), )
cat_hide = BbnNode(Variable(8, 'cat_hide', ), )bbn = Bbn() \
.add_node(season) \
.add_node(atmos_pres) \
.add_node(allergies) \
.add_node(rain) \
.add_node(grass) \
.add_node(umbrellas) \
.add_node(dog_bark) \
.add_node(cat_mood) \
.add_node(cat_hide) \
.add_edge(Edge(season, allergies, EdgeType.DIRECTED)) \
.add_edge(Edge(season, umbrellas, EdgeType.DIRECTED)) \
.add_edge(Edge(season, rain, EdgeType.DIRECTED)) \
.add_edge(Edge(atmos_pres, rain, EdgeType.DIRECTED)) \
.add_edge(Edge(rain, grass, EdgeType.DIRECTED)) \
.add_edge(Edge(rain, umbrellas, EdgeType.DIRECTED)) \
.add_edge(Edge(rain, dog_bark, EdgeType.DIRECTED)) \
.add_edge(Edge(rain, cat_mood, EdgeType.DIRECTED)) \
.add_edge(Edge(dog_bark, cat_hide, EdgeType.DIRECTED)) \
.add_edge(Edge(cat_mood, cat_hide, EdgeType.DIRECTED))
Vi beskrev först våra noder med betingade sannolikheter. Du bör märka att jag hoppade över några möjliga tillståndsvärden för enkelhetens skull. Till exempel kan säsongsvariabeln ta andra värden ”vår” och ”höst”. Så idén är densamma.
Nej, låt oss kontrollera om vårt nätverk är korrekt konstruerat eller inte.
with warnings.catch_warnings():
warnings.simplefilter('ignore')
graph = convert_for_drawing(bbn)
pos = nx.nx_agraph.graphviz_layout(graph, prog='neato')plt.figure(figsize=(20, 10))
plt.subplot(121)
labels = dict()
nx.draw(graph, pos=pos, with_labels=True, labels=labels)
plt.title('BBN DAG')
Detta kodutdrag skulle resultera i följande graf
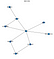
Så, du kan se att det här nätverket stämmer överens med min fantasifulla ritning i början. Låt oss nu göra några inferenser på detta trosnätverk.
# convert the BBN to a join tree
join_tree = InferenceController.apply(bbn)# insert an observation evidence
ev = EvidenceBuilder() \
.with_node(join_tree.get_bbn_node_by_name('season')) \
.with_evidence('winter', 1.0) \
.build()join_tree.set_observation(ev)# print the marginal probabilities
for node in join_tree.get_bbn_nodes():
potential = join_tree.get_bbn_potential(node)
print(node)
print(potential)
print('--------------------->')
Detta kodutdrag ger i princip bevis för nätverket som är att säsongen är vinter med en sannolikhet på 1,0. Enligt detta bevis får vi följande resultat när vi gör inferensen.
0|season|winter,summer
0=winter|1.00000
0=summer|0.00000
--------------------->
2|allergies|allergic,non_alergic
2=allergic|0.70000
2=non_alergic|0.30000
--------------------->
3|rain|rainy,sunny
3=rainy|0.80000
3=sunny|0.20000
--------------------->
4|grass|grass,no_grass
4=grass|0.70000
4=no_grass|0.30000
--------------------->
1|atmos_press|high,low
1=high|0.50000
1=low|0.50000
--------------------->
5|umbrellas|on,off
5=on|0.95200
5=off|0.04800
--------------------->
6|dog_bark|bark,not_bark
6=bark|0.66000
6=not_bark|0.34000
--------------------->
7|cat_mood|good,bad
7=good|0.23000
7=bad|0.77000
--------------------->
8|cat_hide|hide,show
8=hide|0.87150
8=show|0.12850
--------------------->
När vi lägger till ytterligare bevis, t.ex. att hunden inte skäller
# convert the BBN to a join tree
join_tree = InferenceController.apply(bbn)# insert an observation evidence
ev = EvidenceBuilder() \
.with_node(join_tree.get_bbn_node_by_name('season')) \
.with_evidence('winter', 1.0) \
.build()ev2 = EvidenceBuilder() \
.with_node(join_tree.get_bbn_node_by_name('dog_bark')) \
.with_evidence('not_bark', 1.0) \
.build()join_tree.set_observation(ev)
join_tree.set_observation(ev2)# print the marginal probabilities
for node in join_tree.get_bbn_nodes():
potential = join_tree.get_bbn_potential(node)
print(node)
print(potential)
print('--------------------->')
får vi följande resultat
0|season|winter,summer
0=winter|1.00000
0=summer|0.00000
--------------------->
2|allergies|allergic,non_alergic
2=allergic|0.70000
2=non_alergic|0.30000
--------------------->
3|rain|rainy,sunny
3=rainy|0.47059
3=sunny|0.52941
--------------------->
4|grass|grass,no_grass
4=grass|0.53529
4=no_grass|0.46471
--------------------->
1|atmos_press|high,low
1=high|0.39706
1=low|0.60294
--------------------->
5|umbrellas|on,off
5=on|0.88941
5=off|0.11059
--------------------->
6|dog_bark|bark,not_bark
6=bark|0.00000
6=not_bark|1.00000
--------------------->
7|cat_mood|good,bad
7=good|0.52647
7=bad|0.47353
--------------------->
8|cat_hide|hide,show
8=hide|0.83162
8=show|0.16838
--------------------->
Ser du skillnaden? 😆 Massor av sannolikhetsvärden förändrades när vi lade till beviset om skällandet. Det är definitivt ett fånigt exempel men trevligt att få intuition.
Hur använder man Bayesianska nätverk i SNA?
Bayesianska nätverk är mycket kraftfulla verktyg för att förstå strukturen för kausalitetsrelationer mellan variabler. När du väl har utformat din modell kan den, även med en liten datamängd, berätta olika saker för dig. Frågan i denna del är hur man kan dra nytta av Bayesian Nets i SNA. Svaret är inte unikt, men låt oss börja med en djupgående idé. I SNA försöker vi förstå strukturen i ett socialt nätverk. Dessutom försöker vi förstå nodernas betydelse. Men vi vet inte vad resultaten av våra mätningar av betydelsen är. Detta är den punkt där Bayesianska nätverk tar plats. Om man till exempel tror att betydelsen av en nod orsakas av Degree Centrality och Link Centrality kan man få följande nätverk:
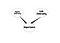
Detta är ett mycket naivt Bayesianskt nätverk. Förutom att bestämma nodernas betydelse kan ytterligare en tillämpning vara att söka efter vissa specifika typer av noder. Låt oss betrakta ett socialt nätverk där det finns några personer som är potentiella ledare och jag vill söka efter dem. Tänk på följande graf
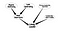
Detta lite mer komplicerade nätverk kommer att hjälpa oss att bestämma osäkerheten hos de noder som är relaterade till att vara ett ledarskap.
En annan tillämpning skulle kunna vara att härleda länkar. De nya länkarna kan härledas från befintliga länkar. Till exempel kan man från gruppmedlemskap i ett socialt nätverk dra slutsatser om sannolika medlemskapslänkar. Vad jag menade är att vi kan modellera en ny länk mellan användare och grupper genom att ta hänsyn till befintliga länkar. Se följande modelldiagram
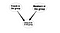
Så, detta är några grundläggande exempel på hur Bayesianska nätverk kan tillämpas i SNA. Detta ämne har inte studerats särskilt väl, men jag tror att det kan vara mycket användbart att studera vidare.
Slutsats
Det svåra med bayesianska nätverk är utformningen. Särskilt när man tänker på SNA är det mer konst än vetenskap att konstruera en kartläggning av det sociala nätverket med ett bayesianskt nätverk 😃 Men när man väl har gjort konstjobbet och konstruerat sin modell mycket väl kan dessa praktiska verktyg berätta en hel del saker för en. Som vi vet används bayesianska nätverk på många olika områden. Det har fungerat mycket bra i de flesta fall. Därför är jag övertygad om att vi kan göra mycket djupgående slutsatser om sociala nätverk också.
För ytterligare undersökningar med SNA och bayesianska nätverk, håll dig uppdaterad 🚀
.