Klassificering är en övervakad metod för maskininlärning, där algoritmen lär sig av de data som den får in – och sedan använder denna inlärning för att klassificera nya observationer.

Med andra ord används träningsdatasetetet för att få bättre gränsvillkor som kan användas för att bestämma varje målklass; när sådana gränsvillkor väl har bestämts är nästa uppgift att förutsäga målklassen.

Binära klassificerare arbetar med endast två klasser eller möjliga resultat (t.ex. positiva eller negativa känslor, om långivaren kommer att betala lånet eller inte, etc.), och flerklassiga klassificerare arbetar med flera klasser (t.ex. vilket land en flagga tillhör, om en bild är ett äpple, en banan eller en apelsin, etc.). Multiclass förutsätter att varje prov tilldelas en och endast en etikett.

En av de första populära algoritmerna för klassificering inom maskininlärning var Naive Bayes, en sannolikhetsklassificering som är inspirerad av Bayes-satsen (som gör det möjligt för oss att dra rimliga slutsatser om händelser som inträffar i verkligheten baserat på tidigare kunskaper om observationer som kan antyda det). Namnet (”Naive”) kommer från det faktum att algoritmen antar att attributen är villkorligt oberoende.

Algoritmen är enkel att implementera och utgör vanligtvis en rimlig metod för att starta ett klassificeringsarbete. Den kan lätt skalas till större datamängder (tar linjär tid jämfört med iterativ approximation, som används för många andra typer av klassificerare, vilket är dyrare i termer av beräkningsresurser) och kräver en liten mängd träningsdata.

Naive Bayes kan dock drabbas av ett problem som kallas ”nollprocentighetsproblem”, när den betingade sannolikheten är noll för ett visst attribut, vilket gör att det inte går att göra en giltig förutsägelse. En lösning är att utnyttja ett utjämningsförfarande (t.ex. Laplace-metoden).

P(c|x) är den efterföljande sannolikheten för klassen (c, mål) med tanke på förutsägelsefaktorn (x, attribut). P(c) är den tidigare sannolikheten för klassen. P(x|c) är sannolikheten som är sannolikheten för prediktor givet klass, och P(x) är den tidigare sannolikheten för prediktor.

Algoritmens första steg handlar om att beräkna den tidigare sannolikheten för givna klassbeteckningar. Därefter finner man sannolikheten för sannolikhet med varje attribut, för varje klass. Därefter sätts dessa värden in i Bayes-formeln & och man beräknar den efterföljande sannolikheten och ser sedan vilken klass som har en högre sannolikhet, givet att indata tillhör klassen med högre sannolikhet.

Det är ganska okomplicerat att implementera Naive Bayes i Python genom att utnyttja biblioteket scikit-learn. Det finns faktiskt tre typer av Naive Bayes-modeller i scikit-learn-biblioteket: (a) Gaussisk typ (antar att funktionerna följer en klockliknande normalfördelning), (b) Multinomial (används för diskreta räkningar, i form av antalet gånger ett resultat observeras i x försök) och (c) Bernoulli (användbar för binära funktionsvektorer; populärt användningsområde är textklassificering).

En annan populär mekanism är beslutsträdet. Med tanke på en data med attribut tillsammans med dess klasser producerar trädet en sekvens av regler som kan användas för att klassificera data. Algoritmen delar upp urvalet i två eller flera homogena uppsättningar (blad) baserat på de mest betydande differentieringarna i dina ingående variabler. För att välja en differentiator (prediktor) tar algoritmen hänsyn till alla egenskaper och gör en binär uppdelning på dem (för kategoriska data, dela upp efter kat; för kontinuerliga data, välj ett tröskelvärde). Den väljer sedan den med lägst kostnad (dvs. högsta noggrannhet) och upprepar sig rekursivt tills den lyckas dela upp data i alla blad (eller når det maximala djupet).

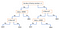
Dekisionsträd är generellt sett enkla att förstå och visualisera, och kräver lite dataförberedelser. Denna metod kan också hantera både numeriska och kategoriska data. Å andra sidan generaliserar komplexa träd inte bra (”overfitting”), och beslutsträd kan vara något instabila eftersom små variationer i data kan leda till att ett helt annat träd genereras.

En metod för klassificering som härstammar från beslutsträd är Random Forest, som i huvudsak är en ”meta-estimator” som anpassar ett antal beslutsträd på olika delprover av datamängder och använder genomsnittet för att förbättra modellens prediktiva noggrannhet och kontrollerar överanpassning. Delprovstorleken är densamma som den ursprungliga storleken på ingångsprovet – men proverna dras med ersättning.

Random Forests tenderar att uppvisa en högre grad av robusthet mot överanpassning (>robusthet mot brus i data), med en effektiv exekveringstid även i större dataset. De är dock mer känsliga för obalanserade dataset, men de är också lite mer komplexa att tolka och kräver mer beräkningsresurser.

En annan populär klassificerare inom ML är logistisk regression – där sannolikheter som beskriver de möjliga utfallen av en enskild prövning modelleras med hjälp av en logistisk funktion (klassificeringsmetod trots namnet):

Här ser den logistiska ekvationen ut:

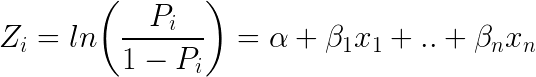
Om man tar e (exponent) på båda sidor av ekvationen får man följande resultat:

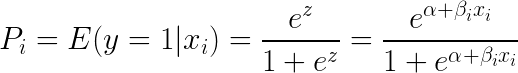
Logistisk regression är mest användbar för att förstå hur flera oberoende variabler påverkar en enda utfallsvariabel. Den är inriktad på binär klassificering (för problem med flera klasser använder vi utvidgningar av logistisk regression, t.ex. multinomial och ordinal logistisk regression). Logistisk regression är populär i flera användningsområden, t.ex. kreditanalys och benägenhet att reagera/köpa.

Sist men inte minst används kNN (för ”k Nearest Neighbors”) också ofta för klassificeringsproblem. kNN är en enkel algoritm som lagrar alla tillgängliga fall och klassificerar nya fall baserat på ett likhetsmått (t.ex. distansfunktioner). Den har använts inom statistisk uppskattning och mönsterigenkänning redan i början av 1970-talet som en icke-parametrisk teknik: