I dag ska vi lära oss primtalen från 1 till 100. I följande arbetsblad kan barn i grundskolan lära sig att identifiera primtal. Förutom att lära oss dem kommer vi också att göra några övningar med anknytning till dessa tal, divisorer, etc….

Vad är primtal?

Vad är primtal? Primtal är tal som endast kan divideras (utan decimaler i resultatet) med 1 och med sig själva. Det är omöjligt att beräkna dem, man måste lära sig dem. Kan man beräkna primtal? Nej, det finns ingen matematisk formel för att veta om ett tal är primtal eller inte.

Primtal är de tal som bara kan delas med 1 och med sig själva.

Men vi kan lära oss de första primtalen, till exempel i kvantiteterna från 1 till 100. Det finns också resurser för att ta reda på vilka tal som är primtal, t.ex. Eratosthenes sil, som vi kommer att se nedan.

Lista över primtal mellan 1 och 100:

2, 3, 5, 7, 11, 11, 13, 17, 17, 19, 19, 23, 23, 23, 29, 31, 37, 37, 37, 41, 43, 47, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89 och 97

För att identifiera primtal är det viktigt att känna till multiplikationstabellen, Du kan börja med att stryka de tal som kan multipliceras med 2, 3, 5 och 7 (vi utesluter t.ex. 4 och 6, eftersom de är multipler av primtalet 2). Denna metod för att få fram primtal kallas Eratosthenes’ sil (som vi kommer att se senare). Här är ett arbetsblad som barnen kan använda för att studera primtalen.

Primtalstabell

Vi har presenterat primtalen i form av en tabell, så att barnen alltid kan ha den till hands. Skriv ut den här tabellen så att barnen kan studera och lära sig primtalen från 1 till 100 på ett enkelt och visuellt sätt. De kan också använda tabellen över primtalen när de gör övningarna.

Den här tabellen nedan är ofärgad, så att barnen själva kan färglägga siffrorna eller göra Eratosthenes silning med den.

Övningar med primtal

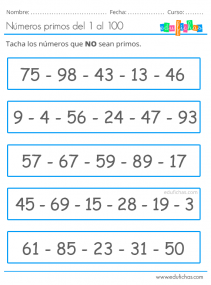
Efter att ha lärt sig primtalen med hjälp av tabellen ovan följer här några övningar där barnen kan öva på de kunskaper de har fått. Den första tabellen kan användas som en övning så att barnen, tack vare sina kunskaper om multiplikationstabellerna, kan stryka de tal som inte är primtal och lämna kvar de som är primtal. Kom ihåg att det är mycket användbart att veta hur man multiplicerar och dividerar för att barnen ska kunna göra övningarna.

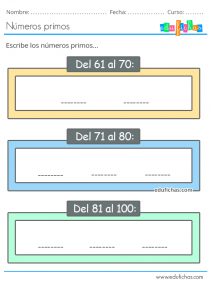De första korten kommer att hjälpa barnen att ha primesiffrorna från 1 till 100 till hands, ordnade efter tiotal. I varje ruta finns det utrymme för att skriva motsvarande siffror.

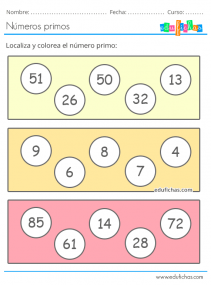
Sedan fortsätter vi med dessa övningar som ger oss rutor med siffror. I varje ruta finns fem tal, varav ett är ett primtal. Övningen går ut på att barnen ska identifiera den och färglägga den.

Primtalsuppgifter pdf

Primtalsuppgifter pdf

Primtalsuppgifter tal

Vårt aktivitetshäfte om primtal innehåller också fem sidor där barnen måste identifiera divisorerna. Om du vill ladda ner de enskilda arbetsbladen hittar du dem här.

Övningarna är utformade för elever i grundskolan. I det här avsnittet hittar du fler aktiviteter för grundskolan.

Eratosthenes’ sikte

Eratosthenes’ sikte är en fantastisk övning för grundskolebarn för att lära sig att identifiera primtalen från 1 till 100. Eratosthenes var en gammal grekisk matematiker som uppfann ett sätt att få fram primtalen. Han kallade det Eratosthenes sikte, och det går ut på att göra en tabell med tal från 1 till 100 för att ta reda på vilka som är primtal.

Detta är mallen för att göra ett Eratosthenes sikte och sedan förklarar vi hur man får fram primtalen härifrån. Vi stryker över de som inte är primtal och färglägger in de som är primtal.

Du kan använda vår tabell (du hittar den ovan), med omärkta tal från 1 till 100, så att barnen kan använda Eratosthenes’ sikte som en övning för att lära sig primtal. Dessutom hjälper det dem att repetera multiplikationstabellerna, eftersom de måste stryka över de multiplar av talen som motsvarar resultaten i multiplikationstabellerna.

För att göra Eratosthenes tabellövning på rätt sätt kan barnen följa följande steg.

1. Hitta multiplarna av 2 (låt 2 vara omarkerat, eftersom det är ett primtal).
2. Gör samma sak med multiplarna av 3 (låt 3 vara omarkerat, eftersom det också är ett primtal).
3. Talet 4 kommer redan att vara överstruket (det är en multipel av 2), så vi behöver inte göra något.
4. Hitta multiplarna av 5 (vi låter talet 5 vara omarkerat eftersom det är ett primtal).
5. Vi hoppar över 6 eftersom det kommer att vara överstruket, av samma anledning som 4.
6. Hitta multiplarna av 7 och låt 7 vara omarkerat eftersom det är ett primtal.
7. Vi hoppar över 8 (eftersom det är en multipel av 2 och 4).
8. Därefter hoppar vi över 9 (eftersom det är en multipel av 3).
9. Vi hoppar över 10 (eftersom det är en multipel av 2 och 5).
10. Vi letar efter multiplar av talet 11.

Och då är vi klara. Alla tal som inte har strukits är primtal. Om du vill veta mer om denna metod kan du läsa det här inlägget om Eratosthenes.

Aktivitetshäfte om primtal

Ladda ner aktivitetshäftet om primtal i PDF. Tack vare den här filen kan du ha och skriva ut alla arbetsblad på den här sidan från en enda fil. Det är det bekvämaste sättet om du vill göra alla övningar. Du hittar filen på den här länken.

Ladda ner PDF

Primitiva tal är nödvändiga när du ska räkna ut den största gemensamma divisorn och den minsta gemensamma multipeln. För att göra detta utför vi en primfaktordekomposition, som består av att dividera talen med primtalen som utdelning, tills vi får 1 som resultat. Om du vill lära dig mer om primtal rekommenderar vi att du läser denna publikation Yo Soy Tu Profe, som handlar om hur man vet om ett tal är ett primtal eller inte, samt en hel del information för att förstå dem bättre.

Vi har också förberett en kort video som visar dig den här anteckningsboken på vår YouTube-kanal. Om du vill se våra videor om anteckningsböcker kan du prenumerera på vår YouTube-kanal.