(IUCr) Symboler för symmetrielement

Acta Cryst. (1992). A48, 727-732

Final report of the International Union of Crystallography Ad-Hoc Committee on the nomenclature of symmetry*

av P. M. DE WOLFF (ordförande), Meermanstraat 126, 2614 AM Delft, Nederländerna,

Y. BILLIET, Ecole Nationale d’Ingénieurs, BPW 3038 Sfax, Tunesien,

J. D. H. DONNAY, Department of Geological Sciences, McGill University, 3450 University Street, Montreal, Canada H3A 2A7,

W. FISCHER, Institut für Mineralogie, Petrologie und Kristallographie der Phillips-Universität, Lahnberge, D-3550 Marburg (Lahn), Tyskland,

R. B. GALIULIN, Institute of Crystallography, Academy of Sciences of Russia, Leninsky Prospekt 59, Moscow 117333, Russia,

A. M. GLAZER, Clarendon Laboratory, University of Oxford, Parks Road, Oxford OX1 3PU England,

TH. HAHN, Institut für Kristallographie, RWTH, Templergraben 55, D-5100 Aachen, Tyskland,

MARJORIE SENECHAL, Department of Mathematics, Smith College, Northampton, MA 01063, USA,

D. P. SHOEMAKER, Chemistry Department, Oregon State University, OR 97331, USA,

H. WONDRATSCHEK, Institut für Kristallographie, Universität Karlsruhe, Kaiserstrasse 12, D-7500 Karlsruhe 1, Tyskland,

A. J. C. WILSON (ex officio, IUCr Commission on International Tables), Crystallographic Data Centre, University Chemistry Laboratory, Lensfield Road, Cambridge CB2 1EW, England

OCH S. C. ABRAHAMS (ex officio, IUCr Commission on Crystallographic Nomenclature), Department of Physics, Southern Oregon State College, 1250 Siskiyou Boulevard, Ashland, OR 97520-5047, USA

(Mottagen den 7 november 1991; accepterad den 9 mars 1992)

* Utnämnd den 14 november 1984, ändrad den 10 augusti 1987 i enlighet med de regler som beskrivs i Acta Cryst. (1979), A35, 1072. Slutrapport accepterad den 23 december 1991 av IUCr:s kommission för kristallografisk nomenklatur och den 9 mars 1992 av den verkställande kommittén.

Abstract

Nya eller omdefinierade tryckta symboler föreslås mot bakgrund av den nyligen accepterade omdefinitionen av symmetrielement . Särskilt bokstaven e täcker vissa glidplan som hittills inte haft någon unik symbol, t.ex. de som kallas ”antingen a eller b”. Användningen av e i Hermann-Mauguin-symbolen för fem olika rymdgrupper rekommenderas. För e-flygplan som projiceras i en riktning parallellt med planet föreslås en grafisk symbol som undanröjer tvetydigheten i deras nuvarande beteckning. Bokstaven k föreslås för en nydefinierad klass av glidflygplan som hittills inte haft någon särskild symbol. De symboler för symmetrioperationer som infördes i rymdgruppsbeskrivningarna i International Tables for Crystallography (1989), Vol. A (Dordrecht: Kluwer Academic Publishers) rekommenderas för allmän användning, med ändringar endast för glidspegeloperationer.

Introduktion

Den ad hoc-kommitté som utsågs 1980 för att överväga ”nomenklaturproblem rörande symmetrioperationer och symmetrielement i rymdgrupper” har utfärdat två rapporter med titeln Nomenklatur för kristallfamiljer, Bravais-Lattice-typer och aritmetiska klasser (de Wolff et al, 1985) och Definition of Symmetry Elements in Space Groups and Point Groups (de Wolff et al., 1989). Såsom noterades i 1989 års rapport är det enda kvarstående problemet när det gäller symmetrioperationer att välja lämpliga symboler, eftersom begreppet är tydligt. En provisorisk notation har antagits i International Tables for Crystallography (1983, 1989), nedan kallad ITA83.

Tryckta symboler för symmetrielement

Den definition av symmetrielement som ges i 1989 års rapport (de Wolff et al.) kommer att användas i hela denna rapport. Här upprepar vi kärnan:

För varje given symmetrioperation definieras dess geometriska element (plan, punkt och/eller linje). Ett symmetrielement är kombinationen av det geometriska elementet för en av symmetrioperationerna i en given rumsgrupp med uppsättningen (kallad ”elementuppsättning”) av alla symmetrioperationer i den rumsgruppen som delar detta geometriska element.

Explicita definitioner av geometriska element och beskrivningar av de resulterande symmetrielementen samt deras symboler ges i tabellerna 1 och 2. (Dessa är identiska med tabellerna 1 och 2 i 1989 års rapport, med undantag av glidplan, och upprepas här för fullständighetens skull, se nedan). Varje symmetrielement representeras av en symbol som består av två tecken. Det första tecknet är ett stort E för alla symmetrielement. Det visar att symbolen avser ett symmetrielement och inte t.ex. en symmetrioperation. Om detta framgår redan av sammanhanget kan E:et utelämnas, t.ex. ”en axel 2” i stället för ”en axel E2”.

Tabell 1. Geometriska element för symmetrioperationer i punktgrupper och rumsgrupper
Symmetrioperation	Geometriskt element	Tillkommande parametrar
Identitet	Inte nödvändigt	Inte
Translation	Inte nödvändigt	Vektor $\mathbf{t}$
Reflexion i plan A	Plan A	Ingen
Glidreflektion =reflektion i plan A och translation $\mathbf{v}$ parallellt med A	Plan A	Glidvektor $\mathbf{v}$
Rotation kring linje b	Linje b	Vinkel och rotationsriktning
Skruvrotation = rotation runt linje b och translation $\mathbf{u}$ parallellt med b	Linje b	Vinkel och riktning för rotationsskruvvektor $\mathbf{u}$
Rotoinversion = rotation kring linje b och inversion genom punkt P på b	Linje b och punkt P på b	Vinkel (ej lika med $\pi$ ) och rotationsriktning
Inversion genom punkt P	Punkt P	Ingen

Symbolen Eg som anges i 1989 års rapport kan användas för glidplan om man bara vill visa att symmetrielementet är ett glidplan. Om det däremot tillhör en av de speciella typer som sedan länge betecknas med en lämplig bokstav (a, b, c, n eller d; jfr ITA83), ersätter den bokstaven g i Eg.

Tabell 2. Symmetrielement i punktgrupper och rumsgrupper
Namn på symmetrielementet	Symbol	Geometriskt element	Definitionsoperation (d.o.)	Operationer i elementmängd
Spegelplan	Em	Plan A	Reflexion i A	D.o. och dess koplanära motsvarigheter*
Glidplan	Eg $\ddag$	Plan A	Glidreflektion i A, 2v (inte v) en gittertranslation	D.o. och dess koplanära motsvarigheter*
Rotationsaxel	En	Linje b	Rotation om b, vinkel $2\pi/n$ ,n = 2, 3, 4 eller 6	1:a, $\dots$ ,(n – 1)e potenser av d.o. och deras koaxiala motsvarigheter\dag
Skruvens axel	Enj	Linje b	Skruvens rotation runt b, vinkel $2\pi/n$ , u =j/n gånger kortaste gitter translation längs b, högerskruv; n = 2, 3, 4 eller 6, $j=1,\dots,(n-1)$	1st, $\dots$ ,(n – 1)th powers of d.o. och deras koaxiala motsvarigheter\dag
Rotoinversionsaxel	$E\bar n$	Linje b och punkten P på b	Rotoinvertering: rotation om b, vinkel $2\pi/n$ , och omvändning genom P; n = 3, 4 eller 6	D.o. och dess invers
Center	$E\bar 1$	Punkt P	Inversion genom P	D.o. only

* Det vill säga alla glidreflektioner med samma reflektionsplan, med glidvektorer som skiljer sig från d.o.-vektorerna (som antas vara noll för en reflektion) med en gittertranslationsvektor.
\dag Det vill säga alla rotationer och skruvrotationer med samma axel b, samma vinkel och rotationsriktning och samma skruvvektor $\mathbf{u}$ (noll för en rotation) upp till en gittertranslationsvektor.
$\ddag$ I Eg ersätts g med a, b, c, n, d, e eller k för specifika typer av glidplan, jfr §2.

En viktig ny aspekt av symboler som Eb kan dock påpekas. Enligt ITA83 innebar beteckning av ett plan med b endast att en glidreflektion i planet med en glidkomponent b/2 längs b-axeln är en symmetrioperation. Denna definition gäller förvisso för den situation som avbildas i fig. 1.

Fig. 1. (Efter W. Fischer.) Elementmängden i ett Eb-glidplan, som visas som en uppsättning punkter över (+) och under (-) planet som produceras av glidreflektioner i planet, till exempel med utgångspunkt i +-tecknet uppe till vänster. Nettot N av translationer parallellt med planet (+$\cdots$ + vektorer) anges av en mask, som i det här fallet råkar vara rektangulär. Båda paren av kanter är parallella med kristallaxlarna. Det finns en glidreflektion med sin glidvektor (+ $\cdots$ -) längs b-axeln.

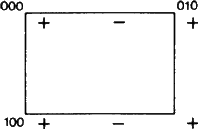
$\begin{figure} \includegraphics {fig1.ps} \end{figure}$

Figur 1 är anpassad, liksom figurerna 2 och 3, från en uppsättning liknande figurer som utformats av Ad-hoc-kommitténs medlem W. Fischer som en inventering av alla typer av glidplan. Även om uppsättningen presenterades för kommittén 1980, långt innan 1989 års rapport kom ut, visar var och en av dess figurer exakt ”elementuppsättningen” av glidflygplanet enligt definitionen i den rapporten (se sammanfattningen ovan). För ett glidplan består elementmängden av alla glidreflektioner som har planet som gemensamt geometriskt element. Deras verkan visas i projektion på detta plan. Från startpositionen för varje +-tecken är varje -tecken ett resultat av en av glidreflektionerna i mängden. Alla dessa visas inom ett elementärt nät av det resulterande tvådimensionella periodiska mönstret av +- och -tecken.

Vi kommer ofta att hänvisa till det nät N som bildas av alla translationer parallellt med planet; detta nät kan lätt visualiseras genom att endast titta på +-tecken. Dessa vektorer ska skiljas skarpt från de vektorer som förbinder ett +-tecken med något -tecken, som var och en är glidvektor för en glidreflektion som tillhör elementmängden.

Den nya aspekten uppstår eftersom b-glidplanet enligt ITA83-definitionen i vissa fall också är ett a-glidplan, se fig. 2. Det är uppenbart att detta endast sker om nätet N är ortogonalt centrerat, eftersom a-glidet då kan ändras till ett b-glid (och vice versa) genom att lägga till en centrerande translation. Hittills har praxis varit att godtyckligt kalla ett sådant glidplan för antingen a eller b, vilket leder till en omotiverad bias och en brist på entydighet i dessa symboler. Vi föreslår därför att fallet i figur 2 ska omfattas av en separat symbol.

Fig. 2. (Efter W. Fischer.) Elementmängden för ett Ee-glidplan. Jfr. bildtexten till fig. 1. Observera att nätet N här är ortogonalt centrerat.

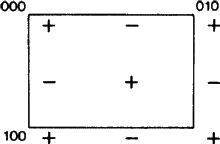
$\begin{figure} \includegraphics {fig2.ps} \end{figure}$

Symbolens räckvidd bör då utvidgas till att omfatta glidplan i diagonal orientering, det vill säga parallellt med bara en kristallaxel, förutsatt att glidplanet har en glidvektor längs den axeln och att nätet N är ortogonalt centrerat. För sådana plan finns inte tvetydigheten i det ovan nämnda slumpmässiga valet a-b, utan den nya symbolens utvidgade räckvidd ligger i linje med räckvidden för alla befintliga symboler (nämligen a, b, c, n och d). Var och en av dessa används för ett glidplan med både en och två kristallaxlar i nätet N, jfr figur 3.

Bokstaven e föreslås för den nya symbolen. Ee kommer således att gälla för glidplan med ortogonala centrerade nät N och minst en glidvektor längs en kristallaxel. Ett nytt kriterium är därför nödvändigt: nämligen glidvektorernas orientering i förhållande till kristallens konventionella axlar. Eftersom dessa ligger längs symmetririktningar, medan varje glidplan är parallellt med ett spegelplan i gittret, är det inte förvånande att det alltid finns minst en konventionell kristallaxel i N. Om det bara finns en sådan axel finns det alltid en annan translation i N vinkelrätt mot den.

Den nya symbolen e samt de gamla symbolerna a, b, c, d, n kommer nu att omdefinieras utifrån detta nya kriterium och Bravais-nätets typ N. Detta nät är monoklin eller ortogonalt eller tetragonalt primitivt (mp eller op eller tp) eller ortogonalt centrerat (oc). Endast nät N av oc-typ tillåter ett Ee-glidplan. Symbolen En är tillämplig på nät N av Bravais-typ mp eller op, medan Ed är tillämplig på nät N av oc-typ. (Som anges i en fotnot till tabell 1.3 i ITA83: ”Glidplan d förekommer endast i ortorhombiska F-rumgrupper, i tetragonala I-rumgrupper och i kubiska I- och F-rumgrupper. De förekommer alltid i par med alternerande glidvektorer”). I motsats till planerna Ea, Eb, Ec och Ee finns det dock för planerna En och Ed ingen glidvektor som är vare sig parallell eller vinkelrät mot en konventionell axel i N.

De följande definitionerna av glidplanen av ovanstående slag sammanfattas i raderna (i) och (ii) i tabell 3, och mer explicit i figur 3.

Tabell 3. Tryckta symboler för särskilda typer av glidflygplan
Antal glidvektorer som är parallella eller vinkelräta mot kristallaxlarna i nät N	Bravais typ av nät N
Symbolen bestäms av två kriterier. Det ena kriteriet är Bravais-typen (mp, op, tp eller oc) av det nät N som bildas av de symmetritranslationer som är parallella med det aktuella planet. Detta nät innehåller alltid minst en konventionell kristallaxel.* Det andra kriteriet avser glidvektorernas orientering i förhållande till sådana axlar.
	m, op, tp	oc
(i) En eller två parallella	Ec(Ea, Eb)	Ee
(ii) Ingen parallell, ingen vinkelrät	En	Ed
(iii) Ingen parallell, en vinkelrät	Ek	–

* Enligt definitionen i ITA83, § 9.1; för rombosedriska rymdgrupper används dock endast hexagonala axlar här.

Alla återstående glidflygplan var tidigare utan särskild symbol. De har var och en en diagonal orientering (bara en konventionell kristallaxel i nätet N). Bland glidreflektionerna i deras elementuppsättning finns det ingen med en glidvektor längs den axeln. En glidvektor är dock (genom symmetri) vinkelrät mot den. En symbol verkar önskvärd, så återigen föreslås en ny bokstav: k. Den nya symbolen Ek definieras kortfattat i rad (iii) i tabell 3 och illustreras fullständigt i det nedre blocket i figur 3. Några exempel ges i punkt 2.

Fig. 3. (Anpassad från W. Fishers ritningar.) Alla möjliga aspekter av elementuppsättningarna av glidplan som visas som i figur 1, men oberoende av axelbeteckningar. Diagrammen är grupperade i kolumner som leds av symbolen av Bravais-nettyp (översta raden) för deras nät N, se tabell 3. De övriga kriterierna i tabellen kontrolleras genom att först titta på de dubbla linjerna som visar kristallaxlarnas riktningar i planet. En kant (vertikal) av det visade nätet N väljs alltid längs en sådan axel. Den andra kanten är horisontell utom i (1) och (8). För diagrammen (1), $\dots$ ,(5) är symbolen för glidplanet etiketten a, b eller c för den vertikala axeln; för de andra är det den inringade bokstaven i det omskrivna blocket som innehåller diagrammet. Observera de vertikala glidbanevektorerna i diagrammen (1), $\dots$ ,(7), de horisontella i (6), (7), (14), (15) och avsaknaden av någon av dem i (8), $\dots$ ,(13). Ett exempel på förekomst anges under varje diagram med rumsgruppssymbolen och planets koordinattrippel.

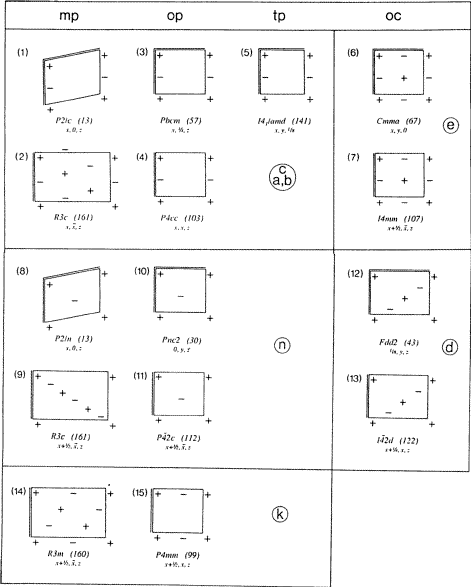
$\begin{figure} \includegraphics {fig3.ps} \end{figure}$

I figur 3 visas Fischers inventering av alla typer av glidplan på ett förkortat – om än fortfarande fullständigt – sätt där kristallaxlarna har fått större grafisk betydelse. För varje diagram listas ett exempel på dess förekomst i en rumsgrupp.

I vissa rombosedriska rumsgrupper förekommer diagonalt orienterade Ec-, En- och Ek-plan med nät av mp-typ N som kan beskrivas genom trefaldig centrering av ett ortogonalt nät. En rektangulär trippelmask av nätet N visas för dessa typer av glidplan i figur 3, diagrammen (2), (9) och (14). I diagram (9) känns likheten med andra n-diagram som (8) eller (10) igen om man i (9) betraktar en monoklin primitiv mask av nätet N med diagonala glidvektorer.

Grafiska symboler för symmetrielement

De existerande grafiska symbolerna såsom de definierats och använts i ITA83 anses vara adekvata av ad hoc-kommittén med ett undantag. Situationen skiljer sig mycket från den för tryckta symboler eftersom projektionsriktningen i ritningar blir en extra parameter. I termerna ’vinkelrätt projektion’ och ’parallell projektion’ som används nedan, avser vinkelrätt och parallell projektionsriktningens orientering i förhållande till glidplanet.

För ett Ee-plan finns symbolen 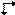för dess vinkelrätt projektion. De befintliga grafiska symbolerna för den parallella projektionen av ett Ee-glidplan lider dock av samma tvetydighet som de tryckta symbolerna. De uttrycker glidvektorn antingen parallellt eller vinkelrätt mot projektionsriktningen, men valet är godtyckligt. Därför föreslås en ny symbol för den parallella projektionen av ett Ee-glidplan, nämligen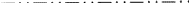

Exempel på Ee-plan.

Alla glidplan som är parallella med två axlar i rumsgrupperna Fmm2, Fmmm, $Fm\bar 3$ , $Fm\bar 3m$ och $Fm\bar 3c$ (nr 42, 69, 202, 225 och 226), samt vissa plan i de fem rumsgrupper som förtecknas i §3.

Diagonalt orienterade Ee-plan förekommer i rymdgrupperna I4mm, I4cm, $I\bar 42m$ , I4/mmm, I4/mcm, $I\bar 43m$ och $Im\bar 3m$ (nr. 107, 108, 121, 139, 140, 217 och 229).

I ITA83 ritas alla dessa Ee-plan ganska godtyckligt som antingen streckade eller streckade linjer i deras parallella projektioner. Fig. 4 visar diagrammet för rymdgrupp I4cm (nr 108), både som det visas i ITA83 och med användning av den nya symbolen.

Fig. 4. (a) Diagram över rymdgrupp I4cm (nr 108) från ITA83. (b) Samma, modifierat genom användning av den grafiska symbol som föreslås i § 2, för parallellprojektionen av ett Ee-plan.

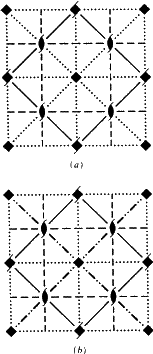
$\begin{figure} \includegraphics {fig4.ps} \end{figure}$

Om än Ek är en ny trycksymbol har i diagrammen i ITA83 alla glidplan Ek ritats på ett tillfredsställande sätt med samma konventioner som används för Ea/b/c glidplan. Liksom i dessa fall finns det en enda speciell glidvektor (vinkelrätt mot kristallaxeln i nät N, se tabell 3). När denna vektor till exempel är parallell med projektionsplanet ritas Ek-planet alltid som den streckade linje som föreskrivs i den relevanta konventionen. Därför föreslås ingen ny grafisk symbol för Ek-glidplan.

Exempel på Ek-plan.

Sådana plan återfinns lätt i diagrammen i ITA83 som plan parallella med endast en axel och projicerade som streckade linjer, t.ex. xxz i P4bm och $P\bar 42_1m$ (nr 100 och 113). Särskilt tabell 3 stämmer exakt överens med den skillnad som visas mellan Ek- och En-plan. Se till exempel de streckade och punktstreckade linjerna för R3m och R3c (nr 160 och 161).

Hermann-Mauguin-rumgruppsymboler

De tecken som förekommer efter gitterbokstaven i Hermann-Mauguin-symbolen (HM) för en rymdgrupp var ursprungligen tänkta att representera genererande operationer för gruppen. Till exempel var b en b-glidreflektion i ett plan orienterat enligt dess position i HM-symbolen.

I praktiken tog de populära men dåligt definierade symmetrielementen över från operationerna. Således kom b att ses som ett glidplan, Eb i vår nuvarande terminologi. Det finns ingen skada i denna omtolkning utom när operationen hör till ett Ee-glidplan. Om detta gäller, t.ex. för den ovan nämnda b-gliderspeglingen, finns det ett Ee- men inget Eb-glidplan i motsvarande orientering. I detta fall blir b ett mycket missvisande tecken. Bortsett från detta är den fördom (som ges till b framför a eller c) lika störande som i fallet med symmetrielement-symbolerna som behandlas i §1.

Det föreslås därför att sådana vilseledande bokstäver a eller b ersätts med e i alla de fem HM-symboler där de förekommer:

Rymdgrupp nr.	39	41	64	67	68
Symbol i ITA83:	Abm2	Aba2	Cmca	Cmma	Ccca
Ny symbol:	Aem2	Aea2	Cmce	Cmme	Ccce.

En ytterligare fördel med de föreslagna nya symbolerna är att e – till skillnad från a eller b – är neutralt och därför inte ändras vid axelpermutation.

Tryckta symboler för symmetrioperationer

En komplett uppsättning tryckta symboler utformades av W. Fischer & E. Koch (ITA83, §11.2) och tillämpades i stor utsträckning i avsnitten om symmetrioperationer i rumsgruppsbeskrivningarna.

Samt sett består varje symbol av upp till tre delar. Den första delen är ett enskilt tecken (ibland med ett index) som beskriver typen av operation. Den eller de följande delarna ger komponenterna för varje relevant förskjutnings- eller translationsvektor – alltid inom parentes – och koordinaterna för operationens geometriska element, i den ordningen.

Ad hoc-kommittén vill, efter att ha övervägt detta system, införa två ändringar för glidreflektioner:

(i) i stället för det nuvarande första tecknet (som kan vara a, b, c, n, d eller g), skriv alltid bokstaven g;

(ii) skriv alltid glidvektorkomponenterna (inom parenteser) i sin helhet, i synnerhet för de enkla glidreflektioner i a-, b- eller c-glidplan där de tidigare utelämnades.

Regel (i) undertrycker information om vilken typ av glidplan som operationen tillhör. Mycket ofta är denna information irrelevant eller till och med förvirrande. För a/b/c-plan kan borttagandet förstöra viktig information, men förlusten återställs genom regel (ii) som visas i exemplet nedan.

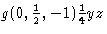Med hjälp av dessa ändringar förbättras enhetligheten hos symbolerna – även med avseende på symbolerna för rotationer – avsevärt. Till exempel symbolen för glidreflektionen i planet $x = \frac{1}{4}$ , med den ovanliga glidvektorn $(0, \frac{1}{2}, -1)$ , nämligen $g(0, \frac{1}{2}, 1) \frac{1}{4}yz$ , hamnar nu i linje med symbolen för en enkel b-glidreflektion. I ITA83 betecknades den senare med $b \frac{1}{4} y z$ , men detta ändras genom regel (ii) till $g(0, \frac{1}{2}, 0) \frac{1}{4} y z$ .

Ovanstående regler gäller även för glidreflektioner som tillhör elementmängden för ett spegelplan. Om skiftkomponenten för en sådan operation således är (0, 1, 2) börjar dess symbol med g(0, 1, 2), inte med m(0, 1,2).

International Tables for Crystallography (1983). Vol. A, redigerad av TH. HAHN, särskilt §§ 1.1, 1.3, 1.4, 7 och 11. Dordrecht: Kluwer Academic Publishers.

International Tables for Crystallography (1989). Vol. A, 2nd, revised, ed., redigerad av TH. HAHN. Dordrecht: Kluwer Academic Publishers.

WOLFF, P. M. DE, BELOV, N. V., BERTAUT, E. F., BUERGER, M. J., DONNAY, J. D. H., FISCHER, W., HAHN, TH., KOPTSIK, V. A., MACKAY, A. L., WONDRATSCHEK, H., WILSON, A. J. C. & ABRAHAMS, S. C. (1985). Acta Cryst. A41, 278-280.

WOLFF, P. M. DE, BILLIET, Y., DONNAY, J. D. H., FISCHER, W., GALIULIN, R. B., GLAZER, A. M., SENECHAL, M., SHOEMAKER, D. P., WONDRATSCHEK, H., HAHN, TH., WILSON, A. J. C. & ABRAHAMS, S. C. (1989). Acta Cryst. A45, 494-499.

…vektorer. Glidplanssymbolerna c, n och k för de tre diagrammen (2), (9) och (14) i figur 3 har naturligtvis tilldelats i enlighet med tabell 3. En medlem av ad hoc-kommittén (professor Wondratschek) anser att symbolen n för diagram (9) strider mot traditionella föreställningar om n plan. Han föreslår att diagram (9) tilldelas en särskild symbol. Detta förslag har dock inte fått tillräckligt stöd inom ad hoc-kommittén.

Symboler för symmetrielement och symmetrioperationer