Mimo że metody z poprzedniej sekcji są przydatne do opisywania i wyświetlania danych z próbek, prawdziwa moc statystyki ujawnia się, gdy używamy próbek do dostarczenia nam informacji o populacjach. W tym kontekście, populacja to cały zbiór obiektów zainteresowania, na przykład, ceny sprzedaży wszystkich domów jednorodzinnych na rynku mieszkaniowym reprezentowanym przez nasz zbiór danych. Chcielibyśmy wiedzieć więcej o tej populacji, aby pomóc nam podjąć decyzję o tym, który dom kupić, ale jedyne dane, jakie mamy, to losowa próbka 30 cen sprzedaży.
Niemniej jednak, możemy zastosować „myślenie statystyczne”, aby wyciągnąć wnioski na temat interesującej nas populacji poprzez analizę danych z próbki. W szczególności, używamy pojęcia modelu – matematycznej abstrakcji rzeczywistego świata – który dopasowujemy do danych z próbki. Jeśli ten model zapewnia rozsądne dopasowanie do danych, to znaczy, jeśli może on przybliżać sposób, w jaki dane się zmieniają, wtedy zakładamy, że może on również przybliżać zachowanie populacji. Model stanowi wówczas podstawę do podejmowania decyzji dotyczących populacji, na przykład poprzez identyfikację wzorców, wyjaśnianie zmienności i przewidywanie przyszłych wartości. Oczywiście, ten proces może działać tylko wtedy, gdy dane z próbki można uznać za reprezentatywne dla populacji.
Czasami, nawet gdy wiemy, że próbka nie została wybrana losowo, nadal możemy ją modelować. Wtedy, możemy nie być w stanie formalnie wnioskować o populacji na podstawie próbki, ale nadal możemy modelować podstawową strukturę próbki. Przykładem może być próba wygodna – próba wybrana bardziej ze względu na wygodę niż na jej właściwości statystyczne. Kiedy modelujemy takie próby, wszelkie wyniki powinny być raportowane z ostrzeżeniem o ograniczaniu wszelkich wniosków do obiektów podobnych do tych w próbie. Innym rodzajem przykładu jest sytuacja, gdy próba obejmuje całą populację. Na przykład, moglibyśmy modelować dane dla wszystkich 50 stanów Stanów Zjednoczonych Ameryki, aby lepiej zrozumieć wszelkie wzorce lub systematyczne związki między stanami.
Ponieważ świat rzeczywisty może być niezwykle skomplikowany (w sposób, w jaki wartości danych różnią się lub oddziałują na siebie), modele są użyteczne, ponieważ upraszczają problemy tak, że możemy je lepiej zrozumieć (a następnie podjąć bardziej skuteczne decyzje). Z jednej strony, potrzebujemy więc modeli na tyle prostych, abyśmy mogli z łatwością wykorzystywać je do podejmowania decyzji, ale z drugiej strony, potrzebujemy modeli, które są na tyle elastyczne, aby zapewnić dobre przybliżenia złożonych sytuacji. Na szczęście, na przestrzeni lat opracowano wiele modeli statystycznych, które zapewniają skuteczną równowagę pomiędzy tymi dwoma kryteriami. Jednym z takich modeli, który stanowi dobry punkt wyjścia dla bardziej skomplikowanych modeli, które rozważymy później, jest rozkład normalny.
Z punktu widzenia statystyki, rozkład prawdopodobieństwa jest modelem teoretycznym, który opisuje, jak zmienna losowa zmienia się. Dla naszych celów, zmienna losowa reprezentuje interesujące nas wartości danych w populacji, na przykład, ceny sprzedaży wszystkich domów jednorodzinnych na naszym rynku mieszkaniowym. Jednym ze sposobów przedstawienia rozkładu wartości danych w populacji jest histogram, jak opisano w rozdziale 1.1. Różnica polega na tym, że histogram wyświetla całą populację, a nie tylko próbkę. Ponieważ populacja jest znacznie większa niż próbka, biny histogramu (kolejne zakresy danych, które tworzą poziome przedziały dla słupków) mogą być znacznie mniejsze, na przykład, poniżej pokazany jest histogram dla symulowanej populacji 1000 cen sprzedaży.
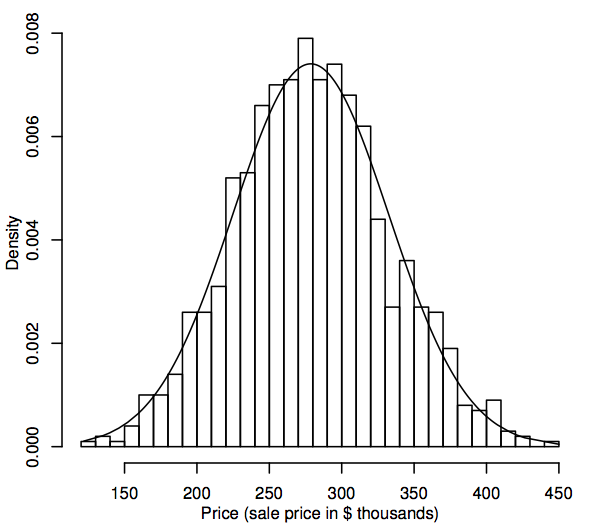
Jak wielkość populacji staje się większa, możemy sobie wyobrazić, że słupki histogramu stają się coraz cieńsze i liczniejsze, aż histogram przypomina raczej gładką krzywą niż serię kroków. Ta gładka krzywa nazywana jest krzywą gęstości i można o niej myśleć jak o teoretycznej wersji histogramu populacji. Krzywe gęstości pozwalają również na wizualizację rozkładów prawdopodobieństwa, takich jak rozkład normalny. Normalna krzywa gęstości jest nałożona na powyższy histogram. Symulowany histogram populacji podąża za krzywą dość blisko, co sugeruje, że ten symulowany rozkład populacji jest dość bliski normalnemu.
Aby zobaczyć, jak teoretyczny rozkład może okazać się przydatny do wnioskowania statystycznego o populacjach takich jak ta w naszym przykładzie cen domów, musimy przyjrzeć się bliżej rozkładowi normalnemu. Na początek rozważymy konkretną wersję rozkładu normalnego, standardową normalną, reprezentowaną przez następującą krzywą gęstości.
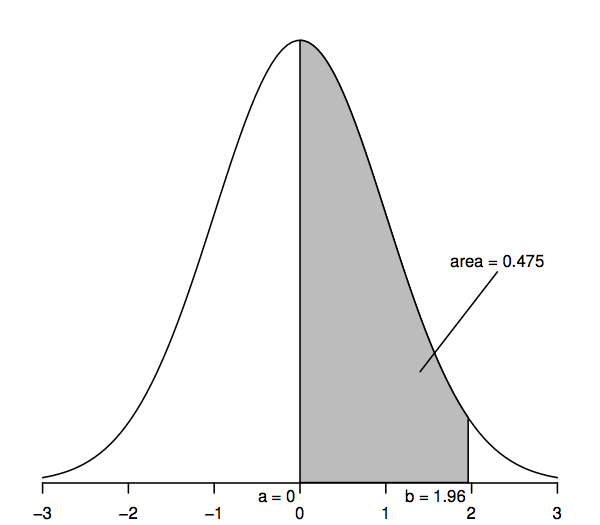
Zmienne losowe, które podążają za standardowym rozkładem normalnym mają średnią 0 (więc krzywa jest symetryczna wokół 0, które znajduje się pod najwyższym punktem krzywej) i odchylenie standardowe 1 (więc krzywa ma punkt przegięcia – gdzie krzywa wygina się najpierw w jedną, a potem w drugą stronę – przy +1 i -1). Normalna krzywa gęstości jest czasami nazywana „krzywą dzwonową”, ponieważ jej kształt przypomina dzwon.
Kluczową cechą normalnej krzywej gęstości, która pozwala nam na wnioskowanie statystyczne, jest to, że obszary pod krzywą reprezentują prawdopodobieństwa. Cały obszar pod krzywą to jeden, podczas gdy obszar pod krzywą między jednym punktem na osi poziomej (a, powiedzmy) i innym punktem (b, powiedzmy) reprezentuje prawdopodobieństwo, że zmienna losowa, która podąża za standardowym rozkładem normalnym znajduje się między a i b. Tak więc, na przykład, powyższy rysunek pokazuje, że prawdopodobieństwo wynosi 0.475 że standardowa normalna zmienna losowa leży między a=0 i b=1.96, ponieważ obszar pod krzywą między a=0 i b=1.96 jest 0.475.
Możemy uzyskać wartości dla tych obszarów lub prawdopodobieństwa z różnych źródeł: tabele liczb, kalkulatory, arkusze kalkulacyjne lub oprogramowanie statystyczne, strony internetowe, i tak dalej. Poniżej drukujemy tylko kilka wybranych wartości, ponieważ większość późniejszych obliczeń wykorzystuje uogólnienie rozkładu normalnego zwane „rozkładem t”. Ponadto, zamiast obszarów takich jak ten zacieniony na powyższym rysunku, bardziej użyteczne stanie się rozważenie „obszarów ogona” (np, na prawo od punktu b), a zatem dla zachowania spójności z późniejszymi tabelami liczb, poniższa tabela umożliwia obliczanie takich obszarów ogonowych:
W szczególności, obszar górnego ogona na prawo od 1,96 wynosi 0,025; jest to równoważne stwierdzeniu, że obszar pomiędzy 0 a 1,96 wynosi 0,475 (ponieważ cały obszar pod krzywą wynosi 1, a obszar na prawo od 0 wynosi 0,5). Podobnie, obszar dwóch ogonów, który jest sumą obszarów na prawo od 1,96 i na lewo od -1,96, wynosi dwa razy 0,025, czyli 0,05.
Jak to wszystko pomaga nam wnioskować statystycznie o populacjach, takich jak ta w naszym przykładzie cen domów? Podstawową ideą jest to, że dopasowujemy model rozkładu normalnego do naszej próbki danych, a następnie używamy tego modelu do wnioskowania o odpowiedniej populacji. Na przykład, możemy użyć obliczeń prawdopodobieństwa dla rozkładu normalnego (jak pokazano na rysunku powyżej), aby dokonać stwierdzeń prawdopodobieństwa o populacji modelowanej przy użyciu tego rozkładu normalnego – pokażemy dokładnie jak to zrobić w sekcji 1.3. Zanim jednak to zrobimy, zatrzymamy się, aby rozważyć pewien aspekt tej sekwencji wnioskowania, który może zadecydować o powodzeniu lub niepowodzeniu procesu. Czy model zapewnia wystarczająco bliskie przybliżenie do wzorca wartości z próby, abyśmy mogli być pewni, że model odpowiednio reprezentuje wartości populacji? Im lepsze przybliżenie, tym bardziej wiarygodne będą nasze stwierdzenia wnioskowania.
Wcześniej widzieliśmy jak krzywa gęstości może być pomyślana jako histogram z bardzo dużą próbką. Tak więc jednym ze sposobów oceny, czy nasza populacja podąża za modelem rozkładu normalnego, jest skonstruowanie histogramu z naszych danych z próbki i wizualne określenie, czy „wygląda normalnie”, to znaczy w przybliżeniu symetrycznie i w kształcie dzwonu. Jest to nieco subiektywna decyzja, ale z doświadczeniem powinniśmy zauważyć, że łatwiej jest odróżnić histogramy wyraźnie nienormalne od tych, które są w miarę normalne. Na przykład, podczas gdy histogram powyżej wyraźnie wygląda jak normalna krzywa gęstości, normalność histogramu 30 przykładowych cen sprzedaży w sekcji 1.1 jest mniej pewna. Rozsądny wniosek w tym przypadku byłby taki, że podczas gdy ten przykładowy histogram nie jest idealnie symetryczny i w kształcie dzwonu, jest wystarczająco blisko, że odpowiadający mu (hipotetyczny) histogram populacji mógłby być normalny.
Alternatywnym sposobem oceny normalności jest skonstruowanie wykresu QQ (quantile-quantile plot), znanego również jako normalny wykres prawdopodobieństwa, jak pokazano tutaj dla danych o cenach domów:
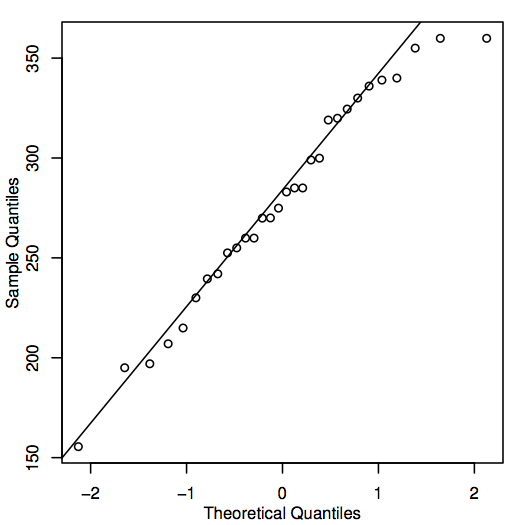
Jeśli punkty na wykresie QQ leżą blisko linii ukośnej, to odpowiadające im wartości populacji mogą być normalne. Jeśli punkty leżą daleko od linii, to normalność jest wątpliwa. Ponownie, jest to nieco subiektywna decyzja, która staje się łatwiejsza do podjęcia z doświadczeniem. W tym przypadku, biorąc pod uwagę dość mały rozmiar próbki, punkty są prawdopodobnie wystarczająco blisko linii, aby można było wyciągnąć wniosek, że wartości populacji mogą być normalne.
Istnieją również różne ilościowe metody oceny normalności – patrz rozdział 6.3.
.