W tym artykule wyjaśnię, w jaki sposób konwolucje 2D są implementowane jako mnożenie macierzy. Wyjaśnienie to jest oparte na notatkach z kursu CS231n Convolutional Neural Networks for Visual Recognition (Moduł 2). Zakładam, że czytelnik jest zaznajomiony z pojęciem operacji konwolucji w kontekście głębokiej sieci neuronowej. Jeśli nie, to w tym repo znajduje się raport i doskonałe animacje wyjaśniające czym są konwolucje. Kod do odtworzenia obliczeń w tym artykule można pobrać tutaj.
Mały przykład
Załóżmy, że mamy jednokanałowy obraz 4 x 4, X, a jego wartości pikseli są następujące:

Przypuśćmy dalej, że definiujemy konwolucję 2D o następujących właściwościach:

To oznacza, że będzie 9 łat obrazu 2 x 2, które będą elementowo mnożone przez macierz W, tak jak:

Te plamy obrazu mogą być reprezentowane jako 4-wymiarowe wektory kolumnowe i konkatenowane w celu utworzenia pojedynczej macierzy 4 x 9, P, jak poniżej:

Zauważ, że i-ta kolumna macierzy P jest w rzeczywistości i-tą łatą obrazu w postaci wektora kolumnowego.
Macierz wag dla warstwy konwolucji, W, może być spłaszczona do 4-wymiarowego wektora rzędów, K, w ten sposób:
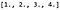
Aby wykonać konwolucję, najpierw mnożymy macierz K przez P, aby otrzymać 9-wymiarowy wektor rzędowy (macierz 1 x 9), co daje nam:

Następnie przekształcamy wynik K P do właściwego kształtu, którym jest macierz 3 x 3 x 1 (wymiar kanału ostatni). Wymiar kanału jest 1 ponieważ filtry wyjściowe ustawiliśmy na 1. Wysokość i szerokość jest 3 ponieważ zgodnie z notatkami CS231n:

To oznacza, że wynikiem konwolucji jest:
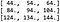
Co sprawdza się, jeśli wykonamy konwolucję przy użyciu wbudowanych funkcji PyTorcha (szczegóły w kodzie towarzyszącym temu artykułowi).
Większy przykład
Przykład w poprzedniej sekcji zakłada pojedynczy obraz, a kanały wyjściowe konwolucji mają wartość 1. Co by się zmieniło, gdybyśmy rozluźnili te założenia?
Załóżmy, że naszym wejściem do konwolucji jest obraz 4 x 4 z 3 kanałami o następujących wartościach pikseli:

Jeśli chodzi o naszą konwolucję, ustawimy ją tak, aby miała takie same właściwości jak w poprzedniej sekcji, z wyjątkiem tego, że jej filtry wyjściowe wynoszą 2. Oznacza to, że początkowa macierz wag, W, musi mieć kształt (2, 2, 2, 3) tj. (filtry wyjściowe, wysokość jądra, szerokość jądra, kanały obrazu wejściowego). Ustawmy W na następujące wartości:

Zauważ, że każdy z filtrów wyjściowych będzie miał swoje własne jądro (dlatego w tym przykładzie mamy 2 jądra) i kanał każdego jądra jest 3 (ponieważ obraz wejściowy ma 3 kanały).
Ponieważ nadal konwulgujemy jądro 2 x 2 na obrazie 4 x 4 z 0 zero-padding i stride 1, liczba łat obrazu jest nadal 9. Jednakże, macierz łat obrazu, P, będzie inna. Dokładniej, i-ta kolumna P będzie konkatenacją wartości 1-go, 2-go i 3-go kanału (jako wektor kolumnowy) odpowiadających i-tej plamie obrazu. P będzie teraz macierzą 12 x 9. Rzędów jest 12, ponieważ każda łata obrazu ma 3 kanały, a każdy kanał ma 4 elementy, ponieważ ustawiliśmy rozmiar jądra na 2 x 2. Oto, jak wygląda P:

Tak jak w przypadku W, każde jądro zostanie spłaszczone do wektora rzędów i połączone rzędami w celu utworzenia macierzy 2 x 12, K. I-ty rząd K jest konkatenacją wartości 1, 2 i 3 kanału (w formie wektora rzędów) odpowiadających i-temu jądru. Oto jak będzie wyglądała macierz K:

Teraz pozostaje tylko wykonać mnożenie macierzy K P i przekształcić ją do właściwego kształtu. Prawidłowym kształtem jest macierz 3 x 3 x 2 (wymiar kanału ostatni). Oto wynik mnożenia:

A oto wynik po przekształceniu do macierzy 3 x 3 x 2:

Co znów sprawdza się, jeśli mamy wykonać konwolucję przy użyciu wbudowanych funkcji PyTorcha (szczegóły w kodzie towarzyszącym temu artykułowi).
So What?
Dlaczego powinniśmy dbać o wyrażanie konwolucji 2D w kategoriach mnożenia macierzy? Oprócz posiadania wydajnej implementacji nadającej się do uruchomienia na procesorze graficznym, znajomość tego podejścia pozwoli nam zrozumieć zachowanie głębokiej konwolutnej sieci neuronowej. Dla przykładu, He et. al. (2015) wyrazili konwolucje 2D w kategoriach mnożenia macierzy, co pozwoliło im zastosować właściwości losowych macierzy/wektorów, aby argumentować za lepszą procedurą inicjalizacji wag.
Wniosek
W tym artykule wyjaśniłem, jak wykonać konwolucje 2D przy użyciu mnożenia macierzy, przechodząc przez dwa małe przykłady. Mam nadzieję, że to wystarczy, aby uogólnić do dowolnych wymiarów obrazu wejściowego i właściwości konwolucji. Daj mi znać w komentarzach, jeśli coś jest niejasne.
1D Convolution
Metoda opisana w tym artykule generalizuje również do 1D convolutions.
Na przykład załóżmy, że twoje dane wejściowe to 3-kanałowy wektor 12-wymiarowy taki jak:

Jeśli ustawimy naszą konwolucję 1D tak, aby miała następujące parametry:
- rozmiar jądra: 1 x 4
- kanały wyjściowe: 2
- stride: 2
- padding: 0
- bias: 0
Wtedy parametry w operacji konwolucji, W, będą tensorem o kształcie (2 , 3, 1, 4). Ustalmy, że W będzie miał następujące wartości:

W oparciu o parametry operacji konwolucji, macierz „obrazowych” łat P, będzie miała kształt (12, 5) (5 łat obrazowych, gdzie każda z łat obrazowych jest wektorem 12-D, gdyż łata ma 4 elementy w 3 kanałach) i będzie wyglądać następująco:

Następnie spłaszczamy W, aby uzyskać K, która ma kształt (2, 12), ponieważ istnieją 2 jądra, a każde jądro ma 12 elementów. Oto jak wygląda K:

Teraz możemy pomnożyć K przez P co daje:

Na koniec przekształcamy K P do właściwego kształtu, którym zgodnie ze wzorem jest „obraz” o kształcie (1, 5). Oznacza to, że wynikiem tej konwolucji jest tensor o kształcie (2, 1, 5), ponieważ kanały wyjściowe ustawiliśmy na 2. Tak wygląda wynik końcowy:

Co zgodnie z oczekiwaniami sprawdza się, gdybyśmy mieli wykonać konwolucję za pomocą wbudowanych funkcji PyTorcha.
.