Definicja

Wielomian na zmiennej x to funkcja, którą można zapisać w postaci,

gdzie an, an-1 , …, a2, a1, a0 są stałymi. Wyraz zawierający największą potęgę x (tzn. anxn) nazywamy wyrazem wiodącym, a an nazywamy współczynnikiem wiodącym. Stopień wielomianu to potęga x w pierwszorzędnym członie. Widzieliśmy już wielomiany stopnia 0, 1 i 2, które były odpowiednio funkcjami stałymi, liniowymi i kwadratowymi. Wielomiany stopnia 3, 4 i 5 również mają specjalne nazwy: funkcje sześcienne, kwartowe i kwintowe. Wielomiany stopnia n > 5 nazywane są wielomianami n-tego stopnia. Nazwy różnych funkcji wielomianowych są podsumowane w poniższej tabeli.

.

Stopień wielomianu	Nazwa funkcji
0	Stała funkcji
1	Funkcja liniowa
2	Funkcja kwadratowa
3	Funkcja sześcienna
4	Funkcja kwarcowa
5	Funkcja kwintyczna
n (gdzie n > 5)	wielomian n-tego stopnia

Niektóre przykłady wielomianów obejmują:

Zachowanie graniczne wielomianów

Zachowanie graniczne funkcji opisuje, co dzieje się z funkcją, gdy x → ±∞. Stopień wielomianu i znak jego wiodącego współczynnika dyktuje jego graniczne zachowanie. W szczególności

Wyniki te są podsumowane w poniższej tabeli.

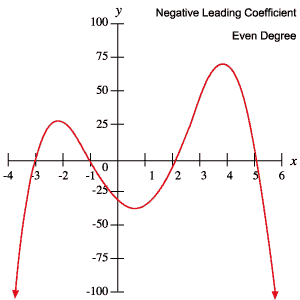
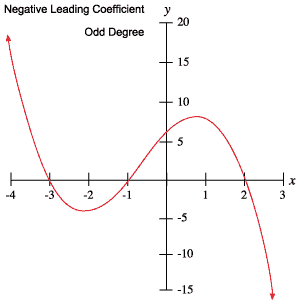
Możesz użyć tych informacji, aby określić, czy wielomian ma stopień nieparzysty czy parzysty i czy współczynnik wiodący jest dodatni czy ujemny, po prostu sprawdzając jego wykres.

Następujące wykresy wielomianów są przykładem każdego z zachowań przedstawionych w powyższej tabeli.

Podstawy i punkty zwrotne

Stopień wielomianu mówi o nim jeszcze więcej niż zachowanie ograniczające. Konkretnie, wielomian n-tego stopnia może mieć co najwyżej n prawdziwych korzeni (punktów przecięcia x lub zer) licząc mnożniki. Na przykład, załóżmy, że patrzymy na wielomian szóstego stopnia, który ma 4 różne korzenie. Jeśli dwa z tych czterech korzeni mają krotność 2, a pozostałe 2 mają krotność 1, to wiemy, że nie ma innych korzeni, ponieważ uwzględniliśmy wszystkie 6 korzeni. To dlatego, że korzenie o krotności dwa (znane również jako podwójne korzenie) są liczone jako dwa korzenie.

Uważaj, że wielomian n-tego stopnia nie musi mieć n rzeczywistych korzeni – może mieć mniej, ponieważ ma urojone korzenie. Zauważ, że wielomian stopnia nieparzystego musi mieć co najmniej jeden pierwiastek rzeczywisty, ponieważ funkcja zbliża się do – ∞ na jednym końcu i + ∞ na drugim; funkcja ciągła, która przechodzi od ujemnego do dodatniego, musi przeciąć oś x gdzieś pomiędzy. Ponadto wielomian n-tego stopnia może mieć co najwyżej n – 1 punktów zwrotnych. Punktem zwrotnym jest punkt, w którym funkcja zmienia się z rosnącej na malejącą lub z malejącej na rosnącą, jak widać na poniższym rysunku. Ponownie, wielomian n-tego stopnia nie musi mieć n – 1 punktów zwrotnych, może mieć ich mniej.

Uwaga

Ważne jest, aby zdać sobie sprawę z różnicy między funkcjami parzystymi i nieparzystymi oraz wielomianami parzystego i nieparzystego stopnia. Każda funkcja, f(x), jest albo parzysta, jeśli,

f(-x) = x,

dla wszystkich x w dziedzinie f(x), albo nieparzysta, jeśli,

f(-x) = -x,

dla wszystkich x w dziedzinie f(x), albo ani parzysta, ani nieparzysta, jeśli żadne z powyższych stwierdzeń nie jest prawdziwe.

Mówi się, że wielomian k-tego stopnia, p(x), ma stopień parzysty, jeśli k jest liczbą parzystą i stopień nieparzysty, jeśli k jest liczbą nieparzystą. Pamiętajmy, że nawet jeśli p(x) ma stopień parzysty, to niekoniecznie jest funkcją parzystą. Podobnie, jeśli p(x) ma stopień nieparzysty, to niekoniecznie jest funkcją nieparzystą.

Pojęć parzystości i nieparzystości używamy również do opisu pierwiastków wielomianów. W szczególności, wielomian p(x) ma pierwiastek x = a o k krotności (tzn. x = a jest pierwiastkiem powtórzonym k razy), jeśli (x – a)k jest współczynnikiem p(x). Mówimy, że x = a ma parzystą krotność, jeśli k jest liczbą parzystą i nieparzystą krotność, jeśli k jest liczbą nieparzystą.

Domena i zakres

Wszystkie wielomiany mają tę samą dziedzinę, która składa się ze wszystkich liczb rzeczywistych. Zakres wielomianów stopnia nieparzystego również składa się z wszystkich liczb rzeczywistych. Zakres wielomianów stopnia parzystego jest nieco bardziej skomplikowany i nie możemy jednoznacznie określić zakresu wszystkich wielomianów stopnia parzystego. Jeśli współczynnik wiodący jest dodatni, to funkcja będzie się rozciągać do + ∞; natomiast jeśli współczynnik wiodący jest ujemny, to będzie się rozciągać do – ∞. Oznacza to, że wielomiany stopnia parzystego o dodatnim współczynniku wiodącym mają przedział, w którym ymax oznacza maksimum globalne, jakie osiąga funkcja. W ogólności nie da się analitycznie wyznaczyć maksimów i minimów wielomianów.

*****

W następnym rozdziale poznasz dzielenie wielomianów, technikę używaną do znajdowania pierwiastków funkcji wielomianowych.

Działanie wielomianów