Faza oscylacji lub fali to ułamek pełnego cyklu odpowiadający przesunięciu w przemieszczeniu względem określonego punktu odniesienia w czasie t = 0. Faza jest pojęciem z dziedziny częstotliwości lub z dziedziny transformaty Fouriera i jako taka może być łatwo zrozumiana w kategoriach prostego ruchu harmonicznego. Ta sama koncepcja odnosi się do ruchu falowego, postrzeganego albo w punkcie przestrzeni w przedziale czasu, albo w całym przedziale przestrzeni w danym momencie czasu. Ruch harmoniczny prosty to przemieszczenie, które zmienia się cyklicznie, jak pokazano poniżej:
File:Simple harmonic motion.png
i opisany wzorem:

gdzie A jest amplitudą oscylacji, f jest częstotliwością, t jest czasem, który upłynął, a 

Można zauważyć dwie potencjalne niejednoznaczności:
- Jedną z nich jest to, że początkowe przemieszczenie
jest inne niż funkcja sinus, a jednak wydaje się, że mają one tę samą „fazę”.
- Zmienna w czasie wartość kąta
lub jego wartość modulo
, jest również powszechnie nazywana „fazą”. Wówczas nie jest to warunek początkowy, a raczej stale zmieniający się stan.
Termin faza chwilowa jest używany do odróżnienia kąta zmiennego w czasie od warunku początkowego. Ma on również formalną definicję, która ma zastosowanie do bardziej ogólnych funkcji i jednoznacznie określa fazę początkową funkcji w chwili t=0. Tzn. sinus i cosinus z natury mają różne fazy początkowe. Jeśli nie jest wyraźnie powiedziane inaczej, cosinus powinien być generalnie wnioskowany. (patrz też fazor)
Przesunięcie fazowe
Ilustracja przesunięcia fazowego. Oś pozioma reprezentuje kąt (fazę), który rośnie z czasem.


Dla nieskończenie długich sinusoid, zmiana 


 |
 |
{displaystyle =Acdot \sin(2\pi ft-{begin{matrix}{\frac {{2}}}\end{matrix}}+theta ),\którego „fazą” jest teraz  Została ona przesunięta o Została ona przesunięta o  . .
Różnica fazFale w fazie Out-of-phase waves Lewa: część rzeczywista fali płaskiej poruszającej się z góry na dół. Po prawej: ta sama fala po tym, jak jej środkowa część uległa przesunięciu fazowemu, na przykład przechodząc przez szkło o innej grubości niż pozostałe części. (Ilustracja po prawej stronie pomija efekt dyfrakcji, której działanie wzrasta przy dużych odległościach). Dwa oscylatory, które mają tę samą częstotliwość i różne fazy, mają różnicę faz i mówi się, że oscylatory są ze sobą poza fazą. Wartość, o jaką takie oscylatory są ze sobą poza fazą, można wyrazić w stopniach od 0° do 360° lub w radianach od 0 do 2π. Jeżeli różnica faz wynosi 180 stopni (π radianów), wówczas mówi się, że dwa oscylatory są w antyfazie. Jeśli dwie oddziałujące na siebie fale spotkają się w punkcie, w którym są w antyfazie, wówczas wystąpi interferencja destrukcyjna. Często zdarza się, że fale elektromagnetyczne (światło, RF), akustyczne (dźwięk) lub inne nakładają się na siebie w medium transmisyjnym. Kiedy tak się dzieje, różnica faz decyduje o tym, czy fale wzmacniają się czy osłabiają. Całkowite anulowanie jest możliwe dla fal o równych amplitudach. Czas jest czasami używany (zamiast kąta) do wyrażenia pozycji w cyklu oscylacji.
Składowe in-phase i quadrature (I&Q)Pojęcie in-phase występuje również w kontekście sygnałów komunikacyjnych: i: gdzie {displaystyle I(t)\ {\stackrel {\i0}. }{=}} A(t)}
Koherencja fazowaKoherencja jest cechą fali polegającą na wykazywaniu dobrze zdefiniowanej zależności fazowej w różnych regionach jej dziedziny definicji. W fizyce, mechanika kwantowa przypisuje fale do obiektów fizycznych. Funkcja falowa jest złożona, a ponieważ jej moduł kwadratowy jest związany z prawdopodobieństwem zaobserwowania obiektu, złożony charakter funkcji falowej jest związany z fazą. Ponieważ złożona algebra jest odpowiedzialna za uderzający efekt interferencji w mechanice kwantowej, faza cząstek jest zatem ostatecznie związana z ich kwantowym zachowaniem. . |


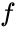 reprezentuje częstotliwość nośną, i
reprezentuje częstotliwość nośną, i i
i  reprezentują możliwą modulację czystej fali nośnej, np:
reprezentują możliwą modulację czystej fali nośnej, np:  Modulacja zmienia pierwotną
Modulacja zmienia pierwotną  składową nośnej i tworzy (nową)
składową nośnej i tworzy (nową) 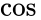 składową, jak pokazano powyżej. Składowa, która jest w fazie z oryginalnym nośnikiem, jest określana jako składowa w fazie. Druga składowa, która jest zawsze 90° (
składową, jak pokazano powyżej. Składowa, która jest w fazie z oryginalnym nośnikiem, jest określana jako składowa w fazie. Druga składowa, która jest zawsze 90° (