Klasyfikacja jest nadzorowanym podejściem do uczenia maszynowego, w którym algorytm uczy się na podstawie dostarczonych mu danych wejściowych – a następnie wykorzystuje to uczenie do klasyfikowania nowych obserwacji.

Innymi słowy, zbiór danych szkoleniowych jest wykorzystywany do uzyskania lepszych warunków brzegowych, które mogą być użyte do określenia każdej klasy docelowej; po określeniu takich warunków brzegowych, następnym zadaniem jest przewidywanie klasy docelowej.

Jednym z pierwszych popularnych algorytmów klasyfikacji w uczeniu maszynowym był Naive Bayes, klasyfikator probabilistyczny zainspirowany twierdzeniem Bayesa (które pozwala nam na rozumowe wnioskowanie o zdarzeniach zachodzących w świecie rzeczywistym na podstawie wcześniejszej wiedzy o obserwacjach, które mogą to sugerować). Nazwa („Naive”) pochodzi od faktu, że algorytm zakłada, że atrybuty są warunkowo niezależne.

Algorytm jest prosty w implementacji i zwykle stanowi rozsądną metodę rozpoczęcia wysiłków klasyfikacyjnych. Może on łatwo skalować się do większych zbiorów danych (zajmuje liniowy czas w porównaniu z iteracyjnym przybliżeniem, stosowanym w wielu innych typach klasyfikatorów, co jest bardziej kosztowne pod względem zasobów obliczeniowych) i wymaga niewielkiej ilości danych treningowych.

Jednakże Naive Bayes może cierpieć z powodu problemu znanego jako „problem zerowego prawdopodobieństwa”, gdy prawdopodobieństwo warunkowe wynosi zero dla danego atrybutu, nie zapewniając prawidłowej prognozy. Jednym z rozwiązań jest zastosowanie procedury wygładzania (np. metoda Laplace’a).

P(c|x) jest prawdopodobieństwem potomnym klasy (c, cel) biorąc pod uwagę predyktor (x, atrybuty). P(c) jest wcześniejszym prawdopodobieństwem klasy. P(x|c) jest prawdopodobieństwem, które jest prawdopodobieństwem predyktora danego przez klasę, a P(x) jest wcześniejszym prawdopodobieństwem predyktora.

Pierwszy krok algorytmu polega na obliczeniu wcześniejszego prawdopodobieństwa dla danych etykiet klas. Następnie znalezienie prawdopodobieństwa prawdopodobieństwa z każdym atrybutem, dla każdej klasy. Następnie umieszczenie tych wartości we wzorze Bayesa & obliczenie prawdopodobieństwa potomnego, a następnie sprawdzenie, która klasa ma wyższe prawdopodobieństwo, biorąc pod uwagę, że dane wejściowe należą do klasy o wyższym prawdopodobieństwie.

Wdrożenie Naive Bayes w Pythonie jest dość proste poprzez wykorzystanie biblioteki scikit-learn. Istnieją właściwie trzy typy modelu Naive Bayes w ramach biblioteki scikit-learn: (a) typu Gaussian (zakłada, że cechy podążają za dzwonowatym, normalnym rozkładem), (b) wielomianowy (używany dla dyskretnych zliczeń, w sensie ilości razy wynik jest obserwowany na przestrzeni x prób), oraz (c] Bernoulli (przydatny dla binarnych wektorów cech; popularnym przypadkiem użycia jest klasyfikacja tekstu).

Innym popularnym mechanizmem jest drzewo decyzyjne. Biorąc pod uwagę dane atrybutów wraz z ich klasami, drzewo tworzy sekwencję reguł, które mogą być użyte do klasyfikacji danych. Algorytm dzieli próbkę na dwa lub więcej jednorodnych zbiorów (liści) na podstawie najbardziej znaczących różnic w zmiennych wejściowych. Aby wybrać wyróżnik (predyktor), algorytm bierze pod uwagę wszystkie cechy i dokonuje na nich podziału binarnego (dla danych kategorycznych, podział według kota; dla ciągłych, wybierz próg odcięcia). Następnie wybierze cechę o najmniejszym koszcie (tj. najwyższej dokładności), powtarzając rekurencyjnie, aż do pomyślnego podziału danych we wszystkich liściach (lub osiągnięcia maksymalnej głębokości).

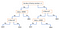
Drzewa decyzyjne są generalnie łatwe do zrozumienia i wizualizacji, wymagając niewielkiego przygotowania danych. Metoda ta może również obsługiwać zarówno dane numeryczne, jak i kategoryczne. Z drugiej strony, złożone drzewa nie generalizują dobrze („przepasowanie”), a drzewa decyzyjne mogą być nieco niestabilne, ponieważ małe zmiany w danych mogą spowodować wygenerowanie zupełnie innego drzewa.

Metodą klasyfikacji, która wywodzi się z drzew decyzyjnych jest Random Forest, zasadniczo „meta-estymator”, który dopasowuje pewną liczbę drzew decyzyjnych do różnych podpróbek zbiorów danych i wykorzystuje średnią w celu poprawy dokładności predykcyjnej modelu i kontroluje przepasowanie. Rozmiar podpróbki jest taki sam jak rozmiar oryginalnej próbki wejściowej – ale próbki są losowane z zastąpieniem.

Lasy losowe mają tendencję do wykazywania wyższego stopnia odporności na przepełnienie (>odporność na szum w danych), z wydajnym czasem wykonania nawet w większych zbiorach danych. Są one jednak bardziej wrażliwe na niezrównoważone zbiory danych, są również nieco bardziej skomplikowane w interpretacji i wymagają więcej zasobów obliczeniowych.

Innym popularnym klasyfikatorem w ML jest regresja logistyczna – gdzie prawdopodobieństwa opisujące możliwe wyniki pojedynczej próby są modelowane za pomocą funkcji logistycznej (metoda klasyfikacji pomimo nazwy):

Tutaj jak wygląda równanie logistyczne:

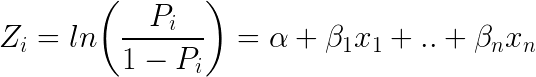
Odejmując e (wykładnik) po obu stronach równania otrzymujemy:

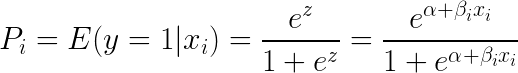
Regresja logistyczna jest najbardziej przydatna do zrozumienia wpływu kilku zmiennych niezależnych na pojedynczą zmienną wynikową. Skupia się ona na klasyfikacji binarnej (dla problemów z wieloma klasami używamy rozszerzeń regresji logistycznej, takich jak wielomianowa i porządkowa regresja logistyczna). Regresja logistyczna jest popularna w przypadkach użycia takich jak analiza kredytowa i skłonność do odpowiedzi/kupna.

Ostatni, ale nie mniej ważny, kNN (dla „k Nearest Neighbors”) jest również często używany do problemów z klasyfikacją. kNN jest prostym algorytmem, który przechowuje wszystkie dostępne przypadki i klasyfikuje nowe przypadki w oparciu o miarę podobieństwa (np. funkcje odległości). Był on stosowany w estymacji statystycznej i rozpoznawaniu wzorców już na początku lat 70-tych jako technika nieparametryczna:

.