Acta Cryst. (1992). A48, 727-732![]()
Final report of the International Union of Crystallography Ad-Hoc Committee on the nomenclature of symmetry*
By P. M. DE WOLFF (Chairman), Meermanstraat 126, 2614 AM Delft, The Netherlands,
Y. BILLIET, Ecole Nationale d’Ingénieurs, BPW 3038 Sfax, Tunesië,
J. D. H. DONNAY, Department of Geological Sciences, McGill University, 3450 University Street, Montreal, Canada H3A 2A7,
W. FISCHER, Institut für Mineralogie, Petrologie und Kristallographie der Phillips-Universität, Lahnberge, D-3550 Marburg (Lahn), Germany,
R. B. GALIULIN, Institute of Crystallography, Academy of Sciences of Russia, Leninsky Prospekt 59, Moscow 117333, Russia,
A. M. GLAZER, Clarendon Laboratory, University of Oxford, Parks Road, Oxford OX1 3PU England,
TH. HAHN, Institut für Kristallographie, RWTH, Templergraben 55, D-5100 Aachen, Germany,
MARJORIE SENECHAL, Department of Mathematics, Smith College, Northampton, MA 01063, USA,
D. P. SHOEMAKER, Chemistry Department, Oregon State University, OR 97331, USA,
H. WONDRATSCHEK, Institut für Kristallographie, Universität Karlsruhe, Kaiserstrasse 12, D-7500 Karlsruhe 1, Germany,
A. J. C. WILSON (ex officio, IUCr Commission on International Tables), Crystallographic Data Centre, University Chemistry Laboratory, Lensfield Road, Cambridge CB2 1EW, England
AND S. C. ABRAHAMS (ex officio, IUCr Commission on Crystallographic Nomenclature), Department of Physics, Southern Oregon State College, 1250 Siskiyou Boulevard, Ashland, OR 97520-5047, USA
(Received 7 November 1991; accepted 9 March 1992)
* Mianowany 14 listopada 1984, zmieniony 10 sierpnia 1987 na podstawie podstawowych zasad określonych w Acta Cryst. (1979), A35, 1072. Final Report accepted 23 December 1991 by the IUCr Commission on Crystallographic Nomenclature and 9 March 1992 by the Executive Committee.
Abstract
New or redefined printed symbols are proposed in the light of the recently accepted redefinition of symmetry elements . W szczególności litera e obejmuje pewne płaszczyzny ślizgowe, które do tej pory nie miały unikalnego symbolu, takie jak płaszczyzny określane jako „albo a albo b”. Zaleca się stosowanie litery e w symbolu Hermanna-Mauguina pięciu różnych grup przestrzeni. Dla płaszczyzn e rzutowanych w kierunku równoległym do płaszczyzny proponuje się symbol graficzny, który usuwa niejednoznaczność ich obecnego oznaczenia. Proponuje się literę k dla nowo zdefiniowanej klasy płaszczyzn ślizgowych, które do tej pory nie miały określonego symbolu. Symbole dla operacji symetrii wprowadzone w opisach grup przestrzeni w International Tables for Crystallography (1989), Vol. A (Dordrecht: Kluwer Academic Publishers) są zalecane do ogólnego stosowania, z modyfikacjami tylko dla operacji odbicia ślizgowego.
Wprowadzenie
Komitet ad-hoc powołany w 1980 roku do rozważenia „problemów nomenklatury dotyczących operacji symetrii i elementów symetrii w grupach przestrzennych” wydał dwa Raporty zatytułowane Nomenclature for Crystal Families, Bravais-Lattice Types and Arithmetic Classes (de Wolff et al., 1985) oraz Definition of Symmetry Elements in Space Groups and Point Groups (de Wolff et al., 1989). Jak zauważono w raporcie z 1989 roku, jedynym nierozwiązanym problemem dotyczącym operacji symetrii jest wybór odpowiednich symboli, ponieważ pojęcie jest jasne. Tymczasowa notacja została przyjęta w International Tables for Crystallography (1983, 1989), zwana dalej ITA83.
Symbole drukowane dla elementów symetrii
Definicja elementów symetrii podana w Raporcie 1989 (de Wolff et al.) będzie stosowana w całym niniejszym Raporcie. Tutaj powtarzamy jej istotę:
Dla każdej danej operacji symetrii zdefiniowany jest jej element geometryczny (płaszczyzna, punkt i/lub linia). Element symetrii jest połączeniem elementu geometrycznego jednej z operacji symetrii w danej grupie przestrzeni ze zbiorem (zwanym „zbiorem elementów”) wszystkich operacji symetrii w tej grupie przestrzeni, które dzielą ten element geometryczny.
Szczegółowe definicje elementów geometrycznych i opisy wynikających z nich elementów symetrii, jak również ich symbole są podane w tabelach 1 i 2. (Są one identyczne z tabelami 1 i 2 w Sprawozdaniu z 1989 r., z wyjątkiem płaszczyzn ślizgowych, i są tu powtórzone dla kompletności, patrz poniżej). Każdy element symetrii jest reprezentowany przez symbol składający się z dwóch znaków. Pierwszy znak jest wielką literą E dla wszystkich elementów symetrii. Służy on do pokazania, że symbol odnosi się do elementu symetrii, a nie na przykład do operacji symetrii. Jeżeli wynika to już z kontekstu, to E może być pominięte, np. „oś 2” zamiast „oś E2”.
| Operacja symetrii | Element geometryczny | Parametry dodatkowe |
|---|---|---|
| Tożsamość | Niewymagana | Brak |
| Translacja | Niewymagana | Wektor |
| Odbicie w płaszczyźnie A | Płaszczyzna A | Brak |
| Odbicie w ślizgu = odbicie w płaszczyźnie A i translacja |
Płaszczyzna A | Wektor poślizgu |
| Rotacja względem prostej b | Linia b | Kąt i sens obrotu |
| Obrót śruby = obrót o prostą b i przesunięcie $ równoległe do b | Linia b | Kąt i sens śruby obrotu wektora $mathbf{u}$ |
| Rotinwersja = obrót o prostą b i inwersja przez punkt P na b | Linia b i punkt P na b | Kąt (nie równy |
| Odwrócenie przez punkt P | Punkt P | Brak |
Symbol Eg wymieniony w raporcie z 1989 roku może być użyty dla płaszczyzn ślizgowych, jeśli chce się tylko pokazać, że element symetrii jest płaszczyzną ślizgową. Jeżeli natomiast należy on do jednego ze specjalnych rodzajów, które od dawna są oznaczane odpowiednią literą (a, b, c, n lub d; por. ITA83), to litera ta zastępuje g w Eg.
| Nazwa elementu symetrii | Symbol | Element geometryczny | Operacja definiująca (d.o.) | Operacje w zbiorze elementów |
|---|---|---|---|---|
| Płaszczyzna lustrzana | Em | Płaszczyzna A | Odbicie w A | D.o. i jej koplanarne odpowiedniki* |
| Płaszczyzna poślizgu | Eg |
Płaszczyzna A | Odbicie w A, 2v (nie v) translacja kratowa | D.o. i jej koplanarne odpowiedniki* |
| Oś obrotu | En | Linia b | Obrót wokół b, kąt |
1-sza, |
| Oś śruby | Enj | Linia b | Obrót śruby wokół b, kąt translacja wzdłuż b, śruba prawoskrętna; n = 2, 3, 4 lub 6, |
1., |
| Osie rotacji | Linia b i punkt P na b | Rotinwersja: obrót wokół b, kąt |
D.o. i jego odwrotność | |
| Centrum | Punkt P | Inwersja przez P | D.o. only |
* Czyli wszystkie odbicia ślizgowe z tą samą płaszczyzną odbicia, z wektorami ślizgowymi różniącymi się od wektora d.o. (przyjmowanego jako zero dla odbicia) o wektor translacji kraty.![]() Czyli wszystkie obroty i obroty śrubowe o tej samej osi b, tym samym kącie i sensie obrotu oraz tym samym wektorze śrubowym $mathbf{u}$ (zerowym dla obrotu) aż do wektora translacji kratowej.
Czyli wszystkie obroty i obroty śrubowe o tej samej osi b, tym samym kącie i sensie obrotu oraz tym samym wektorze śrubowym $mathbf{u}$ (zerowym dla obrotu) aż do wektora translacji kratowej.![]() W Eg, g jest zastępowane przez a, b, c, n, d, e lub k dla określonych rodzajów płaszczyzn ślizgowych, por. §2.
W Eg, g jest zastępowane przez a, b, c, n, d, e lub k dla określonych rodzajów płaszczyzn ślizgowych, por. §2.
Na ważny nowy aspekt symboli takich jak Eb można jednak zwrócić uwagę. Według ITA83, oznaczanie płaszczyzny przez b oznaczało jedynie, że odbicie ślizgowe w płaszczyźnie ze składową ślizgową b/2 wzdłuż osi b jest operacją symetrii. Definicja ta z pewnością ma zastosowanie do sytuacji przedstawionej na Rys. 1.
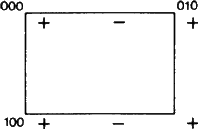
Rys. 1 jest zaadaptowany, podobnie jak rys. 2 i 3, z zestawu podobnych rysunków zaprojektowanych przez członka Komitetu Ad-hoc W. Fischera jako spis wszystkich typów płaszczyzn ślizgowych. Chociaż zestaw ten został przedstawiony Komitetowi w 1980 r., na długo przed ukazaniem się Raportu z 1989 r., każdy z jego rysunków przedstawia dokładnie „zestaw elementów” samolotu ślizgowego zdefiniowany w tymże Raporcie (por. powyższe streszczenie). W przypadku płaszczyzny poślizgu zbiór elementów składa się ze wszystkich odbić poślizgu, których wspólnym elementem geometrycznym jest płaszczyzna. Ich działanie jest pokazane w rzucie na tę płaszczyznę. Od pozycji wyjściowej dowolnego znaku +, każdy znak – wynika z jednego z odbić ślizgowych tego zbioru. Wszystkie one są pokazane w elementarnej siatce powstałego dwuwymiarowego układu okresowego znaków + i -.
Będziemy często odnosić się do siatki N utworzonej przez wszystkie translacje równoległe do płaszczyzny; siatka ta jest łatwo wizualizowana przez patrzenie tylko na znaki +. Wektory te należy wyraźnie odróżnić od wektorów łączących znak + z dowolnym znakiem -, z których każdy jest wektorem odbicia ślizgowego należącym do zbioru elementów.
Nowy aspekt wynika z tego, że w niektórych przypadkach, zgodnie z definicją ITA83, płaszczyzna b-ślizgowa jest również płaszczyzną a-ślizgową; patrz Rys. 2. Oczywiście dzieje się tak tylko wtedy, gdy siatka N jest ortogonalnie centrowana, ponieważ wtedy a-ślizg może być zmieniony na b-ślizg (i odwrotnie) przez dodanie przesunięcia centrującego. Dotychczasowa praktyka polegała na arbitralnym nazywaniu takiej płaszczyzny glejtu a lub b, co powodowało nieuzasadnioną tendencyjność i brak jednoznaczności tych symboli. Dlatego proponujemy, aby przypadek z rys. 2 objąć osobnym symbolem.
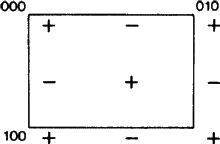
Zakres tego symbolu powinien być zatem rozszerzony na płaszczyzny ślizgowe w orientacji ukośnej, to znaczy równoległe tylko do jednej osi kryształu, pod warunkiem, że płaszczyzna ślizgowa ma wektor ślizgowy wzdłuż tej osi i że siatka N jest ortogonalnie centrowana. Dla takich płaszczyzn nie ma niejednoznaczności powyższego losowego wyboru a-b, ale rozszerzony zakres nowego symbolu jest zgodny z zakresem wszystkich istniejących symboli (mianowicie a, b, c, n i d). Każdy z nich jest stosowany dla płaszczyzny glejowej zarówno z jedną, jak i z dwoma osiami krystalicznymi w sieci N, por. Rys. 3.
Dla nowego symbolu proponuje się literę e. Tak więc Ee będzie dotyczyć płaszczyzn ślizgowych z ortogonalnymi siatkami centrującymi N i co najmniej jednym wektorem ślizgowym wzdłuż osi krystalicznej. Konieczne jest więc nowe kryterium, a mianowicie orientacja wektorów szybujących w stosunku do osi konwencjonalnych kryształu. Ponieważ te ostatnie leżą wzdłuż kierunków symetrii, a każda płaszczyzna glejtu jest równoległa do płaszczyzny lustrzanej kraty, nie dziwi fakt, że w N jest zawsze co najmniej jedna konwencjonalna oś kryształu, a jeśli jest tylko jedna taka oś, to prostopadle do niej jest zawsze inne przesunięcie w N.
Nowy symbol e, jak również stare symbole a, b, c, d, n zostaną teraz ponownie zdefiniowane pod względem tego nowego kryterium i typu Bravais sieci N. Ta sieć jest monokliniczna lub ortogonalna lub tetragonalna pierwotna (mp lub op lub tp) lub ortogonalna centrowana (oc). Tylko siatki N typu oc dopuszczają płaszczyznę ślizgową Ee. Symbol En stosuje się do siatek N typu Bravais mp lub op, natomiast Ed do siatek N typu oc. (Jak podaje przypis do Tabeli 1.3 w ITA83: „Płaszczyzny ślizgowe d występują tylko w ortorhombicznych grupach przestrzeni F, w tetragonalnych grupach przestrzeni I oraz w kubicznych grupach przestrzeni I i F. Występują one zawsze parami z naprzemiennymi wektorami ślizgowymi’). W przeciwieństwie jednak do płaszczyzn Ea, Eb, Ec i Ee, dla płaszczyzn En i Ed nie ma wektora glejtu ani równoległego, ani prostopadłego do osi umownej w N.
Wynikające stąd definicje płaszczyzn glejtu powyższych rodzajów zestawione są w wierszach (i) i (ii) Tabeli 3, a bardziej jednoznacznie na Rys. 3.
|
Symbol jest określany na podstawie dwóch kryteriów. Jednym kryterium jest typ Bravais’go (mp, op, tp lub oc) siatki N utworzonej przez translacje symetrii równoległe do rozpatrywanej płaszczyzny. Sieć ta zawiera zawsze co najmniej jedną konwencjonalną oś kryształu.* Drugie kryterium odnosi się do orientacji wektorów ślizgowych względem takich osi. |
||
| Liczba wektorów glejowych równoległych lub prostopadłych do osi krystalicznych w sieci N | Bravais typ sieci N | |
|---|---|---|
| m, op, tp | oc | |
| (i) Jedna lub dwie równoległe | Ec(Ea, Eb) | Ee |
| (ii) Żaden równoległy, żaden prostopadły | En | Ed |
| (iii) Żaden równoległy, jeden prostopadły | Ek | – |
* Zgodnie z definicją w ITA83, § 9.1; jednakże, dla grup przestrzeni romboedrycznych, używane są tu tylko osie heksagonalne.
Wszystkie pozostałe płaszczyzny ślizgowe były wcześniej bez określonego symbolu. Każda z nich ma orientację diagonalną (tylko jedna umowna oś kryształu w sieci N). Wśród refleksów ślizgowych w ich zbiorze elementów nie ma żadnego z wektorem ślizgowym wzdłuż tej osi. Jednak jeden wektor glejtu jest (przez symetrię) do niej prostopadły. Symbol wydaje się pożądany, więc ponownie proponujemy nową literę: k. Nowy symbol Ek jest krótko zdefiniowany w wierszu (iii) Tabeli 3 i jest w pełni zilustrowany w dolnym bloku Rys. 3. Niektóre przykłady są podane w §2.
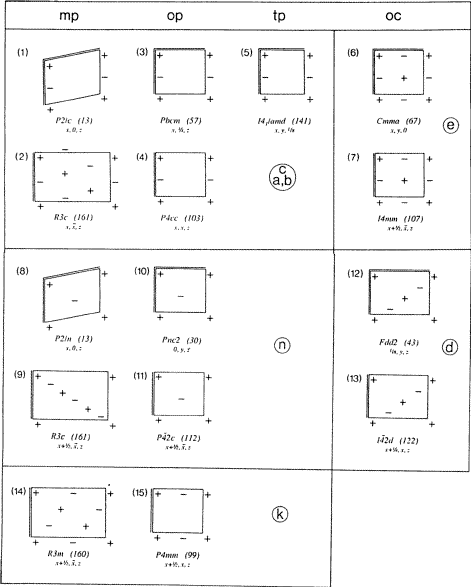
Na Rys. 3, Fischerowski spis wszystkich typów płaszczyzn ślizgowych jest przedstawiony w skróconej – choć nadal kompletnej – formie, w której więcej graficznego wyeksponowania nadano osiom krystalicznym. Dla każdego schematu podano jeden przykład jego występowania w grupie przestrzennej.
W niektórych grupach przestrzeni romboedrycznych ukośnie zorientowane płaszczyzny Ec, En i Ek występują z siatkami mp typu N, które można opisać przez potrójne centrowanie siatki ortogonalnej. Prostokątne potrójne oczko siatki N pokazane jest dla tych typów płaszczyzn ślizgowych na Rys. 3, diagramy (2), (9) i (14). Na diagramie (9) dostrzega się podobieństwo do innych diagramów n, takich jak (8) lub (10), jeśli w (9) rozważa się monokliniczną siatkę pierwotną siatki N z ukośnymi wektorami glejtu.
Symbole graficzne dla elementów symetrii
Istniejące symbole graficzne zdefiniowane i stosowane w ITA83 są uważane przez Komitet Ad-hoc za wystarczające z jednym wyjątkiem. Sytuacja jest zupełnie inna niż w przypadku symboli drukowanych, ponieważ na rysunkach kierunek rzutowania staje się dodatkowym parametrem. W terminach „rzut prostopadły” i „rzut równoległy” używanych poniżej, prostopadły i równoległy odnoszą się do orientacji kierunku rzutu w odniesieniu do płaszczyzny schodzenia.
Dla płaszczyzny Ee istnieje symbol 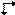 dla jej rzutu prostopadłego. Istniejące symbole graficzne dla rzutu równoległego płaszczyzny ślizgu Ee są jednak obarczone tą samą niejednoznacznością, co symbole drukowane. Wyrażają one wektor ślizgu albo równolegle, albo prostopadle do kierunku rzutowania, ale wybór jest arbitralny. Dlatego proponuje się nowy symbol dla rzutu równoległego płaszczyzny ślizgowej Ee, a mianowicie
dla jej rzutu prostopadłego. Istniejące symbole graficzne dla rzutu równoległego płaszczyzny ślizgu Ee są jednak obarczone tą samą niejednoznacznością, co symbole drukowane. Wyrażają one wektor ślizgu albo równolegle, albo prostopadle do kierunku rzutowania, ale wybór jest arbitralny. Dlatego proponuje się nowy symbol dla rzutu równoległego płaszczyzny ślizgowej Ee, a mianowicie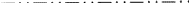
Przykłady płaszczyzn Ee.
Wszystkie płaszczyzny glejowe równoległe do dwóch osi w grupach przestrzennych Fmm2, Fmmm, ![]() ,
, ![]() i
i ![]() (nr 42, 69, 202, 225 i 226), jak również niektóre płaszczyzny w pięciu grupach przestrzennych wymienionych w §3.
(nr 42, 69, 202, 225 i 226), jak również niektóre płaszczyzny w pięciu grupach przestrzennych wymienionych w §3.
Diagonalnie zorientowane płaszczyzny Ee występują w grupach przestrzennych I4mm, I4cm, ![]() , I4/mmm, I4/mcm,
, I4/mmm, I4/mcm, ![]() i
i ![]() (nr. 107, 108, 121, 139, 140, 217 i 229).
(nr. 107, 108, 121, 139, 140, 217 i 229).
W ITA83 wszystkie te płaszczyzny Ee są narysowane raczej arbitralnie jako linie kropkowane lub przerywane w ich rzutach równoległych. Rys. 4 przedstawia schemat grupy przestrzennej I4cm (nr 108), zarówno w postaci pokazanej w ITA83, jak i z użyciem nowego symbolu.
Mimo że Ek jest nowym symbolem drukarskim, na diagramach ITA83 wszystkie płaszczyzny ślizgowe Ek zostały narysowane w sposób zadowalający, z zastosowaniem tych samych konwencji, jakie stosuje się dla płaszczyzn ślizgowych Ea/b/c. Podobnie jak w tych przypadkach, istnieje jeden specjalny wektor ślizgowy (prostopadły do osi kryształu w sieci N, por. Tabela 3). Gdy wektor ten jest np. równoległy do płaszczyzny projekcji, płaszczyzna Ek jest zawsze rysowana jako linia przerywana zgodnie z odpowiednią konwencją. Dlatego nie proponuje się żadnego nowego symbolu graficznego dla płaszczyzn ślizgowych Ek.
Przykłady płaszczyzn Ek.
Płaszczyzny takie łatwo znaleźć na diagramach ITA83 jako płaszczyzny równoległe tylko do jednej osi i rzutowane jako linie przerywane, np. xxz w P4bm i ![]() (nr 100 i 113). W szczególności, tabela 3 jest dokładnie zgodna z rozróżnieniem pokazanym pomiędzy płaszczyznami Ek i En. Patrz, na przykład, linie przerywane i kropkowane dla R3m i R3c (nr 160 i 161).
(nr 100 i 113). W szczególności, tabela 3 jest dokładnie zgodna z rozróżnieniem pokazanym pomiędzy płaszczyznami Ek i En. Patrz, na przykład, linie przerywane i kropkowane dla R3m i R3c (nr 160 i 161).
Symbole grup przestrzennych Hermanna-Mauguina
Znaki pojawiające się po literze kratowej w symbolu Hermanna-Mauguina (HM) grupy przestrzennej były pierwotnie przeznaczone do reprezentowania operacji generowania grupy. Na przykład, b było odbiciem b-glidu w płaszczyźnie zorientowanej zgodnie z jego pozycją w symbolu HM.
W praktyce, popularne, choć źle zdefiniowane elementy symetrii przejęły te operacje. W ten sposób b zaczęło być postrzegane jako płaszczyzna ślizgowa, Eb w naszej obecnej terminologii. Nie ma w tej reinterpretacji nic złego, z wyjątkiem sytuacji, gdy operacja należy do płaszczyzny ślizgowej Ee. Jeśli tak jest, na przykład, dla powyższego odbicia b-glide, to istnieje Ee, ale nie ma Eb-glide plane w odpowiedniej orientacji. W tym przypadku b staje się bardzo mylącym znakiem. Poza tym, stronniczość (nadana b w stosunku do a lub c) jest tak samo niepokojąca jak w przypadku symboli elementów symetrii traktowanych w §1.
W związku z tym, proponuje się zastąpienie takich mylących liter a lub b przez e we wszystkich pięciu symbolach HM, w których występują:
| Grupa przestrzenna nr. | 39 | 41 | 64 | 67 | 68 |
| Symbol w ITA83: | Abm2 | Aba2 | Cmca | Cmma | Ccca |
| Nowy symbol: | Aem2 | Aea2 | Cmce | Cmme | Ccce. |
Kolejną zaletą proponowanych nowych symboli jest to, że e – w przeciwieństwie do a lub b – jest neutralne i dlatego nie ulega zmianie przy permutacji osi.
Symbole drukowane dla operacji symetrii
Kompletny zestaw symboli drukowanych został zaprojektowany przez W. Fischera & E. Kocha (ITA83, §11.2) i był szeroko stosowany w sekcjach Symmetry Operations opisów grup przestrzennych.
W skrócie, każdy symbol składa się z maksymalnie trzech części. Pierwsza część to pojedynczy znak (czasem z indeksem), który opisuje rodzaj operacji. Kolejna(e) część(i) podaje(ją) składowe każdego odpowiedniego wektora przesunięcia lub translacji – zawsze w nawiasie – oraz współrzędne elementu geometrycznego operacji, w tej kolejności.
Komisja doraźna, po rozważeniu tego systemu, pragnie wprowadzić dwie modyfikacje dla odbić ślizgowych:
(i) zamiast obecnego pierwszego znaku (którym może być a, b, c, n, d lub g), należy zawsze pisać literę g;
(ii) należy zawsze pisać składowe wektora ślizgu (w nawiasach) w całości, w szczególności dla prostych odbić ślizgowych w płaszczyznach a-, b- lub c-, gdzie poprzednio były one pomijane.
Reguła (i) pomija informację o rodzaju płaszczyzny ślizgowej, do której należy dana operacja. Bardzo często informacja ta jest nieistotna lub nawet myląca. Dla płaszczyzn a/b/c tłumienie może zniszczyć istotną informację, ale strata jest przywrócona przez regułę (ii), jak pokazano w poniższym przykładzie.
Przez przyjęcie tych zmian, jednolitość symboli – również w odniesieniu do symboli dla obrotów – jest znacznie poprawiona. Na przykład, symbol odbicia ślizgowego na płaszczyźnie ![]() , z nietypowym wektorem ślizgowym
, z nietypowym wektorem ślizgowym ![]() , czyli
, czyli 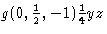 , jest teraz zgodny z symbolem prostego odbicia b-ślizgowego. W ITA83 było ono oznaczane przez
, jest teraz zgodny z symbolem prostego odbicia b-ślizgowego. W ITA83 było ono oznaczane przez ![]() , ale zasada (ii) zmienia je w
, ale zasada (ii) zmienia je w ![]() .
.
Powyższe reguły stosują się również do odbić ślizgowych należących do zbioru elementów płaszczyzny lustrzanej. Tak więc, jeśli składowa przesunięcia takiej operacji jest (0, 1, 2), to jej symbol zaczyna się od g(0, 1, 2), a nie od m(0, 1,2).
International Tables for Crystallography (1983). Vol. A, pod redakcją TH. HAHN, w szczególności §§ 1.1, 1.3, 1.4, 7 i 11. Dordrecht: Kluwer Academic Publishers.
International Tables for Crystallography (1989). Vol. A, 2nd, revised, ed., edited by TH. HAHN. Dordrecht: Kluwer Academic Publishers.
WOLFF, P. M. DE, BELOV, N. V., BERTAUT, E. F., BUERGER, M. J., DONNAY, J. D. H., FISCHER, W., HAHN, TH., KOPTSIK, V. A., MACKAY, A. L., WONDRATSCHEK, H., WILSON, A. J. C. & ABRAHAMS, S. C. (1985). Acta Cryst. A41, 278-280.
WOLFF, P. M. DE, BILLIET, Y., DONNAY, J. D. H., FISCHER, W., GALIULIN, R. B., GLAZER, A. M., SENECHAL, M., SHOEMAKER, D. P., WONDRATSCHEK, H., HAHN, TH., WILSON, A. J. C. & ABRAHAMS, S. C. (1989). Acta Cryst. A45, 494-499.
…wektory. Symbole płaszczyzny ślizgowej c, n i k dla trzech diagramów (2), (9) i (14) z Rys. 3 zostały oczywiście przypisane zgodnie z Tabelą 3. Jeden z członków Komitetu Ad-hoc (prof. Wondratschek) uważa, że symbol n dla diagramu (9) jest sprzeczny z tradycyjnymi pojęciami o n płaszczyznach. Proponuje on przypisanie specjalnego symbolu do diagramu (9). Propozycja ta nie uzyskała jednak odpowiedniego poparcia w Komitecie Ad-hoc.