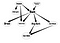
Dzisiaj postaram się wyjaśnić główne aspekty Belief Networks, szczególnie dla zastosowań, które mogą być związane z Social Network Analysis(SNA). Dodatkowo pokażę przykładową implementację tego typu sieci.

Do czego wykorzystujemy Sieci Bayesowskie?

Sieci Bayesowskie znajdują zastosowanie w wielu dziedzinach. Na przykład diagnostyka chorób, optymalizacja wyszukiwania w sieci, filtrowanie spamu, sieci regulacyjne genów itp. I ta lista może być rozszerzona. Głównym celem tych sieci jest próba zrozumienia struktury związków przyczynowo-skutkowych. Aby to wyjaśnić, rozważmy problem diagnozy choroby. Mając dane objawy i wynikającą z nich chorobę, konstruujemy naszą Sieć Przekonań i kiedy przychodzi nowy pacjent, możemy wnioskować, jaką chorobę lub choroby może mieć nowy pacjent poprzez podanie prawdopodobieństw dla każdej choroby. Podobnie, te relacje przyczynowości mogą być skonstruowane dla innych problemów i techniki wnioskowania mogą być zastosowane do interesujących wyników.

Quick Probability Review

Przed kontynuacją, aby odświeżyć naszą pamięć pozwól mi dać ci definicję warunkowej właściwości. Prawdopodobieństwo warunkowe to prawdopodobieństwo zmiennej losowej, gdy dana jest jakaś inna zmienna losowa. Pokazuje to

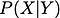
Jeżeli te dwie zmienne losowe są zależne,

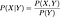
Jeżeli są niezależne, wtedy

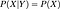
Matematyczna definicja sieci przekonań

Prawdopodobieństwa są obliczane w sieciach przekonań według następującego wzoru

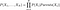
Jak można zrozumieć ze wzoru, aby móc obliczyć wspólny rozkład, musimy mieć prawdopodobieństwa warunkowe wskazywane przez sieć. Ale dalej, jeśli mamy wspólny rozkład, to możemy zacząć zadawać ciekawe pytania. Na przykład, w pierwszym przykładzie, pytamy o prawdopodobieństwo „RAIN” jeśli „SEASON” jest „WINTER” i „DOG BARK” jest „TRUE”.

Przykład sieci wierzących w Pythonie

Więc, myślę, że to wystarczy dla teorii i zobaczmy jakiś prawdziwy przykład z moim obecnym ulubionym językiem programowania Python ❤️ Przed kontynuacją, możesz znaleźć notatnik Jupyter, który napisałem tutaj.

# create the nodes
season = BbnNode(Variable(0, 'season', ), )
atmos_pres = BbnNode(Variable(1, 'atmos_press', ), )
allergies = BbnNode(Variable(2, 'allergies', ), )
rain = BbnNode(Variable(3, 'rain', ), )
grass = BbnNode(Variable(4, 'grass', ), )
umbrellas = BbnNode(Variable(5, 'umbrellas', ), )
dog_bark = BbnNode(Variable(6, 'dog_bark', ), )
cat_mood = BbnNode(Variable(7, 'cat_mood', ), )
cat_hide = BbnNode(Variable(8, 'cat_hide', ), )bbn = Bbn() \
.add_node(season) \
.add_node(atmos_pres) \
.add_node(allergies) \
.add_node(rain) \
.add_node(grass) \
.add_node(umbrellas) \
.add_node(dog_bark) \
.add_node(cat_mood) \
.add_node(cat_hide) \
.add_edge(Edge(season, allergies, EdgeType.DIRECTED)) \
.add_edge(Edge(season, umbrellas, EdgeType.DIRECTED)) \
.add_edge(Edge(season, rain, EdgeType.DIRECTED)) \
.add_edge(Edge(atmos_pres, rain, EdgeType.DIRECTED)) \
.add_edge(Edge(rain, grass, EdgeType.DIRECTED)) \
.add_edge(Edge(rain, umbrellas, EdgeType.DIRECTED)) \
.add_edge(Edge(rain, dog_bark, EdgeType.DIRECTED)) \
.add_edge(Edge(rain, cat_mood, EdgeType.DIRECTED)) \
.add_edge(Edge(dog_bark, cat_hide, EdgeType.DIRECTED)) \
.add_edge(Edge(cat_mood, cat_hide, EdgeType.DIRECTED))

Pierw opisaliśmy nasze węzły z prawdopodobieństwami warunkowymi. Powinieneś zauważyć, że pominąłem niektóre możliwe wartości stanu dla uproszczenia. Na przykład, zmienna sezonowa przyjmuje inne wartości „wiosna” i „jesień”. Idea jest więc ta sama.

Sprawdźmy, czy nasza sieć jest skonstruowana poprawnie, czy nie.

with warnings.catch_warnings():
warnings.simplefilter('ignore')
graph = convert_for_drawing(bbn)
pos = nx.nx_agraph.graphviz_layout(graph, prog='neato')plt.figure(figsize=(20, 10))
plt.subplot(121) 
labels = dict()
nx.draw(graph, pos=pos, with_labels=True, labels=labels)
plt.title('BBN DAG')

Ten fragment kodu dałby w rezultacie następujący wykres

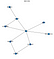
Widzisz więc, że ta sieć pasuje do mojego fantazyjnego rysunku na początku. Teraz, zróbmy trochę wnioskowania na tej sieci Belief Network.

# convert the BBN to a join tree
join_tree = InferenceController.apply(bbn)# insert an observation evidence
ev = EvidenceBuilder() \
.with_node(join_tree.get_bbn_node_by_name('season')) \
.with_evidence('winter', 1.0) \
.build()join_tree.set_observation(ev)# print the marginal probabilities
for node in join_tree.get_bbn_nodes():
potential = join_tree.get_bbn_potential(node)
print(node)
print(potential)
print('--------------------->')

Ten fragment kodu w zasadzie daje dowód sieci, która jest sezonem zimowym z prawdopodobieństwem 1.0. Zgodnie z tym dowodem, kiedy wykonujemy wnioskowanie, otrzymujemy następujące wyniki.

0|season|winter,summer
0=winter|1.00000
0=summer|0.00000
--------------------->
2|allergies|allergic,non_alergic
2=allergic|0.70000
2=non_alergic|0.30000
--------------------->
3|rain|rainy,sunny
3=rainy|0.80000
3=sunny|0.20000
--------------------->
4|grass|grass,no_grass
4=grass|0.70000
4=no_grass|0.30000
--------------------->
1|atmos_press|high,low
1=high|0.50000
1=low|0.50000
--------------------->
5|umbrellas|on,off
5=on|0.95200
5=off|0.04800
--------------------->
6|dog_bark|bark,not_bark
6=bark|0.66000
6=not_bark|0.34000
--------------------->
7|cat_mood|good,bad
7=good|0.23000
7=bad|0.77000
--------------------->
8|cat_hide|hide,show
8=hide|0.87150
8=show|0.12850
--------------------->

Kiedy dodamy kolejne dowody, takie jak pies nie szczeka

# convert the BBN to a join tree
join_tree = InferenceController.apply(bbn)# insert an observation evidence
ev = EvidenceBuilder() \
.with_node(join_tree.get_bbn_node_by_name('season')) \
.with_evidence('winter', 1.0) \
.build()ev2 = EvidenceBuilder() \
.with_node(join_tree.get_bbn_node_by_name('dog_bark')) \
.with_evidence('not_bark', 1.0) \
.build()join_tree.set_observation(ev)
join_tree.set_observation(ev2)# print the marginal probabilities
for node in join_tree.get_bbn_nodes():
potential = join_tree.get_bbn_potential(node)
print(node)
print(potential)
print('--------------------->')

otrzymujemy następujące wyniki wnioskowania

0|season|winter,summer
0=winter|1.00000
0=summer|0.00000
--------------------->
2|allergies|allergic,non_alergic
2=allergic|0.70000
2=non_alergic|0.30000
--------------------->
3|rain|rainy,sunny
3=rainy|0.47059
3=sunny|0.52941
--------------------->
4|grass|grass,no_grass
4=grass|0.53529
4=no_grass|0.46471
--------------------->
1|atmos_press|high,low
1=high|0.39706
1=low|0.60294
--------------------->
5|umbrellas|on,off
5=on|0.88941
5=off|0.11059
--------------------->
6|dog_bark|bark,not_bark
6=bark|0.00000
6=not_bark|1.00000
--------------------->
7|cat_mood|good,bad
7=good|0.52647
7=bad|0.47353
--------------------->
8|cat_hide|hide,show
8=hide|0.83162
8=show|0.16838
--------------------->

Czy widzisz różnicę? 😆 Wiele wartości prawdopodobieństwa zmieniło się, kiedy dodaliśmy dowody związane ze szczekaniem. Jest to zdecydowanie głupi przykład, ale miły do uzyskania intuicji.

Jak używać sieci bayesowskich w SNA ?

Sieci bayesowskie są bardzo potężnymi narzędziami do zrozumienia struktury związków przyczynowo-skutkowych pomiędzy zmiennymi. Po zaprojektowaniu modelu, nawet z małym zbiorem danych, może on powiedzieć różne rzeczy. Pytanie w tej części jest jak można uzyskać korzyści z sieci bayesowskich w SNA. Odpowiedź nie jest wyjątkowa, ale zacznijmy od głębokiej idei. W SNA, próbujemy zrozumieć strukturę sieci społecznej. Ponadto, staramy się zrozumieć znaczenie węzłów. Ale nie wiemy, jakie są wyniki naszych metryk ważności. To jest punkt, w którym sieci Bayesian Networks mają miejsce. Na przykład, jeśli uważasz, że znaczenie węzła jest spowodowane przez Centrality Degree i Centrality Link, możesz mieć następującą sieć.

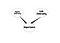
To jest bardzo naiwna Bayesian Network. Oprócz określenia ważności węzłów, dalszym zastosowaniem może być poszukiwanie pewnego specyficznego typu węzłów. Rozważmy sieć społeczną, w której jest kilka osób, które są potencjalnymi liderami i chcę ich wyszukać. Rozważmy następujący graf

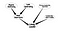
Ta nieco bardziej skomplikowana sieć pomoże nam określić niepewność węzłów związanych z byciem liderem.

Innym zastosowaniem będzie wnioskowanie o powiązaniach. Nowe linki mogą być wywnioskowane z istniejących. Na przykład, z członkostwa w grupie w sieci społecznej, prawdopodobne członkostwo link może być wywnioskowane. Chodziło mi o to, że możemy modelować nowe powiązanie między użytkownikami i grupami, biorąc pod uwagę istniejące powiązania. Zobacz następujący diagram modelu

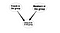
Więc, są to podstawowe przykłady jak Sieci Bayesowskie mogą być zastosowane w SNA. Ten temat nie jest zbyt dobrze zbadany, ale myślę, że może być bardzo przydatny do dalszego badania.

Wniosek

Trudną rzeczą w sieciach Bayesian jest projektowanie. Szczególnie, gdy myślisz o SNA, konstruowanie mapowania z Social Network z Bayesian Network jest sztuką niż nauką 😃 Ale raz zrobiłeś sztukę pracy i zaprojektował swój model bardzo dobrze, te poręczne narzędzia mogą powiedzieć ci wiele rzeczy. Jak wiemy, że Bayesian Networks są stosowane w ogromnych rodzajów obszarów. To działało bardzo dobrze w większości przypadków. Dlatego mocno wierzę, że możemy zrobić bardzo głębokie wnioski na Social Networks, jak również.

Dla dalszych badań z SNA i Bayesian Networks, proszę być na bieżąco 🚀

.