Stromové datové struktury mají mnoho využití a je dobré mít základní znalosti o jejich fungování. Stromy jsou základem dalších velmi používaných datových struktur, jako jsou Mapy a Množiny. Také se používají v databázích k rychlému vyhledávání. HTML DOM používá stromovou datovou strukturu k reprezentaci hierarchie prvků. V tomto příspěvku se budeme zabývat různými typy stromů, jako jsou binární stromy, binární vyhledávací stromy, a jejich implementací.
V předchozím příspěvku jsme prozkoumali datové struktury Graph, které jsou zobecněným případem stromů. Pojďme se začít učit, co jsou to stromové datové struktury!
Tento příspěvek je součástí výukového seriálu:
Učení o datových strukturách a algoritmech (DSA) pro začátečníky
-
Úvod do časové složitosti algoritmu a notace Big O
-
Osm časových složitostí, které by měl znát každý programátor
-
Datové struktury pro začátečníky: Stromy Datové struktury pro začátečníky
-
Datové struktury pro začátečníky
-
Stromy Datové struktury pro začátečníky 👈 jste zde
-
Samostatné binární vyhledávací stromy
-
Příloha I: Stromy: základní pojmy
Strom je datová struktura, kde uzel může mít nula nebo více potomků. Každý uzel obsahuje určitou hodnotu. Stejně jako u grafů se spojení mezi uzly nazývá hrany. Strom je typ grafu, ale ne všechny grafy jsou stromy (o tom později).
Těmto datovým strukturám se říká „stromy“, protože datová struktura připomíná strom 🌳. Začíná kořenovým uzlem a větví se jeho potomky a nakonec jsou zde listy.
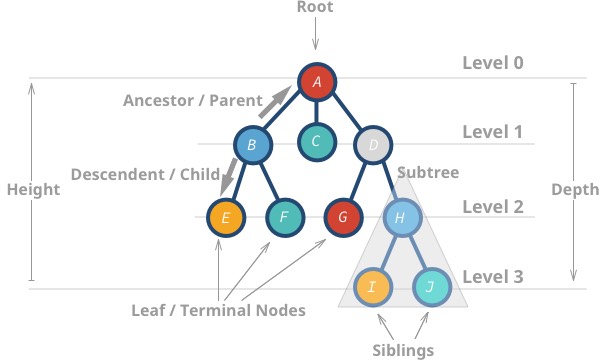
Zde jsou uvedeny některé vlastnosti stromů:
- Nejvyšší uzel se nazývá kořen.
- Uzel bez potomků se nazývá listový nebo koncový uzel.
- Výška (h) stromu je vzdálenost (počet hran) mezi nejvzdálenějším listem a kořenem.
-
Amá výšku 3 -
Imá výšku 0
-
- Hloubka neboli úroveň uzlu je vzdálenost mezi kořenem a daným uzlem.
-
Hmá hloubku 2 -
Bmá hloubku 1
-
Implementace jednoduché stromové datové struktury
Jak jsme viděli dříve, uzel stromu je pouze datová struktura s hodnotou a odkazy na své potomky.
Uveďme si příklad stromového uzlu:
1
2
3
4
5
6class TreeNode {
constructor(value) {
this.value = value;
this.descendants = ;
}
}Strom se třemi potomky můžeme vytvořit následujícím způsobem:
1
2
3
4
5
6
7
8
9
10// create nodes with values
const abe = new TreeNode('Abe');
const homer = new TreeNode('Homer');
const bart = new TreeNode('Bart');
const lisa = new TreeNode('Lisa');
const maggie = new TreeNode('Maggie');
// associate root with is descendants
abe.descendants.push(homer);
homer.descendants.push(bart, lisa, maggie);To je vše; máme stromovou datovou strukturu!
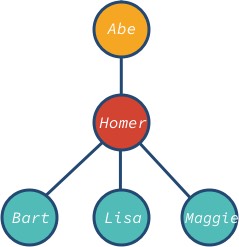
Uzel
abeje kořen abart,lisaamaggiejsou listové uzly stromu. Všimněte si, že uzel stromu může mít různé potomky:Stromové datové struktury mají mnoho aplikací, například:
- Mapy
- Soubory
- Databáze
- Prioritní fronty
- Dotazování do LDAP (Lightweight Directory Access Protocol)
- Představení objektového modelu dokumentu (DOM) pro HTML na webových stránkách.
Binární stromy
Stromové uzly mohou mít nula nebo více potomků. Pokud však má strom nejvýše dvě děti, pak se nazývá binární strom.
Úplné, úplné a dokonalé binární stromy
Podle toho, jak jsou uzly v binárním stromu uspořádány, může být úplný, úplný a dokonalý:
- Úplný binární strom: každý uzel má přesně 0 nebo 2 děti (ale nikdy 1).
- Úplný binární strom: když jsou všechny úrovně kromě poslední plné uzlů.
- Dokonalý binární strom: když jsou všechny úrovně (včetně poslední) plné uzlů.
Podívejte se na tyto příklady:
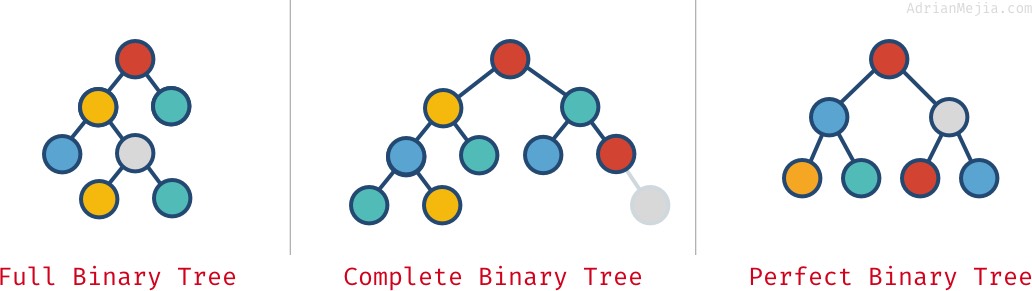
Tyto vlastnosti se vždy navzájem nevylučují. Můžete jich mít více:
- Dokonalý strom je vždy úplný a plný.
- Dokonalé binární stromy mají přesně `2^k – 1` uzlů, kde
kje poslední úroveň stromu (počínaje 1).
- Dokonalé binární stromy mají přesně `2^k – 1` uzlů, kde
- Plný strom není vždy
full.- Tak jako v našem „úplném“ příkladu, protože má rodiče s jediným potomkem. Pokud bychom odstranili nejpravější šedý uzel, pak bychom měli úplný a plný strom, ale ne dokonalý.
- Úplný strom není vždy úplný a dokonalý.
Binární vyhledávací strom (BST)
Binární vyhledávací stromy nebo zkráceně BST jsou zvláštní aplikací binárních stromů. BST má nejvýše dva uzly (jako všechny binární stromy). Hodnoty jsou však takové, že hodnota levého potomka musí být menší než hodnota rodiče a hodnota pravého potomka musí být vyšší.
Duplikáty: Některé BST duplicity nepovolují, zatímco jiné přidávají stejné hodnoty jako pravý potomek. Jiné implementace mohou počítat s případem duplicity (té se budeme věnovat později).
Implementujme binární vyhledávací strom!“
Implementace BST
BST jsou velmi podobné naší předchozí implementaci stromu. Jsou zde však některé rozdíly:
- Uzly mohou mít nanejvýš dva potomky: levého a pravého.
- Hodnoty uzlů musí být uspořádány jako
left < parent < right.
Tady je uzel stromu. Velmi podobný tomu, co jsme dělali předtím, ale přidali jsme několik šikovných getterů a setterů pro levé a pravé děti. Všimněte si, že se také uchovává odkaz na rodiče a aktualizujeme ho při každém přidání dětí.
TreeNode.jsCode 1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32const LEFT = 0;
const RIGHT = 1;
class TreeNode {
constructor(value) {
this.value = value;
this.descendants = ;
this.parent = null;
}
get left() {
return this.descendants;
}
set left(node) {
this.descendants = node;
if (node) {
node.parent = this;
}
}
get right() {
return this.descendants;
}
set right(node) {
this.descendants = node;
if (node) {
node.parent = this;
}
}
}Ok, zatím můžeme přidat levé a pravé dítě. Nyní provedeme třídu BST, která vynucuje pravidlo
left < parent < right.BinarySearchTree.js linkUrl linkText 1
2
3
4
5
6
7
8
9
10
11
12
13
class BinarySearchTree {
constructor() {
this.root = null;
this.size = 0;
}
add(value) { /* ... */ }
find(value) { /* ... */ }
remove(value) { /* ... */ }
getMax() { /* ... */ }
getMin() { /* ... */ }
}Provedeme vložení.
Vkládání uzlů BST
Pro vložení uzlu do binárního stromu postupujeme takto:
- Pokud je strom prázdný, první uzel se stane kořenem a je hotovo.
- Porovnejte hodnotu kořene/rodiče, pokud je vyšší, jděte doprava, pokud je nižší, jděte doleva. Pokud je stejná, pak hodnota již existuje, takže můžete zvýšit počet duplicit (multiplicitu).
- Pak opakujte postup č. 2, dokud nenajdeme prázdné místo pro vložení nového uzlu.
Udělejme si názorný příklad, jak vložit 30, 40, 10, 15, 12, 50:
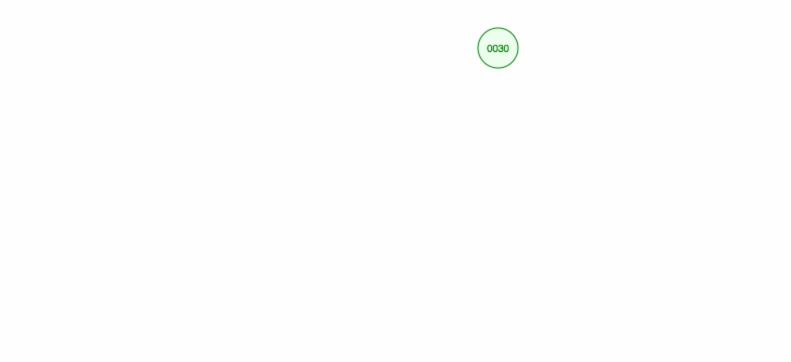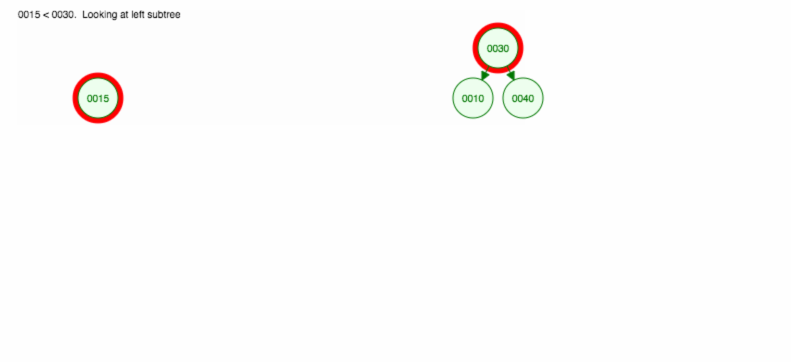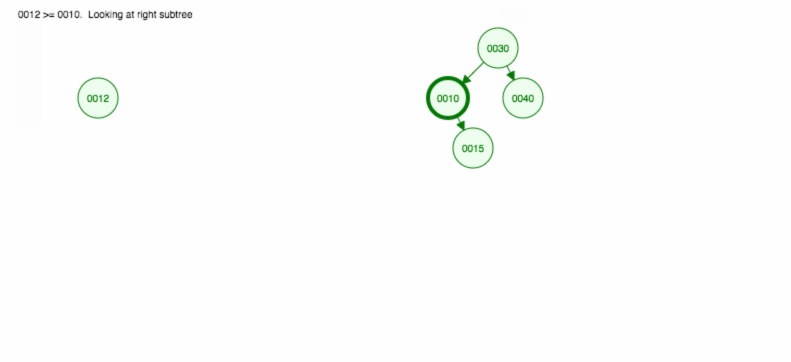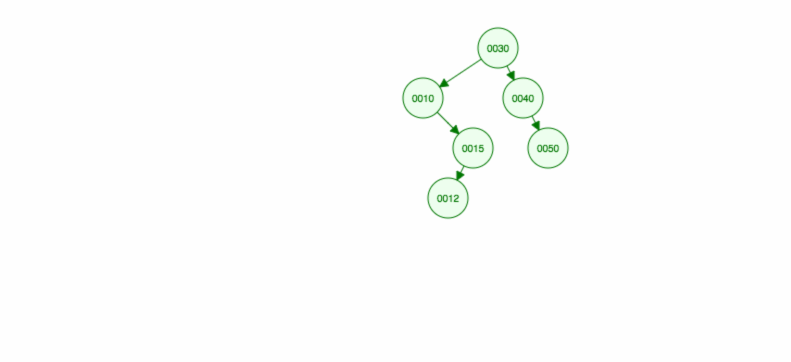
Vkládání můžeme implementovat takto:
BinarySearchTree.prototype.addFull Code 1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19add(value) {
const newNode = new TreeNode(value);
if (this.root) {
const { found, parent } = this.findNodeAndParent(value);
if (found) { // duplicated: value already exist on the tree
found.meta.multiplicity = (found.meta.multiplicity || 1) + 1;
} else if (value < parent.value) {
parent.left = newNode;
} else {
parent.right = newNode;
}
} else {
this.root = newNode;
}
this.size += 1;
return newNode;
}Používáme pomocnou funkci
findNodeAndParent. Pokud jsme zjistili, že uzel již ve stromu existuje, zvýšíme čítačmultiplicity. Podívejme se, jak je tato funkce implementována:BinarySearchTree.prototype.findNodeAndParentFull Kód 1
2
3
4
5
6
7
8
9
10
11
12
13
14findNodeAndParent(value) {
let node = this.root;
let parent;
while (node) {
if (node.value === value) {
break;
}
parent = node;
node = ( value >= node.value) ? node.right : node.left;
}
return { found: node, parent };
}findNodeAndParentprochází strom a hledá hodnotu. Začíná u kořene (řádek 2) a pak jde doleva nebo doprava podle hodnoty (řádek 10). Pokud hodnota již existuje, vrátí uzelfounda také jeho rodiče. V případě, že uzel neexistuje, vrátíme ještěparent.BST Odstranění uzlu
Víme, jak vložit a vyhledat hodnotu. Nyní budeme implementovat operaci smazání. Je to trochu složitější než přidávání, proto si ji vysvětlíme na následujících případech:
Smazání listového uzlu (0 dětí)
1
2
3
4
5
6
730 30
/ \ remove(12) / \
10 40 ---------> 10 40
\ / \ \ / \
15 35 50 15 35 50
/
12*Odebereme odkaz na rodiče uzlu (15), aby byl nulový.
Smazání uzlu s jedním dítětem.
1
2
3
4
530 30
/ \ remove(10) / \
10* 40 ---------> 15 40
\ / \ / \
15 35 50 35 50V tomto případě přejdeme k rodiči (30) a nahradíme potomka (10) potomkem dítěte (15).
Odstranění uzlu se dvěma dětmi
1
2
3
4
530 30
/ \ remove(40) / \
15 40* ---------> 15 50
/ \ /
35 50 35Odstraníme uzel 40, který má dvě děti (35 a 50). Dítě rodiče (30) (40) nahradíme jeho pravým dítětem (50). Levé dítě (35) pak ponecháme na stejném místě jako předtím, takže z něj musíme udělat levé dítě uzlu 50.
Jiný způsob odstranění uzlu 40 je přesunout levé dítě (35) nahoru a pravé dítě (50) pak ponechat tam, kde bylo.
1
2
3
4
530
/ \
15 35
\
50Obojí způsob je v pořádku, pokud zachováte vlastnost binárního vyhledávacího stromu:
left < parent < right.Odstranění kořene.
1
2
3
4
530* 50
/ \ remove(30) /
15 50 ---------> 35
/ /
35 15Odstranění kořene je velmi podobné dříve diskutovanému odstranění uzlů s 0, 1 nebo 2 potomky. Jediný rozdíl je v tom, že poté musíme aktualizovat odkaz na kořen stromu.
Tady je animace toho, co jsme probrali.
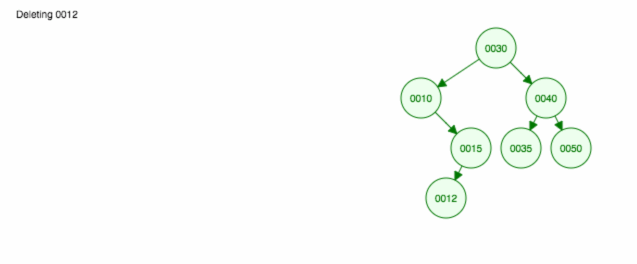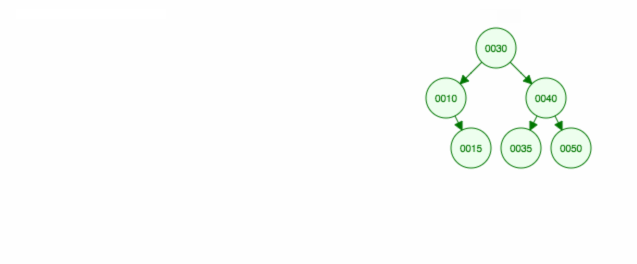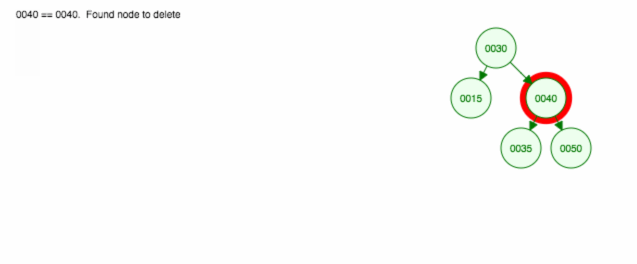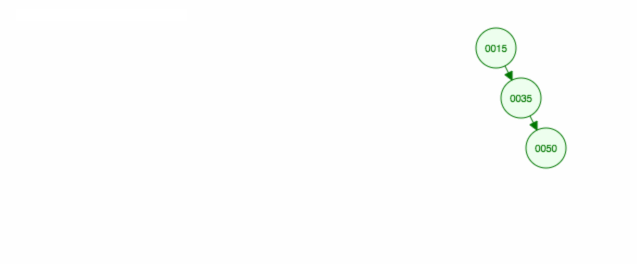
Animace posouvá levé dítě/strom nahoru a pravé dítě/strom ponechává na místě.
Teď, když máme dobrou představu, jak by to mělo fungovat, to implementujme:
BinarySearchTree.prototype.removeFull Code 1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23remove(value) {
const nodeToRemove = this.find(value);
if (!nodeToRemove) return false;
// Combine left and right children into one subtree without nodeToRemove
const nodeToRemoveChildren = this.combineLeftIntoRightSubtree(nodeToRemove);
if (nodeToRemove.meta.multiplicity && nodeToRemove.meta.multiplicity > 1) {
nodeToRemove.meta.multiplicity -= 1; // handle duplicated
} else if (nodeToRemove === this.root) {
// Replace (root) node to delete with the combined subtree.
this.root = nodeToRemoveChildren;
this.root.parent = null; // clearing up old parent
} else {
const side = nodeToRemove.isParentLeftChild ? 'left' : 'right';
const { parent } = nodeToRemove; // get parent
// Replace node to delete with the combined subtree.
parent = nodeToRemoveChildren;
}
this.size -= 1;
return true;
}Tady jsou některé hlavní body implementace:
- Nejprve vyhledáme, zda uzel existuje. Pokud neexistuje, vrátíme false a je hotovo!
- Pokud uzel, který chceme odstranit, existuje, spojíme levé a pravé děti do jednoho podstromu.
- Nahradíme uzel, který chceme odstranit, kombinovaným podstromem.
Funkce, která spojí levý do pravého podstromu, je následující:
BinarySearchTree.prototype.combineLeftIntoRightSubtreeFull Code 1
2
3
4
5
6
7
8combineLeftIntoRightSubtree(node) {
if (node.right) {
const leftmost = this.getLeftmost(node.right);
leftmost.left = node.left;
return node.right;
}
return node.left;
}Řekněme, že chceme zkombinovat následující strom a chystáme se odstranit uzel
30. Chceme smíchat levý podstrom 30 s pravým. Výsledek je následující:1
2
3
4
5
6
730* 40
/ \ / \
10 40 combine(30) 35 50
\ / \ -----------> /
15 35 50 10
\
15Pokud z nového podstromu uděláme kořenový, pak uzel
30již nebude!Průchod binárním stromem
Existují různé způsoby průchodu binárním stromem v závislosti na pořadí, v jakém jsou uzly navštíveny: v pořadí in-order, pre-order a post-order. Také je můžeme použítDFSaBFS, které jsme se naučili z příspěvkugraph. projděme si každý z nich.
In-order traversal
In-order traversal navštěvuje uzly v tomto pořadí: vlevo, nadřazený, vpravo.
BinarySearchTree.prototype.inOrderTraversalÚplný kód 1
2
3
4
5* inOrderTraversal(node = this.root) {
if (node.left) { yield* this.inOrderTraversal(node.left); }
yield node;
if (node.right) { yield* this.inOrderTraversal(node.right); }
}Použijeme tento strom k vytvoření příkladu:
1
2
3
4
5
6
710
/ \
5 30
/ / \
4 15 40
/
3Při procházení by se vypsaly následující hodnoty:
3, 4, 5, 10, 15, 30, 40. Pokud je strom BST, pak budou uzly seřazeny vzestupně jako v našem příkladu.Post-order traversal
Post-order traversal navštěvuje uzly v tomto pořadí: vlevo, vpravo, rodič.
BinarySearchTree.prototype.postOrderTraversalFull Code 1
2
3
4
5* postOrderTraversal(node = this.root) {
if (node.left) { yield* this.postOrderTraversal(node.left); }
if (node.right) { yield* this.postOrderTraversal(node.right); }
yield node;
}Post-order traversal by vypsal následující hodnoty:
3, 4, 5, 15, 40, 30, 10.Předobjednávkové procházení a DFS
Předobjednávkové procházení navštěvuje uzly v tomto pořadí: nadřazený, levý, pravý.
BinarySearchTree.prototype.preOrderTraversalPlný kód 1
2
3
4
5* preOrderTraversal(node = this.root) {
yield node;
if (node.left) { yield* this.preOrderTraversal(node.left); }
if (node.right) { yield* this.preOrderTraversal(node.right); }
}Předřazené procházení by vypsalo následující hodnoty:
10, 5, 4, 3, 30, 15, 40. Toto pořadí čísel je stejný výsledek, jaký bychom dostali, kdybychom spustili prohledávání do hloubky (DFS).BinarySearchTree.prototype.dfsFull Code 1
2
3
4
5
6
7
8
9
10
11
12* dfs() {
const stack = new Stack();
stack.add(this.root);
while (!stack.isEmpty()) {
const node = stack.remove();
yield node;
// reverse array, so left gets removed before right
node.descendants.reverse().forEach(child => stack.add(child));
}
}Pokud si potřebujete osvěžit DFS, podrobně jsme se mu věnovali v příspěvku Graf.
Breadth-First Search (BFS)
Podobně jako DFS můžeme BFS implementovat tak, že
StackprohodímeQueue:BinarySearchTree.prototype.bfsFull Code 1
2
3
4
5
6
7
8
9
10
11* bfs() {
const queue = new Queue();
queue.add(this.root);
while (!queue.isEmpty()) {
const node = queue.remove();
yield node;
node.descendants.forEach(child => queue.add(child));
}
}Pořadí BFS je:
10, 5, 30, 4, 15, 40, 3Vyvážené vs. nevyvážené stromy
Dosud jsme se zabývali tím, jak
add,removeafindprvky. Nehovořili jsme však o době běhu. Zamysleme se nad nejhoršími scénáři.Řekněme, že chceme sčítat čísla vzestupně.
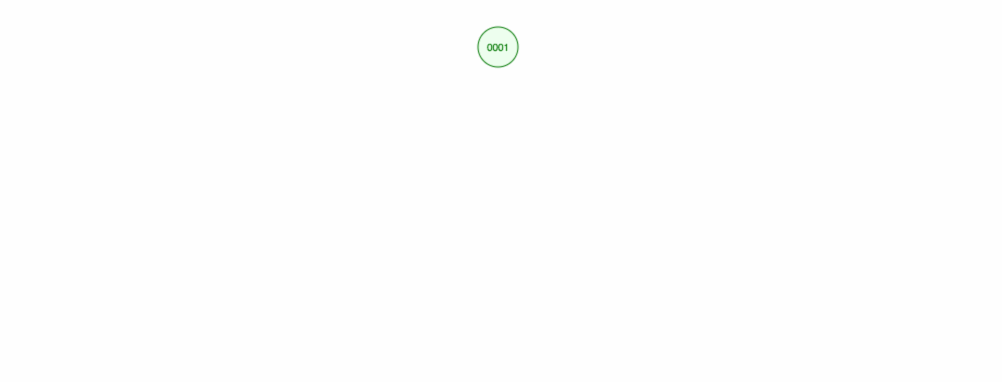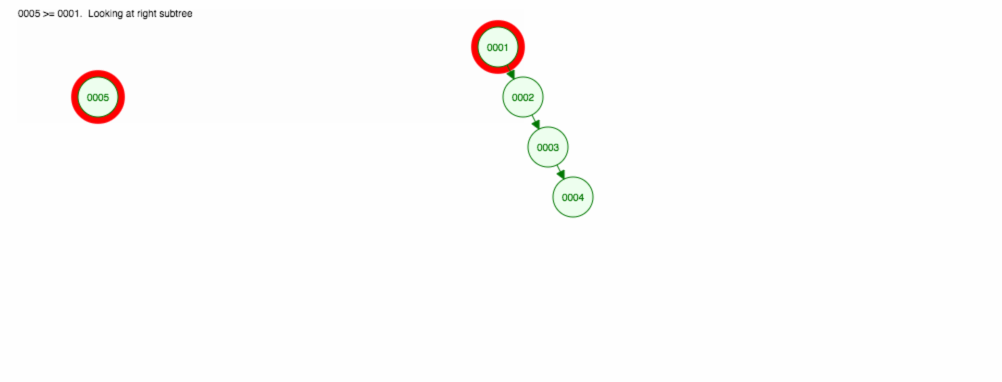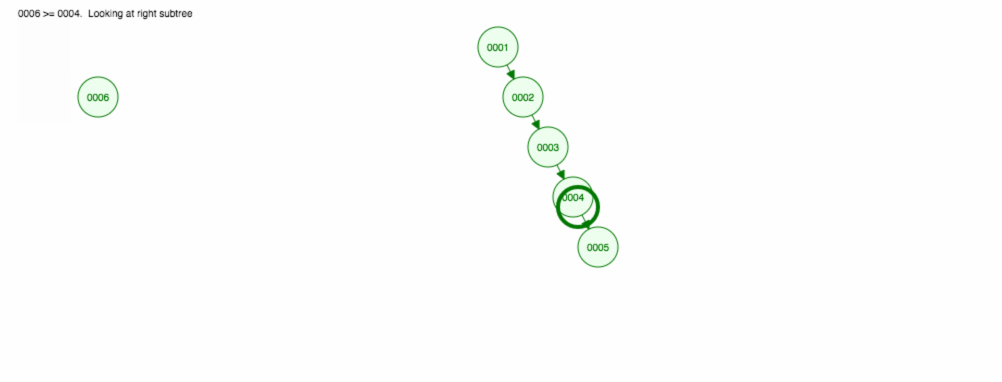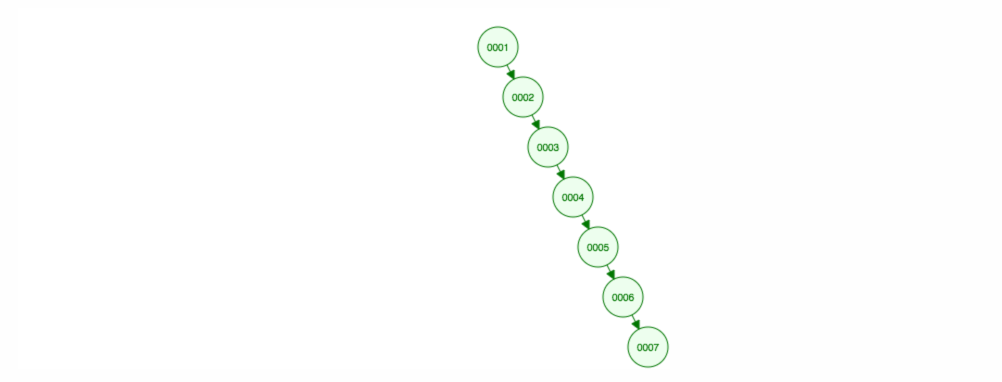
Skončíme tak, že všechny uzly budou na pravé straně! Takový nevyvážený strom není o nic lepší než LinkedList, takže nalezení prvku by trvalo O(n). 😱
Hledat něco v nevyváženém stromu je jako hledat slovo ve slovníku stránku po stránce. Když je strom vyvážený, můžete slovník otevřít uprostřed a odtud víte, jestli máte jít doleva nebo doprava v závislosti na abecedě a hledaném slově.
Musíme najít způsob, jak strom vyvážit!“
Pokud by byl strom vyvážený, mohli bychom prvky najít za O(log n), místo abychom procházeli každý uzel. Řekněme si, co znamená vyvážený strom.
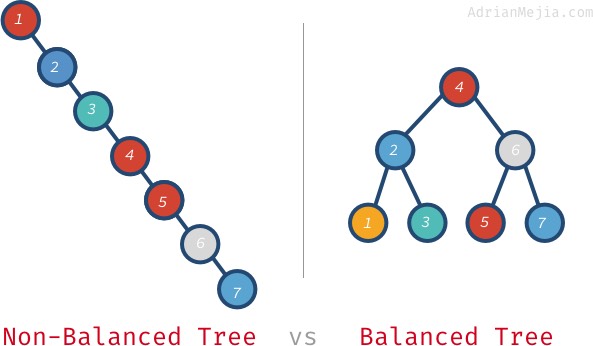
Pokud hledáme
7v nevyváženém stromu, musíme projít od 1 do 7. Ve vyváženém stromu však navštívíme:4,6a7. U větších stromů je to ještě horší. Pokud máme milion uzlů, hledání neexistujícího prvku může vyžadovat návštěvu celého milionu, zatímco ve vyváženém stromu. Přitom stačí 20 návštěv! To je obrovský rozdíl!“Tento problém vyřešíme v příštím příspěvku pomocí samovyvážených stromů (stromů AVL).
Shrnutí
U stromů jsme probrali mnoho témat. Shrňme to odrážkami:
- Strom je datová struktura, kde uzel má 0 nebo více potomků/dětí.
- Stromové uzly nemají cykly (jsou acyklické). Pokud cykly má, jedná se místo toho o datovou strukturu Graph.
- Stromy se dvěma nebo méně potomky se nazývají: Binární strom
- Když je binární strom seřazen tak, že levá hodnota je menší než rodič a pravá dětí je vyšší, pak a pouze tehdy máme binární vyhledávací strom.
- Strom můžete navštívit před/po/v pořadí.
- Nevyvážený má časovou složitost O(n). 🤦🏻
- Vyvážený má časovou složitost O(log n). 🎉