Struktury danych drzew mają wiele zastosowań i dobrze jest mieć podstawowe zrozumienie, jak one działają. Drzewa są podstawą dla innych bardzo używanych struktur danych, takich jak Mapy i Zestawy. Są one również używane w bazach danych do szybkiego wyszukiwania. HTML DOM używa drzewiastej struktury danych do reprezentowania hierarchii elementów. W tym poście poznamy różne typy drzew, takie jak drzewa binarne, drzewa wyszukiwania binarnego i jak je zaimplementować.

W poprzednim poście poznaliśmy struktury danych Graph, które są uogólnionym przypadkiem drzew. Zacznijmy się uczyć, czym są struktury danych drzewa!

Ten post jest częścią serii samouczków:

Learning Data Structures and Algorithms (DSA) for Beginners

1. Wprowadzenie do złożoności czasowej algorytmów i notacji Big O

2. Osiem złożoności czasowych, które każdy programista powinien znać

3. Struktury danych dla początkujących: Arrays, HashMaps, and Lists

4. Graph Data Structures for Beginners

5. Trees Data Structures for Beginners 👈 you are here

6. Self-balanced Binary Search Trees

7. Appendix I: Analysis of Recursive Algorithms

Drzewa: podstawowe pojęcia

Drzewo to struktura danych, w której węzeł może mieć zero lub więcej dzieci. Każdy węzeł zawiera wartość. Podobnie jak w grafach, połączenia między węzłami są nazywane krawędziami. Drzewo jest rodzajem grafu, ale nie wszystkie grafy są drzewami (więcej na ten temat później).

Te struktury danych są nazywane „drzewami”, ponieważ struktura danych przypomina drzewo 🌳. Zaczyna się od węzła korzeniowego i rozgałęzia się z jego potomkami, a na końcu są liście.

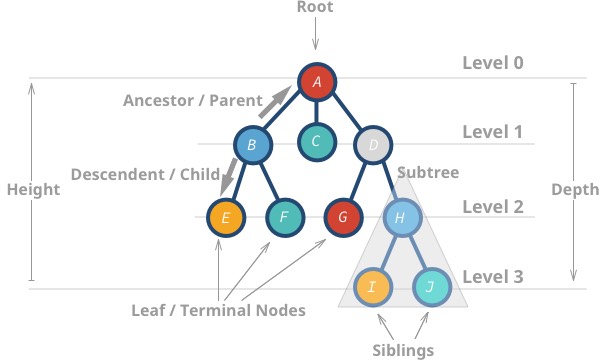
Oto niektóre właściwości drzew:

• Najwyższy węzeł jest nazywany korzeniem.
• Węzeł bez dzieci jest nazywany węzłem liści lub węzłem końcowym.
• Wysokość (h) drzewa to odległość (liczba krawędzi) między najdalszym liściem a korzeniem.
  • A ma wysokość 3
  • I ma wysokość 0
• Głębokość lub poziom węzła to odległość między korzeniem a danym węzłem.
  • H ma głębokość 2
  • B ma głębokość 1

Implementacja prostej drzewiastej struktury danych

Jak widzieliśmy wcześniej, węzeł drzewa to po prostu struktura danych z wartością i łączami do jej potomków.

Oto przykład węzła drzewa:

1
2
3
4
5
6

class TreeNode {
constructor(value) {
this.value = value;
this.descendants = ;
}
}

Możemy utworzyć drzewo z 3 potomkami w następujący sposób:

1
2
3
4
5
6
7
8
9
10

// create nodes with values
const abe = new TreeNode('Abe');
const homer = new TreeNode('Homer');
const bart = new TreeNode('Bart');
const lisa = new TreeNode('Lisa');
const maggie = new TreeNode('Maggie');
// associate root with is descendants
abe.descendants.push(homer);
homer.descendants.push(bart, lisa, maggie);

To wszystko; mamy drzewiastą strukturę danych!

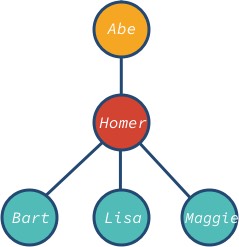
Węzeł abe jest korzeniem, a bart, lisa i maggie są węzłami liści drzewa. Zauważmy, że węzeł drzewa może mieć różnych potomków: 0, 1, 3, lub dowolną inną wartość.

Drzewiaste struktury danych mają wiele zastosowań, takich jak:

• Mapy
• Zbiory
• Bazy danych
• Kolejki priorytetowe
• Pytanie o LDAP (Lightweight Directory Access Protocol)
• Prezentowanie modelu DOM (Document Object Model) dla HTML na stronach internetowych.

Drzewa binarne

Węzły drzewa mogą mieć zero lub więcej dzieci. Jednakże, gdy drzewo ma co najwyżej dwoje dzieci, wtedy nazywa się drzewem binarnym.

Pełne, kompletne i doskonałe drzewa binarne

Zależnie od tego, jak węzły są ułożone w drzewie binarnym, może być ono pełne, kompletne i doskonałe:

• Pełne drzewo binarne: każdy węzeł ma dokładnie 0 lub 2 dzieci (ale nigdy 1).
• Kompletne drzewo binarne: gdy wszystkie poziomy oprócz ostatniego są pełne węzłów.
• Doskonałe drzewo binarne: gdy wszystkie poziomy (w tym ostatni) są pełne węzłów.

Spójrz na te przykłady:

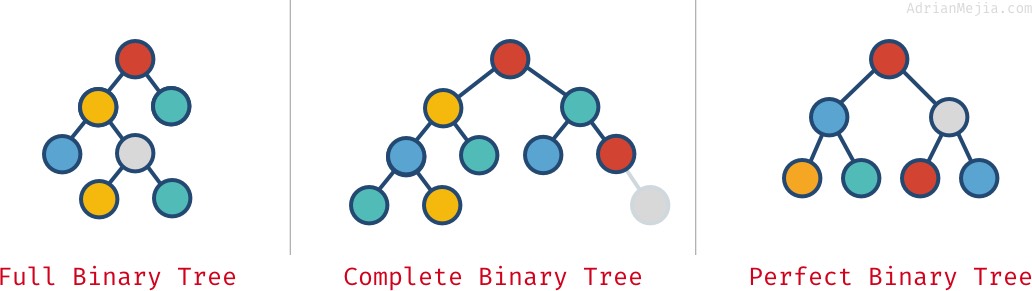
Właściwości te nie zawsze się wykluczają. Możesz mieć więcej niż jedną:

• Doskonałe drzewo jest zawsze kompletne i pełne.
  • Doskonałe drzewa binarne mają dokładnie `2^k – 1` węzłów, gdzie k jest ostatnim poziomem drzewa (zaczynając od 1).
• Kompletne drzewo nie zawsze jest full.
  • Tak jak w naszym „kompletnym” przykładzie, ponieważ ma rodzica z tylko jednym dzieckiem. Jeśli usuniemy najbardziej prawy szary węzeł, wtedy mielibyśmy kompletne i pełne drzewo, ale nie doskonałe.
• Pełne drzewo nie zawsze jest kompletne i doskonałe.

Binarne Drzewo Wyszukiwania (BST)

Binarne Drzewa Wyszukiwania lub w skrócie BST są szczególnym zastosowaniem drzew binarnych. BST ma co najwyżej dwa węzły (jak wszystkie drzewa binarne). Jednak wartości są takie, że lewa wartość dzieci musi być mniejsza niż rodzic, a prawe dzieci muszą być wyższe.

Duplikaty: Niektóre BST nie pozwalają na duplikaty, podczas gdy inne dodają te same wartości jako prawe dziecko. Inne implementacje mogą zliczać przypadki duplikatów (zajmiemy się tym później).

Zaimplementujmy Binarne Drzewo Wyszukiwania!

Implementacja BST

BST są bardzo podobne do naszej poprzedniej implementacji drzewa. Istnieją jednak pewne różnice:

• Węzły mogą mieć, co najwyżej, tylko dwa dzieci: lewe i prawe.
• Wartości węzłów muszą być uporządkowane jako left < parent < right.

Tutaj znajduje się węzeł drzewa. Bardzo podobny do tego, co zrobiliśmy wcześniej, ale dodaliśmy kilka poręcznych getterów i setterów dla lewego i prawego dziecka. Zauważ, że przechowuje również referencję do rodzica, a my aktualizujemy ją za każdym razem, gdy dodajemy dzieci.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32

const LEFT = 0;
const RIGHT = 1;
class TreeNode {
constructor(value) {
this.value = value;
this.descendants = ;
this.parent = null;
}
get left() {
return this.descendants;
}
set left(node) {
this.descendants = node;
if (node) {
node.parent = this;
}
}
get right() {
return this.descendants;
}
set right(node) {
this.descendants = node;
if (node) {
node.parent = this;
}
}
}

Ok, jak dotąd, możemy dodać lewe i prawe dziecko. Teraz zróbmy klasę BST, która egzekwuje regułę left < parent < right.

1
2
3
4
5
6
7
8
9
10
11
12
13

class BinarySearchTree {
constructor() {
this.root = null;
this.size = 0;
}
add(value) { /* ... */ }
find(value) { /* ... */ }
remove(value) { /* ... */ }
getMax() { /* ... */ }
getMin() { /* ... */ }
}

Zaimplementujmy wstawianie.

Wstawianie węzłów BST

Aby wstawić węzeł do drzewa binarnego, wykonujemy następujące czynności:

1. Jeśli drzewo jest puste, pierwszy węzeł staje się korzeniem i gotowe.
2. Porównaj wartość korzenia/rodzica, jeśli jest wyższa idź w prawo, jeśli niższa idź w lewo. Jeśli jest taka sama, to wartość już istnieje, więc możesz zwiększyć liczbę duplikatów (multiplicity).
3. Powtarzaj #2 aż znajdziemy puste miejsce do wstawienia nowego węzła.

Zróbmy ilustrację, jak wstawić 30, 40, 10, 15, 12, 50:

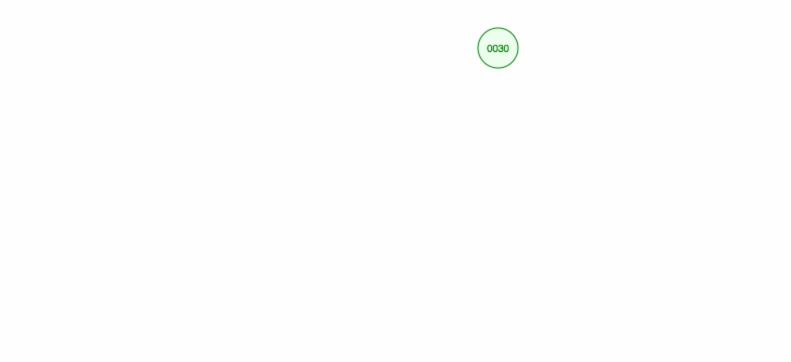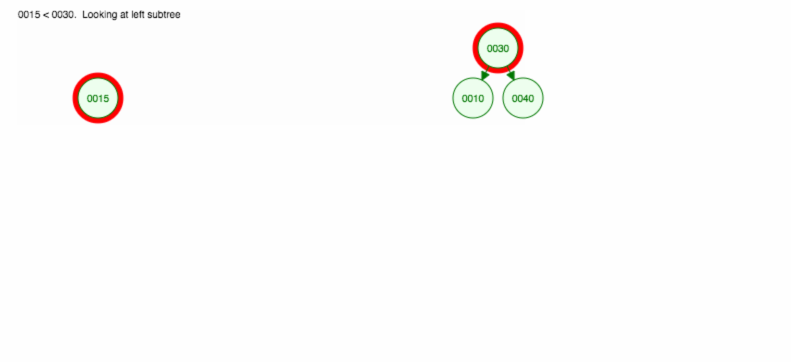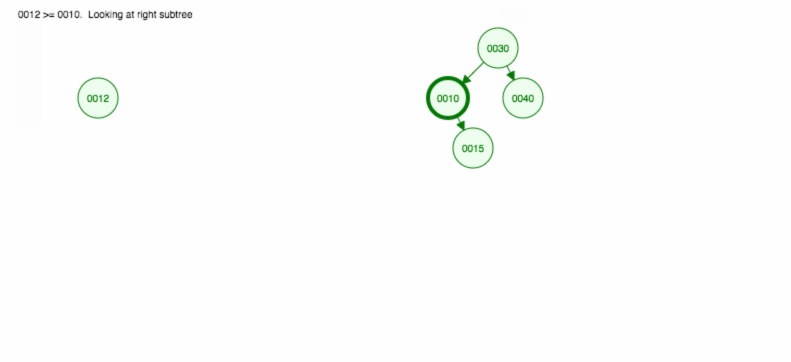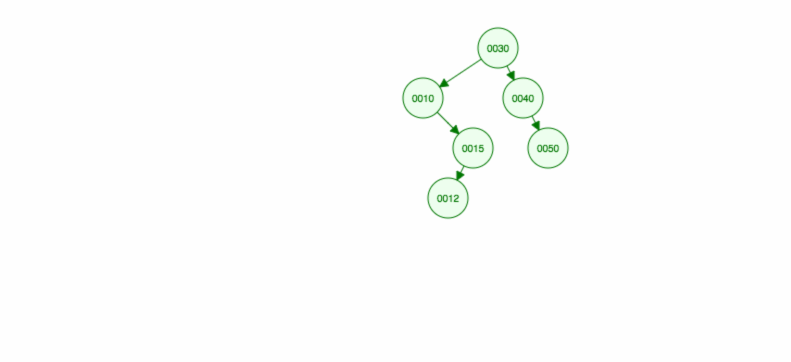
Możemy zaimplementować insert w następujący sposób:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19

add(value) {
const newNode = new TreeNode(value);
if (this.root) {
const { found, parent } = this.findNodeAndParent(value);
if (found) { // duplicated: value already exist on the tree
found.meta.multiplicity = (found.meta.multiplicity || 1) + 1;
} else if (value < parent.value) {
parent.left = newNode;
} else {
parent.right = newNode;
}
} else {
this.root = newNode;
}
this.size += 1;
return newNode;
}

Wykorzystujemy funkcję pomocniczą o nazwie findNodeAndParent. Jeśli stwierdziliśmy, że dany węzeł już istnieje w drzewie, to zwiększamy licznik multiplicity. Zobaczmy, jak ta funkcja jest zaimplementowana:

1
2
3
4
5
6
7
8
9
10
11
12
13
14

findNodeAndParent(value) {
let node = this.root;
let parent;
while (node) {
if (node.value === value) {
break;
}
parent = node;
node = ( value >= node.value) ? node.right : node.left;
}
return { found: node, parent };
}

findNodeAndParent przechodzi przez drzewo, szukając wartości. Zaczyna od korzenia (linia 2), a następnie idzie w lewo lub w prawo w zależności od wartości (linia 10). Jeśli wartość już istnieje, zwróci węzeł found oraz jego rodzica. W przypadku, gdy węzeł nie istnieje, nadal zwracamy parent.

BST Node Deletion

Wiemy już jak wstawiać i wyszukiwać wartości. Teraz zajmiemy się implementacją operacji usuwania. Jest to trochę bardziej skomplikowane niż dodawanie, więc wyjaśnijmy to na przykładzie następujących przypadków:

Usuwanie węzła liścia (0 dzieci)

1
2
3
4
5
6
7

 30 30
/ \ remove(12) / \
10 40 ---------> 10 40
\ / \ \ / \
15 35 50 15 35 50
/
12*

Usuwamy referencję z rodzica węzła (15), aby był null.

Usuwanie węzła z jednym dzieckiem.

1
2
3
4
5

 30 30
/ \ remove(10) / \
10* 40 ---------> 15 40
\ / \ / \
15 35 50 35 50

W tym przypadku przechodzimy do rodzica (30) i zastępujemy dziecko (10) dzieckiem (15).

Usuwanie węzła z dwojgiem dzieci

1
2
3
4
5

 30 30
/ \ remove(40) / \
15 40* ---------> 15 50
/ \ /
35 50 35

Usuwamy węzeł 40, który ma dwoje dzieci (35 i 50). Zamieniamy dziecko rodzica (30) (40) na prawe dziecko (50). Następnie zachowujemy lewe dziecko (35) w tym samym miejscu co poprzednio, więc musimy uczynić je lewym dzieckiem 50.

Innym sposobem na usunięcie węzła 40 jest przesunięcie lewego dziecka (35) w górę, a następnie zachowanie prawego dziecka (50) tam, gdzie było.

1
2
3
4
5

 30
/ \
15 35
\
50

Każdy z tych sposobów jest ok, o ile zachowujesz własność drzewa wyszukiwania binarnego: left < parent < right.

Usuwanie korzenia.

1
2
3
4
5

 30* 50
/ \ remove(30) /
15 50 ---------> 35
/ /
35 15

Usuwanie korzenia jest bardzo podobne do usuwania węzłów z 0, 1, lub 2 dziećmi omówionych wcześniej. Jedyna różnica polega na tym, że potem musimy zaktualizować referencję korzenia drzewa.

Tutaj animacja tego, o czym mówiliśmy.

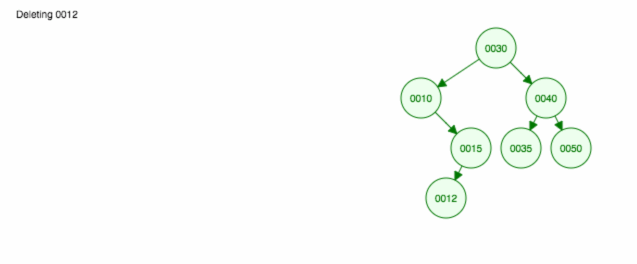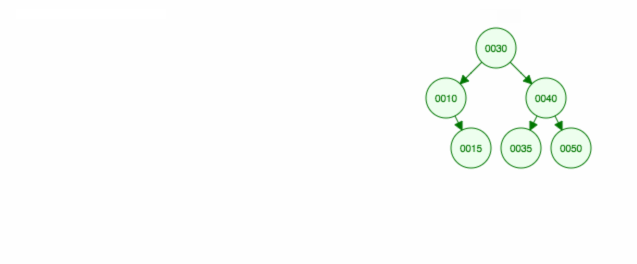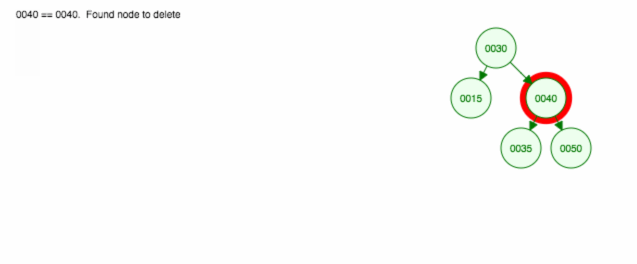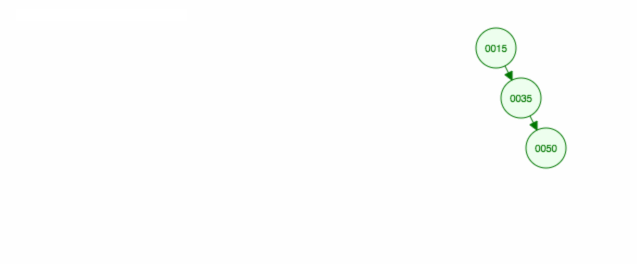
Animacja przesuwa lewe dziecko/poddrzewo w górę i utrzymuje prawe dziecko/poddrzewo na miejscu.

Teraz, gdy mamy już dobry pomysł, jak to powinno działać, zaimplementujmy to:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23

remove(value) {
const nodeToRemove = this.find(value);
if (!nodeToRemove) return false;
// Combine left and right children into one subtree without nodeToRemove
const nodeToRemoveChildren = this.combineLeftIntoRightSubtree(nodeToRemove);
if (nodeToRemove.meta.multiplicity && nodeToRemove.meta.multiplicity > 1) {
nodeToRemove.meta.multiplicity -= 1; // handle duplicated
} else if (nodeToRemove === this.root) {
// Replace (root) node to delete with the combined subtree.
this.root = nodeToRemoveChildren;
this.root.parent = null; // clearing up old parent
} else {
const side = nodeToRemove.isParentLeftChild ? 'left' : 'right';
const { parent } = nodeToRemove; // get parent
// Replace node to delete with the combined subtree.
parent = nodeToRemoveChildren;
}
this.size -= 1;
return true;
}

Oto kilka najważniejszych punktów implementacji:

• Po pierwsze, sprawdzamy czy węzeł istnieje. Jeśli nie, zwracamy false i gotowe!
• Jeśli węzeł do usunięcia istnieje, to łączymy lewe i prawe dzieci w jedno poddrzewo.
• Zastąp węzeł do usunięcia połączonym poddrzewem.

Funkcja, która łączy lewe w prawe poddrzewo jest następująca:

1
2
3
4
5
6
7
8

combineLeftIntoRightSubtree(node) {
if (node.right) {
const leftmost = this.getLeftmost(node.right);
leftmost.left = node.left;
return node.right;
}
return node.left;
}

Na przykład, powiedzmy, że chcemy połączyć następujące drzewo i mamy zamiar usunąć węzeł 30. Chcemy wymieszać lewe poddrzewo 30 z prawym. Wynik jest taki:

1
2
3
4
5
6
7

 30* 40
/ \ / \
10 40 combine(30) 35 50
\ / \ -----------> /
15 35 50 10
\
15

Jeśli uczynimy nowe poddrzewo korzeniem, to węzeł 30 już nie istnieje!

Przekształcanie drzewa binarnego

Istnieją różne sposoby przekręcania drzewa binarnego, w zależności od kolejności odwiedzania węzłów: in-order, pre-order i post-order. Możemy również użyćDFSiBFS,których nauczyliśmy się wgraph post.Przejdźmy przez każdy z nich.

In-Order Traversal

In-order traversal odwiedza węzły w tej kolejności: left, parent, right.

1
2
3
4
5

* inOrderTraversal(node = this.root) {
if (node.left) { yield* this.inOrderTraversal(node.left); }
yield node;
if (node.right) { yield* this.inOrderTraversal(node.right); }
}

Użyjmy tego drzewa do wykonania przykładu:

1
2
3
4
5
6
7

 10
/ \
5 30
/ / \
4 15 40
/
3

In-order traversal wypisałby następujące wartości: 3, 4, 5, 10, 15, 30, 40. Jeśli drzewo jest BST, to węzły będą posortowane w kolejności rosnącej, jak w naszym przykładzie.

Post-Order Traversal

Post-order traversal odwiedza węzły w tej kolejności: left, right, parent.

1
2
3
4
5

* postOrderTraversal(node = this.root) {
if (node.left) { yield* this.postOrderTraversal(node.left); }
if (node.right) { yield* this.postOrderTraversal(node.right); }
yield node;
}

Post-order traversal wypisałby następujące wartości: 3, 4, 5, 15, 40, 30, 10.

Pre-Order Traversal and DFS

Pre-order traversal visit nodes on this order: parent, left, right.

1
2
3
4
5

* preOrderTraversal(node = this.root) {
yield node;
if (node.left) { yield* this.preOrderTraversal(node.left); }
if (node.right) { yield* this.preOrderTraversal(node.right); }
}

Pre-order traversal wypisałby następujące wartości: 10, 5, 4, 3, 30, 15, 40. Ta kolejność liczb jest tym samym wynikiem, który otrzymalibyśmy, gdybyśmy uruchomili Depth-First Search (DFS).

1
2
3
4
5
6
7
8
9
10
11
12

* dfs() {
const stack = new Stack();
stack.add(this.root);
while (!stack.isEmpty()) {
const node = stack.remove();
yield node;
// reverse array, so left gets removed before right
node.descendants.reverse().forEach(child => stack.add(child));
}
}

Jeśli potrzebujesz odświeżenia na temat DFS, omówiliśmy to szczegółowo w poście Graph.

Breadth-First Search (BFS)

Podobnie do DFS, możemy zaimplementować BFS poprzez zamianę Stack na Queue:

1
2
3
4
5
6
7
8
9
10
11

* bfs() {
const queue = new Queue();
queue.add(this.root);
while (!queue.isEmpty()) {
const node = queue.remove();
yield node;
node.descendants.forEach(child => queue.add(child));
}
}

Porządek BFS to: 10, 5, 30, 4, 15, 40, 3

Balanced vs. Non-balanced Trees

Do tej pory omówiliśmy sposób add, remove, oraz find elementów. Nie rozmawialiśmy jednak o czasie działania. Zastanówmy się nad najgorszymi scenariuszami.

Powiedzmy, że chcemy dodawać liczby w kolejności rosnącej.

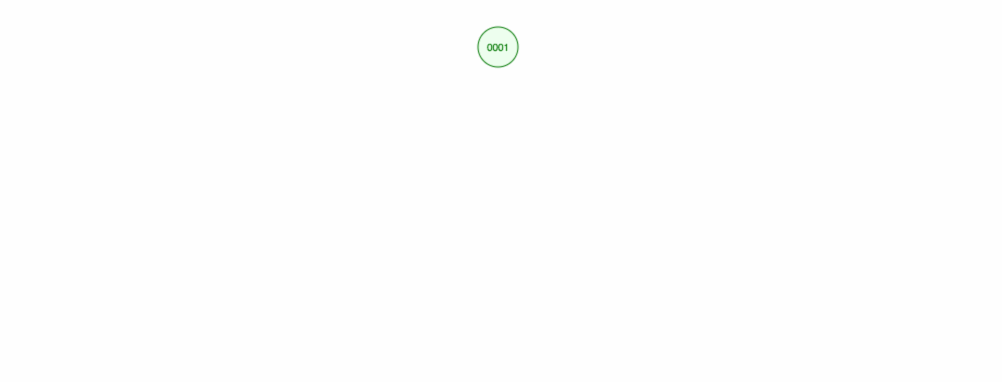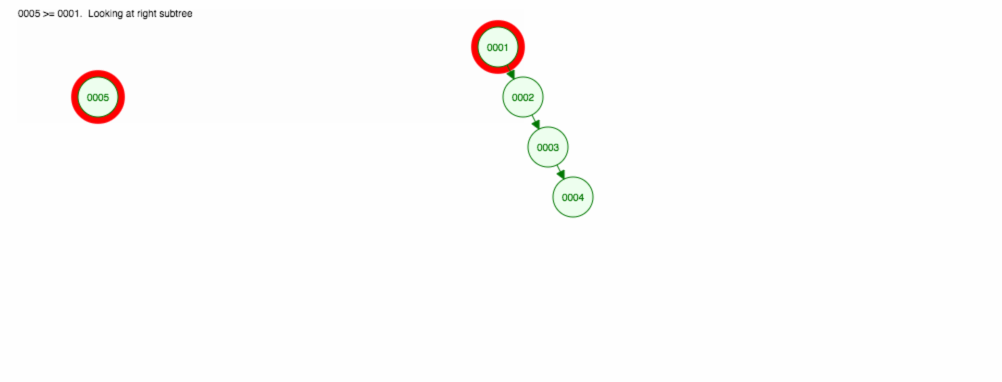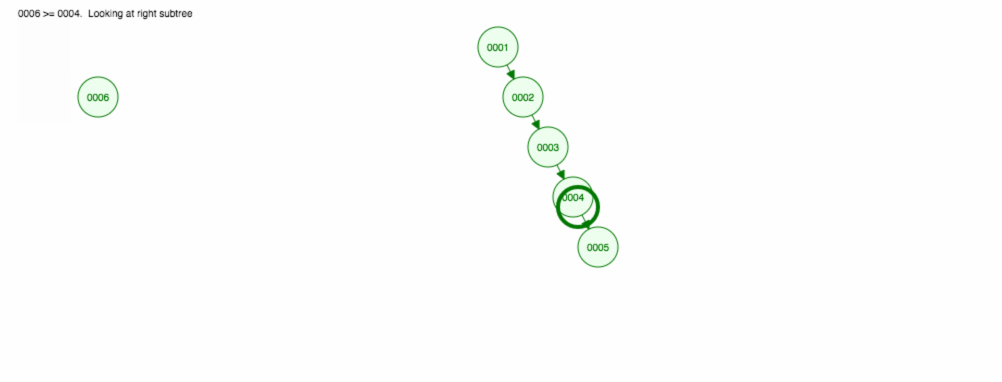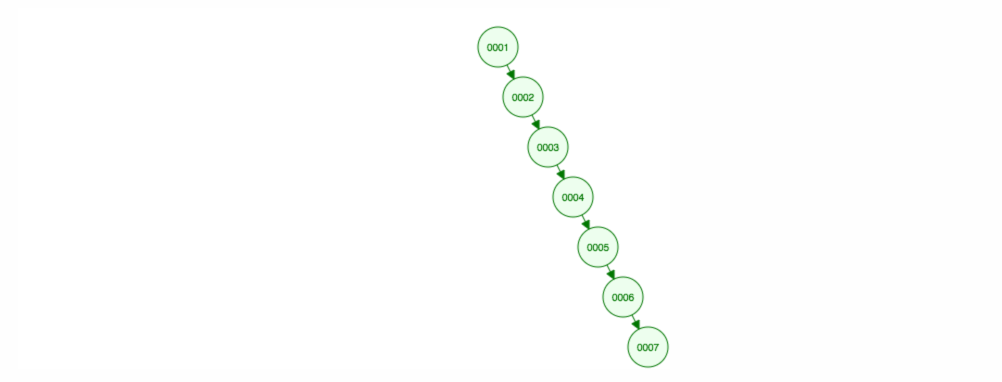
Skończymy z wszystkimi węzłami po prawej stronie! To niezrównoważone drzewo nie jest lepsze niż LinkedList, więc znalezienie elementu zajęłoby O(n). 😱

Szukanie czegoś w niezbalansowanym drzewie jest jak szukanie słowa w słowniku strona po stronie. Kiedy drzewo jest zrównoważone, możesz otworzyć słownik w środku i stamtąd wiesz, czy musisz iść w lewo czy w prawo, w zależności od alfabetu i słowa, którego szukasz.

Musimy znaleźć sposób na zrównoważenie drzewa!

Gdyby drzewo było zrównoważone, moglibyśmy znaleźć elementy w O(log n) zamiast przechodzić przez każdy węzeł. Porozmawiajmy o tym, co oznacza zbalansowane drzewo.

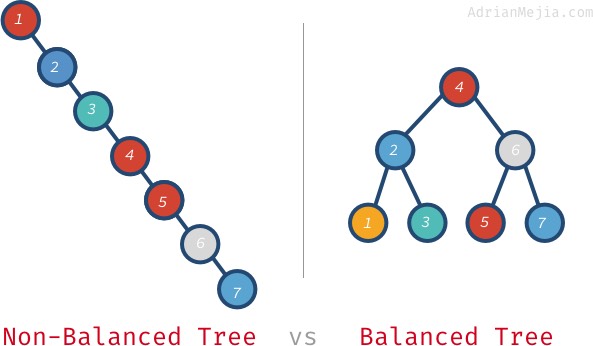
Jeśli szukamy 7 w niezbalansowanym drzewie, musimy przejść od 1 do 7. Jednak w zbalansowanym drzewie odwiedzamy: 4, 6, oraz 7. Z większymi drzewami jest jeszcze gorzej. Jeśli masz milion węzłów, szukanie nieistniejącego elementu może wymagać odwiedzenia wszystkich milionów, podczas gdy na zrównoważonym drzewie. To potrzebuje tylko 20 wizyt! To ogromna różnica!

Rozwiążemy ten problem w następnym poście, używając drzew samozrównoważonych (drzewa AVL).

Podsumowanie

Objęliśmy wiele zagadnień związanych z drzewami. Podsumujmy to kulami:

• Drzewo jest strukturą danych, w której węzeł ma 0 lub więcej potomków/dzieci.
• Węzły drzewa nie mają cykli (acyklicznych). Jeśli ma cykle, to jest to struktura danych Graph zamiast.
• Drzewa z dwoma dziećmi lub mniej są nazywane: Binary Tree
• Gdy drzewo binarne jest posortowane tak, że lewa wartość jest mniejsza niż rodzic, a prawe dzieci są wyższe, wtedy i tylko wtedy mamy Binary Search Tree.
• Możesz odwiedzić drzewo w sposób pre/post/in-order fashion.
• Niezrównoważony ma złożoność czasową O(n). 🤦🏻
• Zrównoważony ma złożoność czasową O(log n). 🎉