初心者のための JavaScript におけるツリーデータ構造｜Adrian Mejia Blog

Tree データ構造は多くの用途を持っており、それらがどのように機能するかを基本的に理解しておくことは良いことだと思います。木は、マップや集合のような他の非常に使用されるデータ構造の基礎となります。また、データベースで迅速な検索を実行するために使用されます。 HTML DOMは、要素の階層構造を表現するためにツリーデータ構造を使用しています。この投稿では、2 進木、2 進検索木などさまざまな種類の木について調べ、それらをどのように実装するかを説明します。

前回の投稿では、木の一般化したケースであるグラフデータ構造について調べました。では、さっそく木データ構造がどのようなものかを学んでいきましょう

Learning Data Structures and Algorithms (DSA) for Beginners

アルゴリズムの時間複雑性と Big O notation 入門
Eight time complexities that every programmer should know
Data Structures for Beginners.Of.Pirates

Data Structures for Beginners: 配列、ハッシュマップ、リスト
初心者のためのグラフデータ構造
初心者のための木データ構造 👈 ここにいます
自己平衡二分探索木
Appendix I: 再帰的アルゴリズムの分析

木：基本概念

木は、ノードが0以上の子を持つことができるデータ構造である。各ノードには値が含まれます。グラフのように、ノード間の接続はエッジと呼ばれます。木はグラフの一種ですが、すべてのグラフが木であるわけではありません (詳細は後述します)。

これらのデータ構造は、データ構造が木🌳に似ていることから「木」と呼ばれています。ルートノードから始まり、その子孫で分岐し、最後に葉があります。

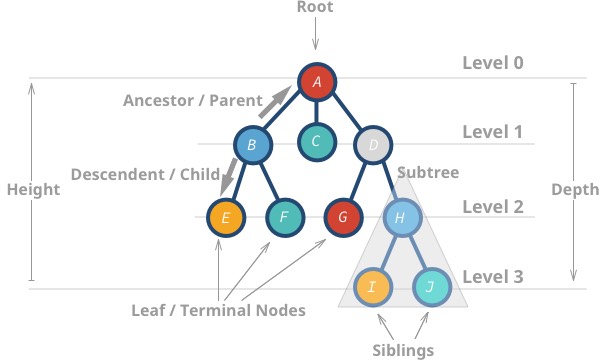
以下に、木のプロパティをいくつか示します。

木の高さ（h）は、一番遠い葉から根までの距離（エッジ数）です。

Aは高さが3
Iは0

ノードの深さは、根と当該ノードの間の距離です。

H の深さは 2
B の深さは 1

簡単な木データ構造の実装

前に見たように、木ノードは値とその子孫へのリンクを持つ単なるデータ構造です。

以下はツリーノードの例です：

class TreeNode {
constructor(value) {
this.value = value;
this.descendants = ;
}
}

以下のように3つの子孫を持つツリーを作成することができます。

// create nodes with values
const abe = new TreeNode('Abe');
const homer = new TreeNode('Homer');
const bart = new TreeNode('Bart');
const lisa = new TreeNode('Lisa');
const maggie = new TreeNode('Maggie');
// associate root with is descendants
abe.descendants.push(homer);
homer.descendants.push(bart, lisa, maggie);

以上で木のデータ構造ができました!

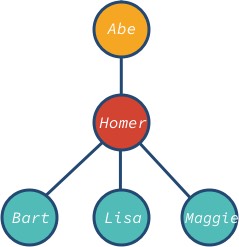
ノード abe がルートで、bart, lisa, maggie が木の葉のノードになります。ツリーのノードは異なる子孫を持つことができることに注意。

ツリーデータ構造は、次のような多くのアプリケーションを持っています：

マップ
セット
データベース
優先キュー
LDAP（軽量ディレクトリアクセスプロトコル）
ウェブサイト上の HTML 用ドキュメントオブジェクトモデル (DOM) を表現すること。

Binary Trees

Trees ノードはゼロまたはそれ以上の子を持つことができます。しかし、木が最大 2 つの子を持つ場合、それはバイナリツリーと呼ばれます。

完全、完全、および完全なバイナリツリー

バイナリツリーのノードの配置方法によって、完全、完全、完全が可能です。

完全二分木：最後のレベルを除くすべてのレベルがノードで満杯のとき。

完全二分木：すべてのレベル（最後のレベルを含む）がノードで満杯のとき。

完全な木は常に完全でいっぱいです。
- 完全な二分木は正確に`2^k – 1`個のノードを持ち、kは木の最後のレベル（1 から始まる）。
完全な木は常にfullではない、我々の「完全」例のように、たった1個の子を持つ親を持っているのだから。右端の灰色のノードを削除すると、完全な木になるが、完全ではない。

完全な木が常に完全で完璧とは限らない。

二項探索木 (BST)

二項探索木（BST）は、二項木の特定のアプリケーションである。 BSTは（他の2分木と同様に）最大で2つのノードを持つ。ただし、左の子の値は親より小さく、右の子の値は親より大きくなければならない

。 BSTによっては、重複を許可しないものもあれば、右の子として同じ値を追加するものもあります。

バイナリサーチツリーを実装しよう！

BST Implementation

BST は以前のツリーの実装に非常によく似ています。しかし、いくつかの違いがあります。

ノードは最大で左と右の2つの子しか持てません。

ノードの値は left < parent < right のように並べる必要があります。前にやったことと非常によく似ていますが、左と右の子供のためにいくつかの便利なゲッターとセッターを追加しました。

TreeNode.jsCode

const LEFT = 0;
const RIGHT = 1;
class TreeNode {
constructor(value) {
this.value = value;
this.descendants = ;
this.parent = null;
}
get left() {
return this.descendants;
}
set left(node) {
this.descendants = node;
if (node) {
node.parent = this;
}
}
get right() {
return this.descendants;
}
set right(node) {
this.descendants = node;
if (node) {
node.parent = this;
}
}
}

OK、ここまでは、左と右の子供を追加することができました。では、left < parent < rightルールを強制するBSTクラスをやってみましょう。

BinarySearchTree.js linkUrl linkText


class BinarySearchTree {
constructor() {
this.root = null;
this.size = 0;
}
add(value) { /* ... */ }
find(value) { /* ... */ }
remove(value) { /* ... */ }
getMax() { /* ... */ }
getMin() { /* ... */ }
}

insertionを実施しましょう。

BST ノード挿入

2分木にノードを挿入するには、次のようにします。

木が空の場合、最初のノードがルートとなり、終了します。
ルートと親の値を比較して、高ければ右に、低ければ左に移動します。
新しいノードを挿入するための空のスロットが見つかるまで、#2 を繰り返し行います。

30, 40, 10, 15, 12, 50 を挿入する方法を説明します。

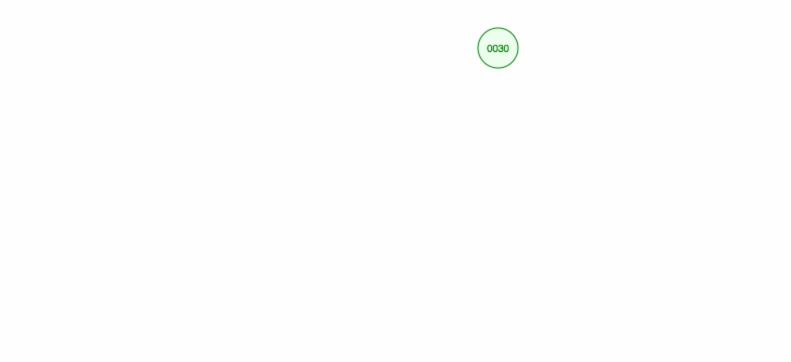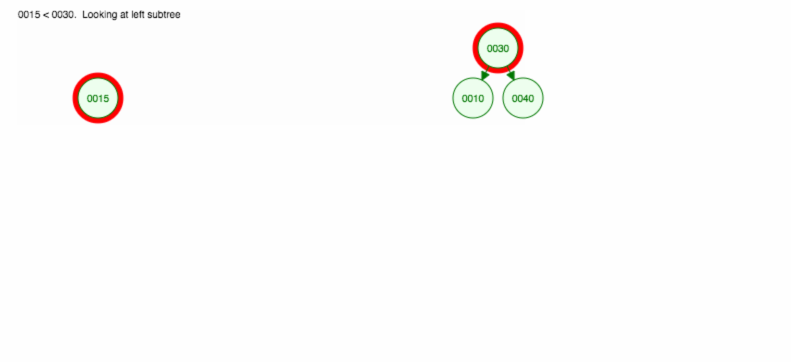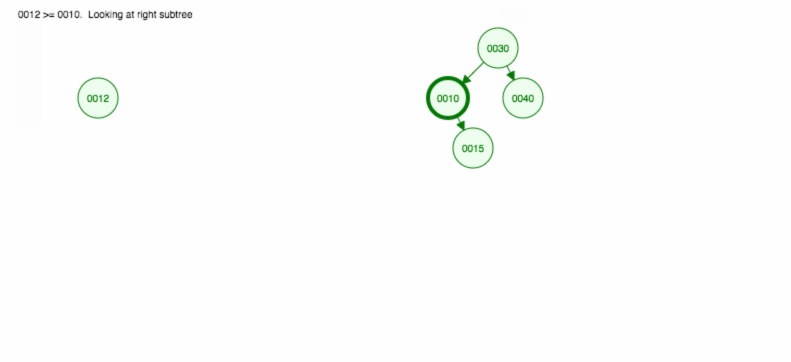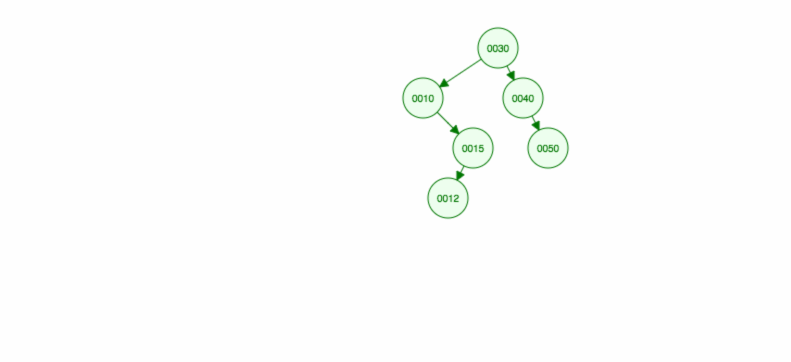
挿入は次のように実装できます。prototype.addFull Code

add(value) {
const newNode = new TreeNode(value);
if (this.root) {
const { found, parent } = this.findNodeAndParent(value);
if (found) { // duplicated: value already exist on the tree
found.meta.multiplicity = (found.meta.multiplicity || 1) + 1;
} else if (value < parent.value) {
parent.left = newNode;
} else {
parent.right = newNode;
}
} else {
this.root = newNode;
}
this.size += 1;
return newNode;
}

findNodeAndParentというヘルパー関数を使っている。もしそのノードがすでにツリーに存在していることがわかったら、multiplicityカウンターを増加させる。この関数がどのように実装されているか見てみましょう。

BinarySearchTree.prototype.findNodeAndParentFull Code

findNodeAndParent(value) {
let node = this.root;
let parent;
while (node) {
if (node.value === value) {
break;
}
parent = node;
node = ( value >= node.value) ? node.right : node.left;
}
return { found: node, parent };
}

findNodeAndParent が木を通過しながら値を検索していく様子を示しています。ルートから始まり (2行目)、値に基づいて左または右に移動します (10行目)。値がすでに存在する場合は、ノード found とその親を返す。ノードが存在しない場合でも、parentを返します。

BST ノードの削除

値の挿入と検索方法はわかりました。さて、次は削除操作を実装します。追加よりも少し難しいので、以下のケースで説明します。

リーフノード（子0個）の削除

 30 30
/ \ remove(12) / \
10 40 ---------> 10 40
\ / \ \ / \
15 35 50 15 35 50
/
12*

ノードの親（15）から参照を削除してnullとします。

 30 30
/ \ remove(10) / \
10* 40 ---------> 15 40
\ / \ / \
15 35 50 35 50

この場合、親（30）に行き、子（10）を子供の子供（15）に置き換えます。

2つの子を持つノードを削除する

 30 30
/ \ remove(40) / \
15 40* ---------> 15 50
/ \ /
35 50 35

2つの子 (35 と 50) を持っているノード40を削除するのです。親 (30) の子 (40) をその子の右の子 (50) に置き換えます。そして、左の子(35)を以前と同じ場所に保つので、50の左の子にする必要があります。

ノード40を削除する別の方法は、左の子(35)を上に移動し、右の子(50)を元の場所に維持することです。

二項探索木の性質を保つ限り、どちらの方法でもかまいません。 left < parent < right.

ルートの削除

 30* 50
/ \ remove(30) /
15 50 ---------> 35
/ /
35 15

ルート削除は先に述べた 0、1、2 子ノードの削除と非常に似ています。唯一の違いは、その後、ツリーのルートの参照を更新する必要があることです。

ここで、私たちが説明したことのアニメーションを示します。

どのように動作すべきかの良いアイデアが得られたので、それを実装してみましょう：

BinarySearchTree.prototype.BinarySearchTree (BSTree)。removeFull Code

remove(value) {
const nodeToRemove = this.find(value);
if (!nodeToRemove) return false;
// Combine left and right children into one subtree without nodeToRemove
const nodeToRemoveChildren = this.combineLeftIntoRightSubtree(nodeToRemove);
if (nodeToRemove.meta.multiplicity && nodeToRemove.meta.multiplicity > 1) {
nodeToRemove.meta.multiplicity -= 1; // handle duplicated
} else if (nodeToRemove === this.root) {
// Replace (root) node to delete with the combined subtree.
this.root = nodeToRemoveChildren;
this.root.parent = null; // clearing up old parent
} else {
const side = nodeToRemove.isParentLeftChild ? 'left' : 'right';
const { parent } = nodeToRemove; // get parent
// Replace node to delete with the combined subtree.
parent = nodeToRemoveChildren;
}
this.size -= 1;
return true;
}

以下は、実装のハイライトです：

最初に、ノードが存在するかどうかを検索します。
削除するノードが存在する場合、左と右の子を1つのサブツリーにまとめる。

削除するノードを組み合わせたサブツリーに置き換える。prototype.combineLeftIntoRightSubtreeFull Code

combineLeftIntoRightSubtree(node) {
if (node.right) {
const leftmost = this.getLeftmost(node.right);
leftmost.left = node.left;
return node.right;
}
return node.left;
}

例えば以下の木を結合したいとして、ノード30を削除しようとするとします。 30の左のサブツリーを右のサブツリーに混ぜたいのである。結果はこうなります:

 30* 40
/ \ / \
10 40 combine(30) 35 50
\ / \ -----------> /
15 35 50 10
\
15

新しいサブツリーをルートにしてしまうと、ノード30はもうないですね！(笑)

Binary Tree Transversal

二分木を走査する方法は、ノードを訪問する順序によって、in-order、pre-order、post-orderがある。

順方向探索

順方向探索は、左、親、右の順にノードを訪問する。inOrderTraversalFull Code

* inOrderTraversal(node = this.root) {
if (node.left) { yield* this.inOrderTraversal(node.left); }
yield node;
if (node.right) { yield* this.inOrderTraversal(node.right); }
}

この木を使って例を作ってみることにする。

順にトラバースすると次の値が出力されます。 3, 4, 5, 10, 15, 30, 40. もしツリーが BST であれば、ノードはこの例のように昇順にソートされます。

後置走査

後置走査では、左、右、親の順でノードを訪問します。

BinarySearchTree.prototype.postOrderTraversalFull Code

* postOrderTraversal(node = this.root) {
if (node.left) { yield* this.postOrderTraversal(node.left); }
if (node.right) { yield* this.postOrderTraversal(node.right); }
yield node;
}

Post-order traversalは次の値を出力するだろう。 3, 4, 5, 15, 40, 30, 10.

Pre-Order Traversal and DFS

Pre-order traversal visit nodes on this order: parent, left, right.

BinarySearchTree.DFS Pre-order Traversal and DFS Pre-order Traversal on this order: parent, left, right.prototype.preOrderTraversalFull Code

* preOrderTraversal(node = this.root) {
yield node;
if (node.left) { yield* this.preOrderTraversal(node.left); }
if (node.right) { yield* this.preOrderTraversal(node.right); }
}

Pre-order traversalは次の値を出力します。 10, 5, 4, 3, 30, 15, 40. この数字の並びは、深さ優先探索（DFS）を実行した場合と同じ結果です。

BinarySearchTree.prototype.dfsFull Code

* dfs() {
const stack = new Stack();
stack.add(this.root);
while (!stack.isEmpty()) {
const node = stack.remove();
yield node;
// reverse array, so left gets removed before right
node.descendants.reverse().forEach(child => stack.add(child));
}
}

DFS について復習が必要なら Graph ポストで詳しく取り上げています。

Breadth-First Search (BFS)

DFS と同様に、Stack を Queue で置き換えることにより、BFS を実装できます:

BinarySearchTree.BFS (バイナリサーチツリー、BinarySearchTree.BFS)prototype.bfsFull Code

* bfs() {
const queue = new Queue();
queue.add(this.root);
while (!queue.isEmpty()) {
const node = queue.remove();
yield node;
node.descendants.forEach(child => queue.add(child));
}
}

BFSの順番は。 10, 5, 30, 4, 15, 40, 3

Balanced vs. Non-balanced Trees

ここまで、add, remove, find要素の扱いについて述べてきました。しかし、実行時間については話していない。

例えば、数字を昇順に足したいとします。

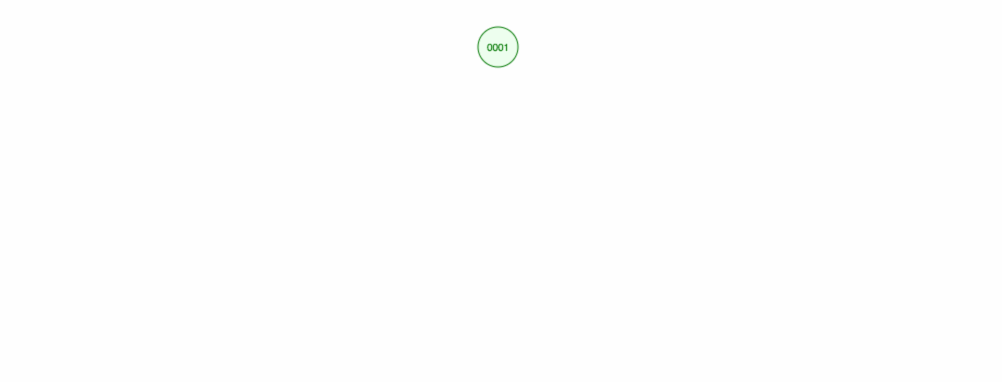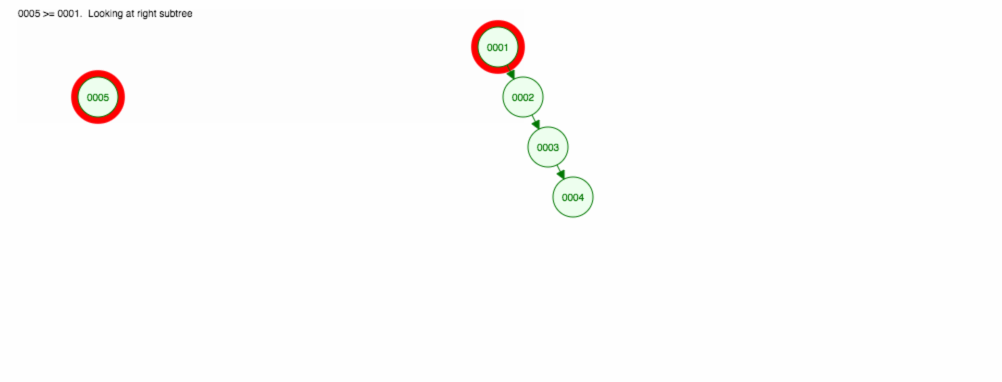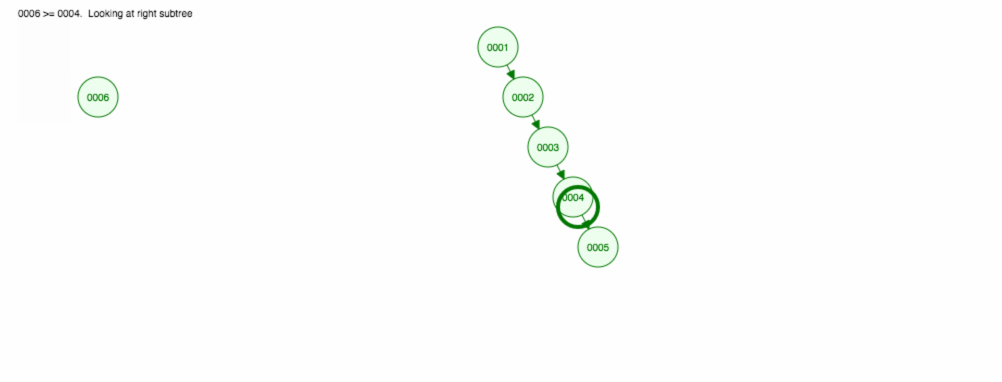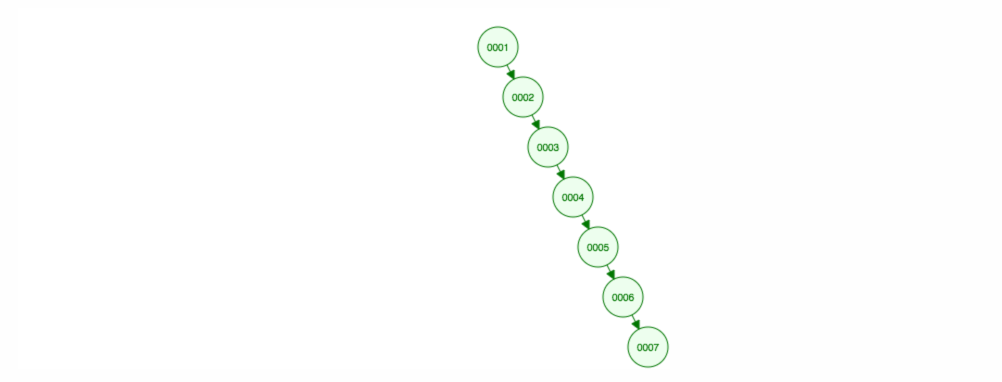
結局、すべてのノードを右側に置くことになります! このアンバランスな木は LinkedList と変わらないので、要素を見つけるには O(n) が必要です。 😱

アンバランスなツリーで何かを探すのは、辞書の単語を 1 ページずつ探すようなものです。木がバランスしていると、辞書を真ん中で開くことができ、そこからアルファベットと探している単語に応じて、左か右に行かなければならないかわかる。

木をバランスする方法を見つける必要がある！

木がバランスしていたら、各ノードを通過する代わりに O(log n) で要素を見つけることができるだろう。

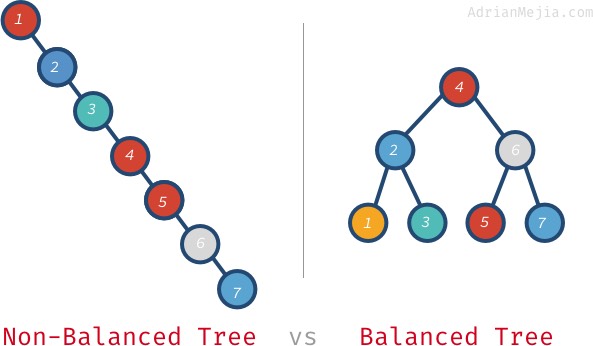
バランスのとれていない木で7を探すと、1から7まで行かなければなりません。しかし、バランスのとれた木では、訪問します。 4, 6, 7となる。さらに大きな木になると、さらに悪化する。 100万個のノードがある場合、存在しない要素を探すには100万個全部を訪問する必要があるかもしれません。それが 20 回で済むのです! これは大きな違いです。

次回の投稿では、自己バランスツリー (AVL ツリー) を使用してこの問題を解決します。

まとめ

私たちはツリーについて多くの領域をカバーしました。

木は、ノードが 0 以上の子孫/子供を持つデータ構造です。
木のノードにはサイクルがありません（非循環的）。サイクルを持つ場合、それは代わりにGraphデータ構造である。
子ノードが2つ以下のツリーをこう呼ぶ。バイナリツリー
バイナリツリーを左の値が親より小さく、右の子が大きくなるようにソートすると、バイナリサーチツリーになる。
ツリーを前/後/順に訪問できる。 🤦🏻
A balanced の時間複雑度は O(log n)である。 🎉

Adrian Mejia

Adrian Mejia

admin, Author

木：基本概念

簡単な木データ構造の実装

Binary Trees

完全、完全、および完全なバイナリツリー

二項探索木 (BST)

BST Implementation

BST ノード挿入

BST ノードの削除

Binary Tree Transversal

Balanced vs. Non-balanced Trees

まとめ

コメントを残すコメントをキャンセル

admin, Author

木：基本概念

簡単な木データ構造の実装

Binary Trees

完全、完全、および完全なバイナリ ツリー

二項探索木 (BST)

BST Implementation

BST ノード挿入

BST ノードの削除

Binary Tree Transversal

Balanced vs. Non-balanced Trees

まとめ

コメントを残す コメントをキャンセル

完全、完全、および完全なバイナリツリー

コメントを残すコメントをキャンセル