Tree data structures have many uses, and it’s good to have a basic understanding of how they work. As árvores são a base para outras estruturas de dados muito utilizadas, como Mapas e Conjuntos. Também são usadas em bancos de dados para realizar buscas rápidas. O HTML DOM usa uma estrutura de dados em árvore para representar a hierarquia dos elementos. Este post irá explorar os diferentes tipos de árvores como árvores binárias, árvores de busca binária, e como implementá-las.

Nós exploramos estruturas de dados gráficos no post anterior, que são um caso generalizado de árvores. Vamos começar a aprender o que são estruturas de dados de árvores!

Este post é parte de uma série tutorial:

Estruturas de Dados de Aprendizagem e Algoritmos (DSA) para Iniciantes

1. Intro to algorithm’s time complexity and Big O notation

2. Eight time complexities that every programmer should know

3. Data Structures for Beginners: Arrays, HashMaps e Listas

4. Estruturas de Dados Gráficos para Iniciantes

5. Estruturas de Dados Gráficos para Iniciantes 👈 você está aqui

6. Árvores de Busca Binária Auto-equilibradas

7. Anexo I: Análise de Algoritmos Recursivos

Árvores: conceitos básicos

Uma árvore é uma estrutura de dados onde um nó pode ter zero ou mais filhos. Cada nó contém um valor. Como nos gráficos, a conexão entre nós é chamada de arestas. Uma árvore é um tipo de gráfico, mas nem todos os gráficos são árvores (mais sobre isso depois).

Estas estruturas de dados são chamadas de “árvores” porque a estrutura de dados se assemelha a uma árvore 🌳. Ela começa com um nó raiz e ramifica com seus descendentes, e finalmente, há folhas.

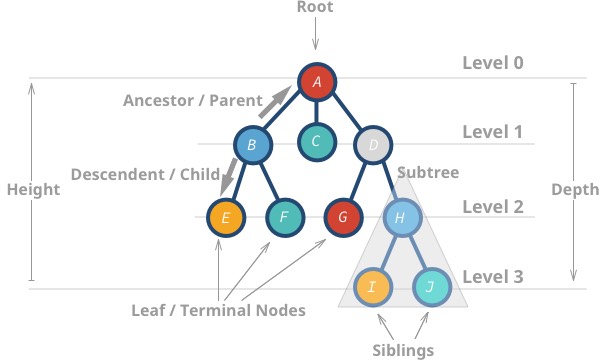
Aqui estão algumas propriedades das árvores:

• O nó mais alto chama-se raiz.
• Um nó sem filhos chama-se nó folha ou nó terminal.
• Altura (h) da árvore é a distância (contagem de bordas) entre a folha mais distante até a raiz.
  • A tem uma altura de 3
  • I tem uma altura de 0
• Profundidade ou nível de um nó é a distância entre a raiz e o nó em questão.
  • H tem uma profundidade de 2
  • B tem uma profundidade de 1

Implementando uma estrutura de dados em árvore simples

Como vimos anteriormente, um nó de árvore é apenas uma estrutura de dados com um valor e links para os seus descendentes.

Aqui está um exemplo de um nó de árvore:

1
2
3
4
5
6

class TreeNode {
constructor(value) {
this.value = value;
this.descendants = ;
}
}

Podemos criar uma árvore com 3 descendentes como se segue:

1
2
3
4
5
6
7
8
9
10

// create nodes with values
const abe = new TreeNode('Abe');
const homer = new TreeNode('Homer');
const bart = new TreeNode('Bart');
const lisa = new TreeNode('Lisa');
const maggie = new TreeNode('Maggie');
// associate root with is descendants
abe.descendants.push(homer);
homer.descendants.push(bart, lisa, maggie);

É tudo; nós temos uma estrutura de dados em árvore!

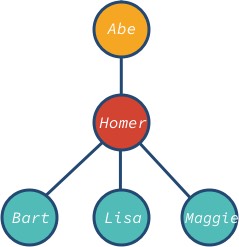
O nó abe é a raiz e bart, lisa e maggie são os nós foliares da árvore. Note que o nó da árvore pode ter diferentes descendentes: 0, 1, 3, ou qualquer outro valor.

As estruturas de dados da árvore têm muitas aplicações como:

• Maps
• Sets
• Bases de dados
• Priority Queues
• Querying an LDAP (Lightweight Directory Access Protocol)
• Representar o Document Object Model (DOM) para HTML em Websites.

Árvores binárias

Nós de árvores podem ter zero ou mais filhos. Entretanto, quando uma árvore tem no máximo dois filhos, então ela é chamada de árvore binária.

Árvores binárias completas, completas e perfeitas

Dependente de como os nós estão dispostos em uma árvore binária, ela pode ser completa, completa e perfeita:

• Árvore binária completa: cada nó tem exatamente 0 ou 2 filhos (mas nunca 1).
• Árvore binária completa: quando todos os níveis excepto o último estão cheios de nós.
• Árvore binária perfeita: quando todos os níveis (incluindo o último) estão cheios de nós.

Vejam estes exemplos:

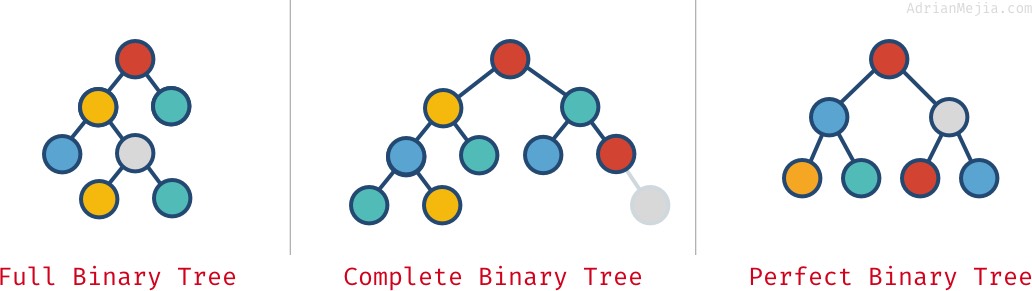
Estas propriedades nem sempre são mutuamente exclusivas. Você pode ter mais de um:

• Uma árvore perfeita está sempre completa e cheia.
  • Árvores binárias perfeitas têm precisamente `2^k – 1` nós, onde k é o último nível da árvore (começando com 1).
• Uma árvore completa nem sempre é full.
  • Tal como no nosso exemplo “completo”, uma vez que tem um pai com apenas um filho. Se removermos o nó cinza mais à direita, então teremos uma árvore completa e completa mas não perfeita.
• Uma árvore completa nem sempre é completa e perfeita.

Árvore de Busca Binária (BST)

Árvores de Busca Binária ou BST para abreviar são uma aplicação particular de árvores binárias. BST tem no máximo dois nós (como todas as árvores binárias). Entretanto, os valores são para que o valor da criança esquerda seja menor que o do pai, e a criança direita seja maior.

Duplicatas: Alguns BST não permitem duplicatas enquanto outros adicionam os mesmos valores que uma criança direita. Outras implementações podem manter uma contagem em um caso de duplicidade (vamos fazer esta mais tarde).

Passemos a implementar uma árvore de busca binária!

Implementação BST

BST são muito semelhantes à nossa implementação anterior de uma árvore. No entanto, existem algumas diferenças:

• Os nós podem ter, no máximo, duas crianças: esquerda e direita.
• Os valores dos nós têm de ser ordenados como left < parent < right.

Aqui está o nó de árvore. Muito semelhante ao que fizemos antes, mas adicionamos alguns getters e setters úteis para crianças da esquerda e da direita. Note também que mantemos uma referência aos pais, e a atualizamos toda vez que adicionamos crianças.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32

const LEFT = 0;
const RIGHT = 1;
class TreeNode {
constructor(value) {
this.value = value;
this.descendants = ;
this.parent = null;
}
get left() {
return this.descendants;
}
set left(node) {
this.descendants = node;
if (node) {
node.parent = this;
}
}
get right() {
return this.descendants;
}
set right(node) {
this.descendants = node;
if (node) {
node.parent = this;
}
}
}

Ok, até agora, podemos adicionar uma criança esquerda e direita. Agora, vamos fazer a classe BST que impõe a left < parent < right regra.

1
2
3
4
5
6
7
8
9
10
11
12
13

class BinarySearchTree {
constructor() {
this.root = null;
this.size = 0;
}
add(value) { /* ... */ }
find(value) { /* ... */ }
remove(value) { /* ... */ }
getMax() { /* ... */ }
getMin() { /* ... */ }
}

Sigamos a inserção de implementação.

Inserção do nó BST

Para inserir um nó em uma árvore binária, fazemos o seguinte:

1. Se uma árvore estiver vazia, o primeiro nó se torna a raiz, e você está feito.
2. Comparar o valor da raiz/parente se for mais alto vá para a direita, se for mais baixo vá para a esquerda. Se for o mesmo, então o valor já existe para que você possa aumentar a contagem de duplicatas (multiplicidade).
3. Repetir #2 até encontrarmos um espaço vazio para inserir o novo nó.

Vamos fazer uma ilustração de como inserir 30, 40, 10, 15, 12, 50:

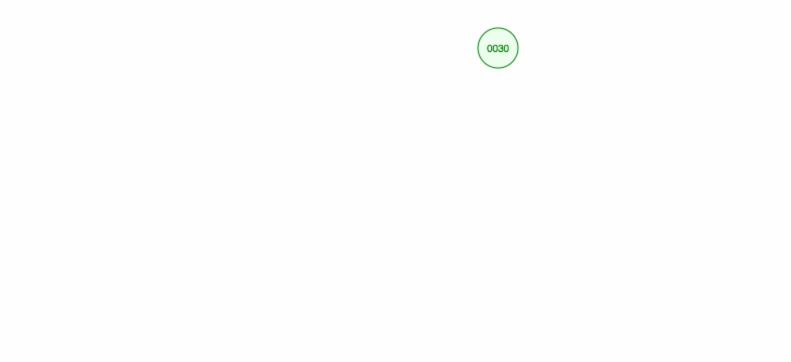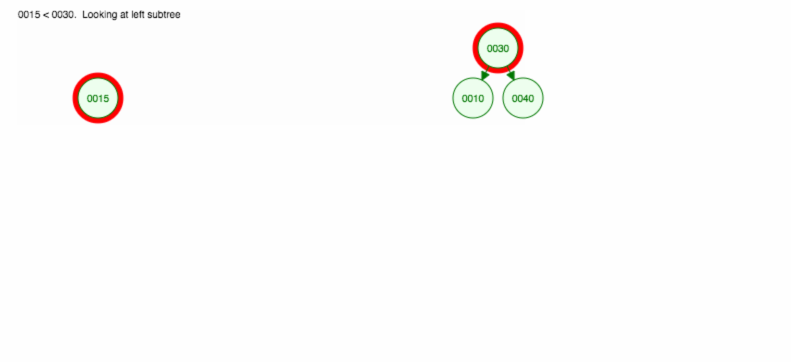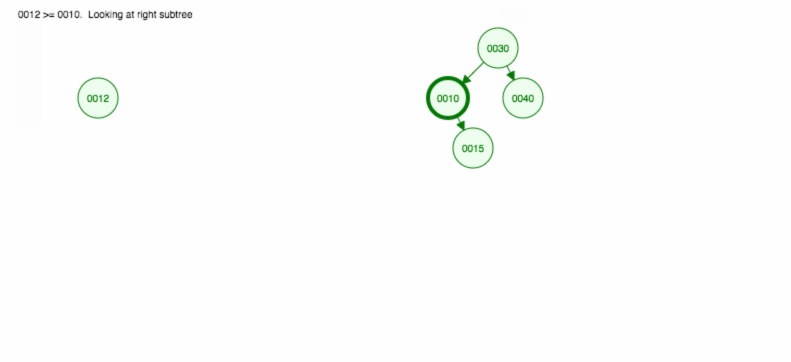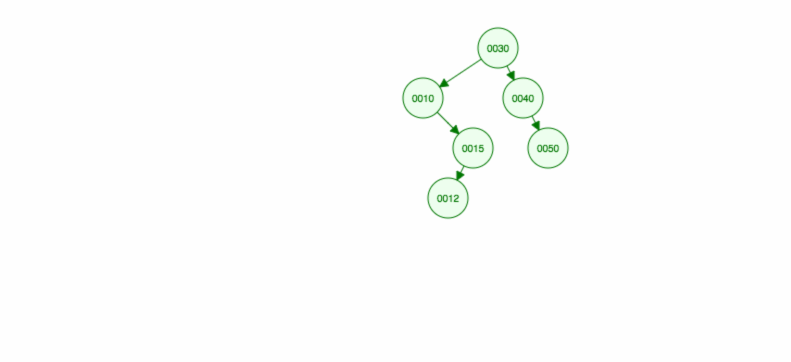
Podemos implementar a inserção da seguinte forma:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19

add(value) {
const newNode = new TreeNode(value);
if (this.root) {
const { found, parent } = this.findNodeAndParent(value);
if (found) { // duplicated: value already exist on the tree
found.meta.multiplicity = (found.meta.multiplicity || 1) + 1;
} else if (value < parent.value) {
parent.left = newNode;
} else {
parent.right = newNode;
}
} else {
this.root = newNode;
}
this.size += 1;
return newNode;
}

Usamos uma função de ajuda chamada findNodeAndParent. Se descobrirmos que o nó já existe na árvore, então aumentamos o contador multiplicity. Vamos ver como esta função é implementada:

1
2
3
4
5
6
7
8
9
10
11
12
13
14

findNodeAndParent(value) {
let node = this.root;
let parent;
while (node) {
if (node.value === value) {
break;
}
parent = node;
node = ( value >= node.value) ? node.right : node.left;
}
return { found: node, parent };
}

findNodeAndParent passa através da árvore, procurando o valor. Ele começa na raiz (linha 2) e depois vai para a esquerda ou direita com base no valor (linha 10). Se o valor já existir, ele retornará o nó found e também o pai. Caso o nó não exista, ainda retornaremos o valor parent.

BST Node Deletion

Sabemos inserir e procurar por valor. Agora, vamos implementar a operação de apagar. É um pouco mais complicado do que adicionar, então vamos explicar com os seguintes casos:

Apagar um nó de folha (0 filhos)

1
2
3
4
5
6
7

 30 30
/ \ remove(12) / \
10 40 ---------> 10 40
\ / \ \ / \
15 35 50 15 35 50
/
12*

Retiramos a referência do pai do nó (15) para ser nula.

Apagar um nó com um filho.

1
2
3
4
5

 30 30
/ \ remove(10) / \
10* 40 ---------> 15 40
\ / \ / \
15 35 50 35 50

Neste caso, vamos ao pai (30) e substituímos a criança (10) por uma criança (15).

Apagar um nó com duas crianças

1
2
3
4
5

 30 30
/ \ remove(40) / \
15 40* ---------> 15 50
/ \ /
35 50 35

Estamos a remover o nó 40, que tem duas crianças (35 e 50). Substituímos o filho do pai (30) (40) pelo filho direito da criança (50). Depois mantemos a criança esquerda (35) no mesmo lugar antes, então temos que fazer dela a criança esquerda de 50,

Outra maneira de remover o nó 40 é mover a criança esquerda (35) para cima e depois manter a criança direita (50) onde ela estava.

1
2
3
4
5

 30
/ \
15 35
\
50

De qualquer maneira está bem desde que se mantenha a propriedade da árvore de busca binária: left < parent < right.

Eliminar a raiz.

1
2
3
4
5

 30* 50
/ \ remove(30) /
15 50 ---------> 35
/ /
35 15

Eliminar a raiz é muito semelhante à remoção de nós com 0, 1 ou 2 crianças discutidas anteriormente. A única diferença é que depois precisamos atualizar a referência da raiz da árvore.

Aqui está uma animação do que discutimos.

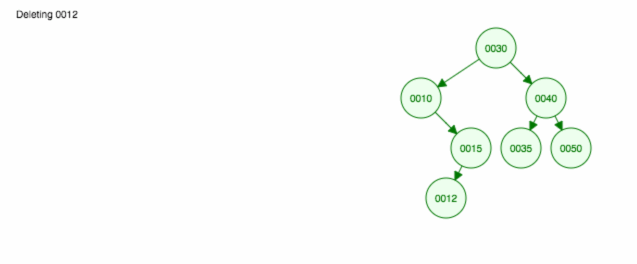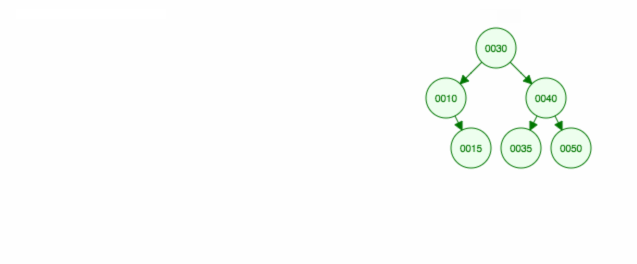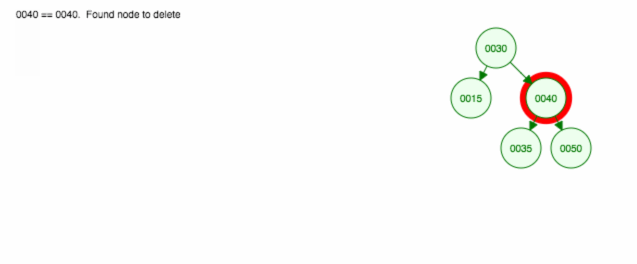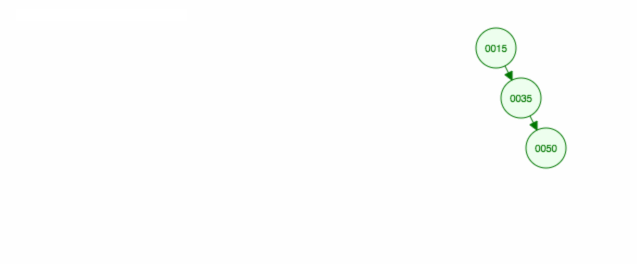
A animação sobe a criança/sub-árvore esquerda e mantém a criança/sub-árvore direita no lugar.

Agora temos uma boa ideia de como deve funcionar, vamos implementá-la:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23

remove(value) {
const nodeToRemove = this.find(value);
if (!nodeToRemove) return false;
// Combine left and right children into one subtree without nodeToRemove
const nodeToRemoveChildren = this.combineLeftIntoRightSubtree(nodeToRemove);
if (nodeToRemove.meta.multiplicity && nodeToRemove.meta.multiplicity > 1) {
nodeToRemove.meta.multiplicity -= 1; // handle duplicated
} else if (nodeToRemove === this.root) {
// Replace (root) node to delete with the combined subtree.
this.root = nodeToRemoveChildren;
this.root.parent = null; // clearing up old parent
} else {
const side = nodeToRemove.isParentLeftChild ? 'left' : 'right';
const { parent } = nodeToRemove; // get parent
// Replace node to delete with the combined subtree.
parent = nodeToRemoveChildren;
}
this.size -= 1;
return true;
}

Aqui estão alguns destaques da implementação:

• Primeiro, procuramos se o nó existe. Se não existir, retornamos falsos, e pronto!
• Se o nó a ser removido existir, então combine as crianças esquerda e direita em uma sub-árvore.
• Substitua o nó a ser removido pela sub-árvore combinada.

A função que combina a esquerda na sub-árvore direita é a seguinte:

1
2
3
4
5
6
7
8

combineLeftIntoRightSubtree(node) {
if (node.right) {
const leftmost = this.getLeftmost(node.right);
leftmost.left = node.left;
return node.right;
}
return node.left;
}

Por exemplo, digamos que queremos combinar a seguinte árvore, e estamos prestes a apagar o nó 30. Queremos misturar a sub-árvore esquerda da década de 30 na direita. O resultado é este:

1
2
3
4
5
6
7

 30* 40
/ \ / \
10 40 combine(30) 35 50
\ / \ -----------> /
15 35 50 10
\
15

Se fizermos da nova sub-árvore a raiz, então o nó 30 já não é mais!

Transversal da árvore binária

Existem diferentes formas de atravessar uma árvore binária, dependendo da ordem em que os nós são visitados: em ordem, pré-ordem e pós-ordem. Também podemos usar os nósDFS eBFS que aprendemos no post do gráfico. Vamos percorrer cada um deles.

>

Na-Order Traversal

>

Na-order traversal visitam os nós nesta ordem: esquerda, pai, direita.

>

1
2
3
4
5

* inOrderTraversal(node = this.root) {
if (node.left) { yield* this.inOrderTraversal(node.left); }
yield node;
if (node.right) { yield* this.inOrderTraversal(node.right); }
}

Vamos usar esta árvore para fazer o exemplo:

1
2
3
4
5
6
7

 10
/ \
5 30
/ / \
4 15 40
/
3

A travessia por ordem imprimiria os seguintes valores: 3, 4, 5, 10, 15, 30, 40. Se a árvore é um BST, então os nós serão ordenados em ordem ascendente como no nosso exemplo.

Pós-ordem Traversal

Pós-ordem Traversal visitar nós nesta ordem: esquerda, direita, pai.

1
2
3
4
5

* postOrderTraversal(node = this.root) {
if (node.left) { yield* this.postOrderTraversal(node.left); }
if (node.right) { yield* this.postOrderTraversal(node.right); }
yield node;
}

Pós-ordem de travessia imprimiria os seguintes valores: 3, 4, 5, 15, 40, 30, 10.

Pré-ordem Traversal e DFS

Pré-ordem de nós de visita transversal nesta ordem: pai, esquerda, direita.

1
2
3
4
5

* preOrderTraversal(node = this.root) {
yield node;
if (node.left) { yield* this.preOrderTraversal(node.left); }
if (node.right) { yield* this.preOrderTraversal(node.right); }
}

Pré-ordem de travessia imprimiria os seguintes valores: 10, 5, 4, 3, 30, 15, 40. Esta ordem de números é o mesmo resultado que obteríamos se executássemos a Pesquisa de Profundidade-Primeiro (DFS).

1
2
3
4
5
6
7
8
9
10
11
12

* dfs() {
const stack = new Stack();
stack.add(this.root);
while (!stack.isEmpty()) {
const node = stack.remove();
yield node;
// reverse array, so left gets removed before right
node.descendants.reverse().forEach(child => stack.add(child));
}
}

Se precisar de uma actualização na DFS, nós cobrimo-la em detalhe no post Graph.

Breadth-First Search (BFS)

Similiar à DFS, podemos implementar uma BFS trocando a Stack por uma Queue:

1
2
3
4
5
6
7
8
9
10
11

* bfs() {
const queue = new Queue();
queue.add(this.root);
while (!queue.isEmpty()) {
const node = queue.remove();
yield node;
node.descendants.forEach(child => queue.add(child));
}
}

A ordem BFS é: 10, 5, 30, 4, 15, 40, 3

Árvores Equilibradas vs. Não Equilibradas

Até agora, discutimos como add, remove, e find elementos. No entanto, não temos falado sobre os tempos de execução. Vamos pensar nos piores cenários.

Vamos dizer que queremos adicionar números em ordem ascendente.

>

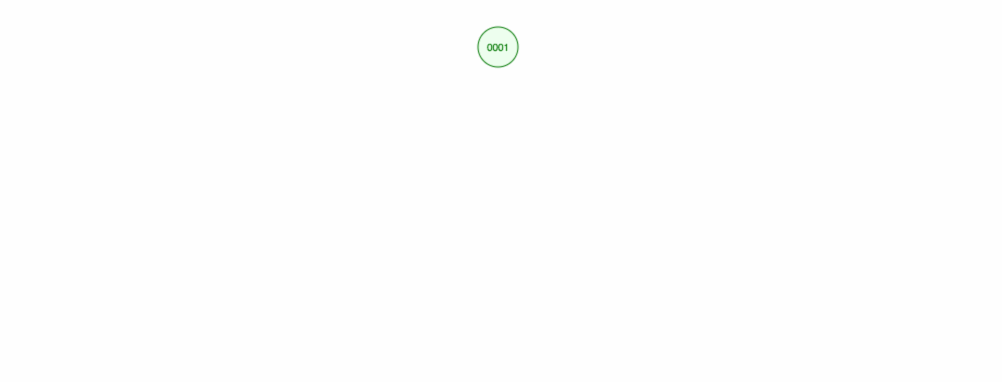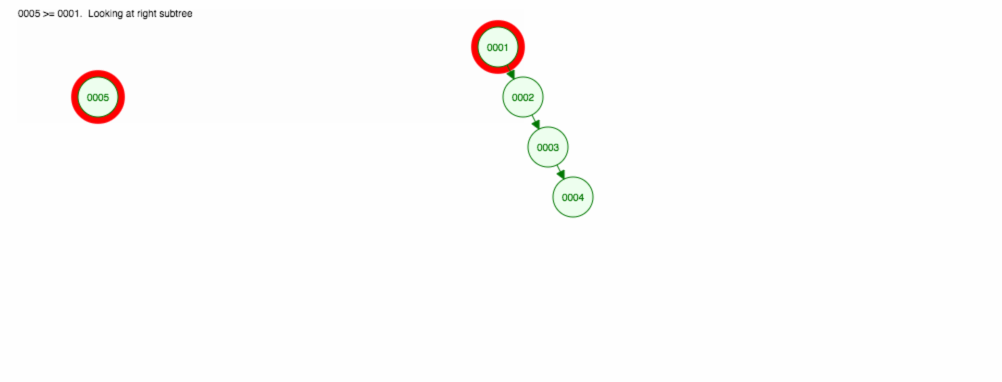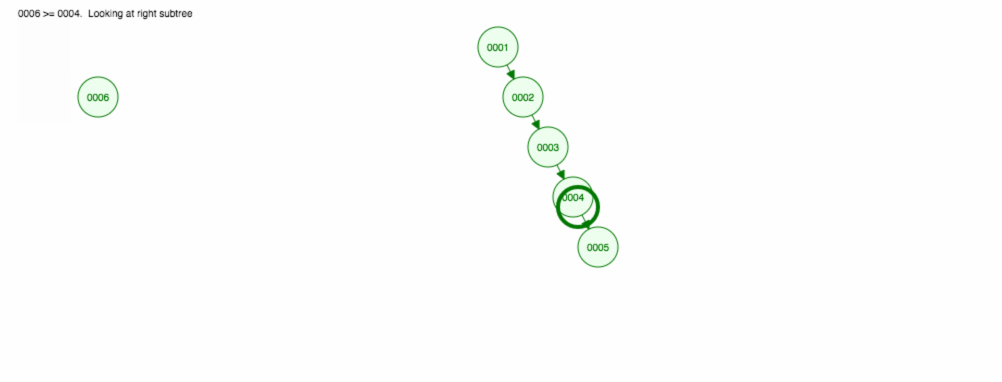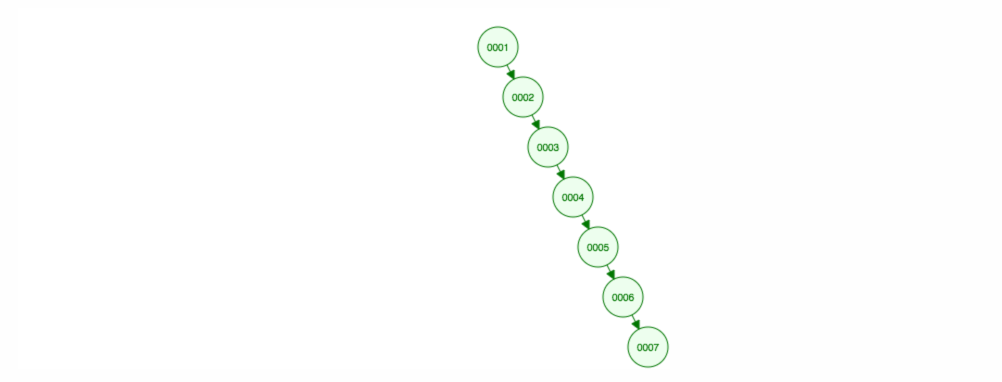Acabaremos com todos os nós do lado direito! Esta árvore desequilibrada não é melhor do que uma LinkedList, então encontrar um elemento levaria O(n). 😱

Procurar algo em uma árvore desequilibrada é como procurar uma palavra no dicionário página por página. Quando a árvore está equilibrada, você pode abrir o dicionário no meio, e de lá, você sabe se você tem que ir para a esquerda ou direita dependendo do alfabeto e da palavra que você está procurando.

Precisamos encontrar uma maneira de equilibrar a árvore!

Se a árvore estivesse equilibrada, poderíamos encontrar elementos em O(log n) ao invés de passar por cada nó. Vamos falar sobre o que significa uma árvore balanceada.

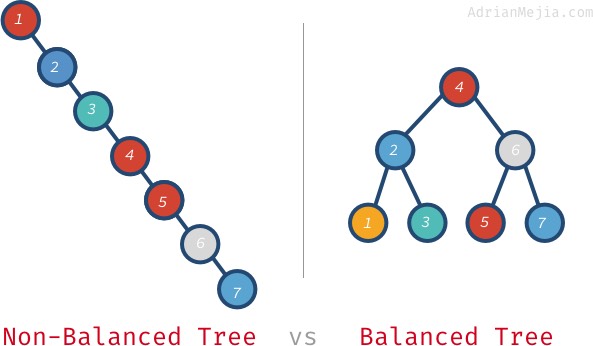
Se procurarmos por 7 na árvore não balanceada, temos que ir de 1 a 7. No entanto, na árvore balanceada, nós visitamos: 4, 6, e 7. E fica ainda pior com árvores maiores. Se você tiver um milhão de nós, a busca por um elemento inexistente pode exigir que você visite todos os milhões enquanto estiver em uma árvore balanceada. Só precisa de 20 visitas! Essa é uma diferença enorme!

Vamos resolver esse problema no próximo post usando árvores auto-equilibradas (árvores AVL).

Resumo

Cobrimos muito terreno para árvores. Vamos resumir com balas:

• A árvore é uma estrutura de dados onde um nó tem 0 ou mais descendentes/filhos.
• Nós de árvores não têm ciclos (acíclicos). Se ele tiver ciclos, é uma estrutura de dados Gráficos em vez disso.
• Árvores com dois filhos ou menos são chamadas: Árvore binária
• Quando uma árvore binária é classificada de forma que o valor esquerdo seja menor que o pai e o filho direito seja maior, então e só então temos uma árvore de busca binária.
• Pode visitar uma árvore de forma pré/pós/ordem.
• Um desequilibrado tem uma complexidade de tempo de O(n). 🤦🏻
• Um desequilibrado tem uma complexidade de tempo de O(log n). 🎉