Fysisk kemi er et ret bredt emne; det dækker:

• Kvantumkemi
• Thermokemi (gennemgang + mere)
• Kinetik (gennemgang + mere)
• Statistisk mekanik

Da der er ret mange emner til et svar, vil jeg kun give to eksempler pr. emne. Dette bliver et langt svar, men du kan fokusere på det, du leder efter.

KVANTUMKEMI

Kvantumkemi handler generelt om at forsøge at forstå scenarier på den picoskopiske skala, at modellere systemer i bekvemme matematiske repræsentationer og foretage de relevante tilnærmelser.

To eksempler på kvantekemi er:

• Simpel harmonisk oscillator (to kugler forbundet af en ideel fjeder)

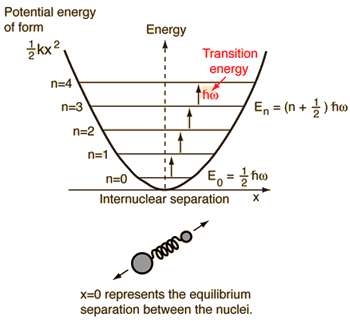
For dette system, som vi kender fra fysikken, reducerer vi det fra et klassisk problem med to legemer til et problem med et legeme med relative koordinater og en reduceret masse, #mu = (m_1m_2)/(m_1 + m_2)#.

Dette system fokuserer på at forstå den elastiske potentielle energi i den molekylære binding.

• Stiv rotor (to kugler forbundet med en stang, dvs. 100% stiv fjeder)

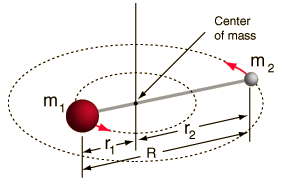
Dette system er en forenkling, da alle molekyler har en eller anden form for udstrækning/vibration af bindinger (du ville forstå, hvorfor denne forenkling er OK, hvis du så matematikken!).

Det giver os imidlertid mulighed for at dekomponere denne vinkelkomponent af et tolegemesystem og forstå molekylets rotationsegenskaber.

THERMOKEMI

Dette ser på den makroskopiske skala for varmestrømning, arbejde, frie energier og så videre. Du har gjort det før i almen kemi noget, og det gennemgås og uddybes.

To eksempler er:

• Bestemmelse af termodynamiske værdier ud fra målbare størrelser

Hvad er kemi, hvis det ikke er praktisk?

Så et fælles tema er at kunne foretage afledninger og udtrykke de vigtigste termodynamiske størrelser (entropi, enthalpi, Gibbs + Helmholtz’ frie energi, intern energi) i form af naturlige variabler som volumen, temperatur og tryk.

F.eks. kan man beregne entropien ud fra en isotermisk ekspansion (#DeltaT = 0, DeltaV > 0#) ved at kende #V_2# og #V_1#, eller #P_2# og #P_1#, og det for en monatomisk idealgas:

##DeltaS = -nRln(P_2/P_1) = nRln(V_2/V_1)#

• Ideal og ikke-ideal ikke-elektrolyt/elektrolytopløsninger

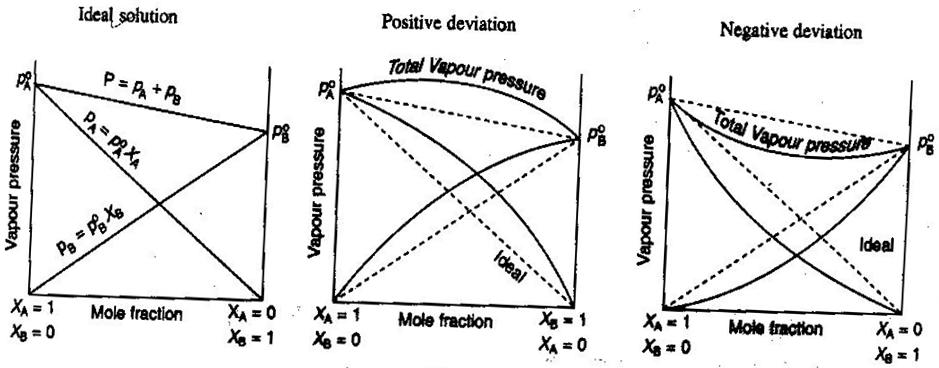
I almen kemi, vil vi gerne behandle opløsninger ideelt, således at volumener er additive, koncentrationer af stærke elektrolytter er lige #”mol/L “#beregninger og så videre. Nogle måder, hvorpå opløsninger måske ikke er ideelle:

• Løsningen kan udvide sig eller trække sig sammen, efter at den er blevet blandet.
• Ionparring mindsker opløsningens ionstyrke og reducerer van’t Hoff-faktoren #i# for den opløste stofmængde.
• Den opløstes tendens til at undslippe ændrer dens effektive koncentration (dens aktivitet).

KINETIK

Du har måske prøvet dette før i et almindeligt kemikursus eller måske i gymnasiet. Fysisk kemi uddyber dette lidt mere ved at se nærmere på reaktionsmekanismer og gasfasedynamik.

To eksempler:

• Steady-State-approximation

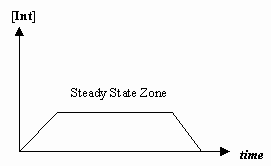
I nogle tilfælde er hastigheden af det første mekanistiske trin meget langsommere end hastigheden af det andet trin, og vi approksimerer, at koncentrationen af mellemproduktet reelt ikke ændrer sig (#(d)/(dt) = 0#).

Det giver mulighed for at udlede en hastighedslov, der er specifik for en mekanisme, og for at vi kan udtrykke en “observeret hastighedskonstant” i form af hastighedskonstanterne for de enkelte trin.

• Reelle gaslove

Du er måske blevet præsenteret for van der Waals-tilstandsligningen:

#(V – nb) = nRT#

Jamen, der er nogle andre, som Redlich-Kwong, Peng-Robinson osv.

Den grundlæggende idé er, at de alle fungerer bedre for visse gasser end andre, men de fungerer alle for at tage højde for gassernes reelle egenskaber i stedet for at antage, at alle er en elastisk kolliderende inert punktmasse.

STATISTISK MÆKANIK

Med statistisk mekanik tager vi et skridt tilbage og ser på den picoskopiske verden fra et makroskopisk perspektiv:

“Hvad kan vi lære af et system, hvis vi tænker som en kvantekemiker om en stor samling af partikler?”

To eksempler:

• Equipartitionssætning

#<< K >> = N/2nRT = N/2 k_BT#,

hvor #N# er antallet af frihedsgrader for hver type bevægelse (lineær, roterende, vibrationel, elektronisk, nuklear). Grundlæggende tages der hensyn til alle bevægelsestyper i et molekyle for at estimere dets gennemsnitlige kinetiske energi, #<< K >>#.

Dette virker kun ved “høje nok” temperaturer. Normalt er det OK for translations- og rotationsbevægelser, men det har en tendens til at overvurdere vibrationsbidrag.

• Den mikrokanoniske partitionsfunktion

#q = sum_(i=1)^(N) g_ie^(-beta epsilon_i)#,

hvor:

• #g_i# er degenerationen for tilstand #i# med energi #epsilon_i#.
• #N# er det samlede antal tilstande, der er til rådighed.

Ligesom bølgefunktionen #psi# angiver alt, hvad der er at vide om et kvantemekanisk system, angiver den mikrokanoniske fordelingsfunktion, hvordan et molekyle kan fordele sin tilgængelige energi på de mulige typer af tilstande (translations-, rotations-, vibrations-, elektroniske og nukleare).

Der findes en #q# for hver tilstandstype: #q_(tr)#, #q_(rot)#, #q_(vib)#, #q_(el ec)# og #q_(n uc)#.

Fra kendskabet til hver type #q# kan de velkendte termodynamiske størrelser, såsom entropi (#S#), enthalpi (#H#), Gibbs’ frie energi (#G#) osv. udledes i termer af hver type #q#.

Som et nyttigt eksempel kan den absolutte molekylære entropi ved ALLE temperaturer i de fleste tilfælde beregnes som:

#S/N = k_B ln (q/N)_”tot” + (<< epsilon >>_”tot”)/T + k_B#,

hvor:

• #k_B ~~ “0.695 cm”^(-1)”/K “# er Boltzmann-konstanten.
• #(q/N)_”tot” = (q_(tr))/Nq_(rot)q_(vib)q_(el ec)q_(n uc)# er den samlede mikrokanoniske fordelingsfunktion, der omfatter alle de mulige tilstandstyper, og #N# er det samlede antal betragtede molekyler.
• #<< epsilon >> = E/N# er den molekylære energi, der er defineret som #<<< epsilon >> = k_BT^2((del ln (q”/”N)_”tot”)/(del T))_V#.

(Ja, denne formel ved #”298,15 K “# gør det muligt at beregne den samme #S^@#, som du ser i dit lærebogsbilag!)

Et eksempel på denne formel i brug kan findes her.