Physical Chemistry はやや広いトピックで、次のようなものを扱います:
- Quantum chemistry
- Thermochemistry (Review + More)
- Kinetics (Review + More)
- Statistical mechanics
一つの答えに対してかなりの数の話題がありますので、一つの話題について二つの例のみを提示することにしましょう。 長い回答になりそうですが、何を求めているのかを絞ってください。
QUANTUM CHEMISTRY
量子化学は一般に、ピコスコピックスケールでシナリオを理解しようとし、システムを便利な数学表現でモデル化して適切な近似を行うことである。
量子化学の例としては、次のようなものがあります。
- 単純調和振動子(理想バネでつながった2つの球)
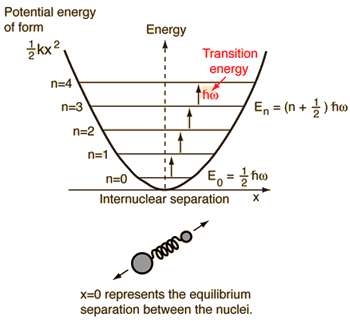
物理で知っているこの系に対して、2体古典問題から、相対座標と質量が減った1体問題、#mu = (m_1m_2)/(m_1 + m_2)# に還元するのである。
このシステムは、分子結合の弾性ポテンシャルエネルギーの理解に重点を置いています。
- リジッドローター(2つの球を棒でつないだもの、つまり100%硬いバネ)
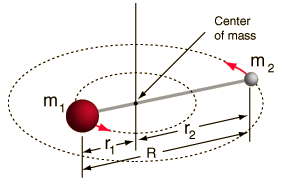
すべての分子には何らかの結合伸び・振動があるのでこのシステムは単純化しています(なぜこの単純化でもいいかは数学を見れば理解できるでしょう!)。
しかし、2 体系のこの角度成分を分解し、分子の回転特性を理解することができます。
THERMOCHEMISTRY
これは、熱流、仕事、自由エネルギーなどのマクロなスケールを調べます。 一般化学でなんとなくやったことがあると思いますが、これを復習して発展させたものです。
二つの例:
- 測定可能な量から熱力学値を求める
実用でなければ化学とは何でしょう?
そこで共通するテーマは、主要な熱力学量(エントロピー、エンタルピー、ギブス+ヘルムホルツ自由エネルギー、内部エネルギー)を体積、温度、圧力などの自然変数で表現し、導出を行えるようにすることである。
例えば、等温膨張(#DeltaT = 0, DeltaV > 0#)からエントロピーを計算するには、#V_2#と#V_1#、あるいは#P_2#と#P_1#、そして単原子理想気体の場合を知っていればいいのである。
#DeltaS = -nRln(P_2/P_1) = nRln(V_2/V_1)#
- Ideal and Nonideal Non-Electrolyte/Electrolyte Solutions
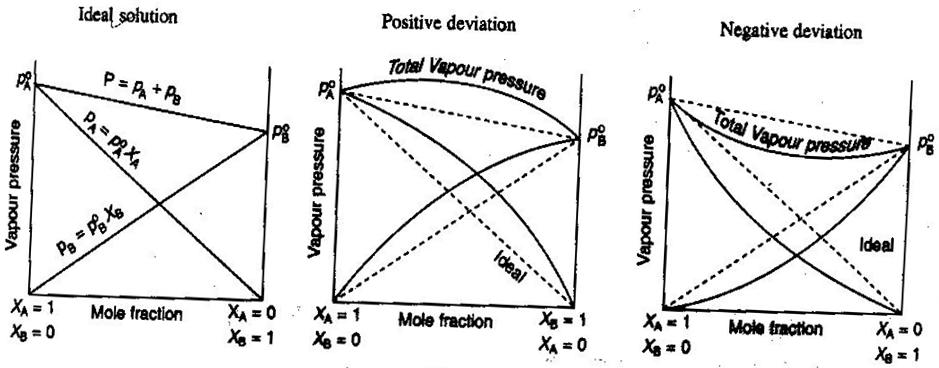
一般化学で、”DeltaS=0 “であることが知られています。 溶液は理想的に扱いたいもので、体積は相加平均、強電解質の濃度はまっすぐ#”mol/L “#で計算する、といった具合に。
- 溶液を混ぜると膨張したり収縮したりします。
- イオン対は溶液のイオン強度を下げ、溶質のファントホッフ係数#i#を下げます。
- 溶質の逃避傾向は、その有効濃度(活性)を変化させます。
KINETICS
一般化学の授業で、あるいは高校でやったことがあるかも知れませんね。 物理化学では、これをもう少し発展させて、反応機構や気相のダイナミックスを詳しく見ていきます。
2つの例:
- Steady-State approximation
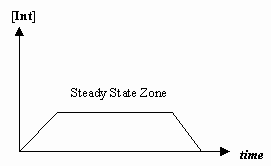
時には最初のメカニズムの段階の速度が2段階目の速度よりずっと遅く、中間体の濃度が実質的に変化しない (#(d)/(dt) = 0#) という近似をすることがあります。
これにより、機構に特有の速度則が導出され、個々のステップの速度定数で「観測された速度定数」を表現することができるようになるのです。
- Real Gas Laws
van der Waalsの状態方程式は紹介したことがあるかもしれません:
#(V – nb) = nRT#
まあ他にもレッドリッチ・クウォン、ペン・ロビンソンなどなどありますけども。
基本的な考え方は、特定の気体では他の気体よりもよく働くが、すべての気体が弾性衝突する不活性な点質量であると仮定するのではなく、気体の実際の特性を説明するために働くということです。
STATISTICAL MECHANICS
統計力学では、マクロな視点からピコスコープの世界を見て、一歩後退するのです。
「粒子の大きな集合体について量子化学者のように考えると、システムから何がわかるだろうか?”
二つの例:
- Equipartition Theorem
#<K > = N/2nRT = N/2 k_BT#,
ここで #N# は運動の種類(直線、回転、振動、電子、核)の自由度数であり、それぞれの運動が何度あるのか? 基本的には分子のあらゆる運動を考慮して、その平均運動エネルギー#<< K >># を推定する。
これは「十分に高い」温度でのみ有効です。 通常、並進運動や回転運動には問題ないが、振動の寄与を過大評価する傾向がある。
- The Microcanonical Partition Function
#q = sum_(i=1)^(N) g_ie^(-beta epsilon_i)#,
where:
- #g_i# is the degeneracy of state #i# with energy #epsilon_i#.
- #N# は利用可能な状態の総数である。
波動関数#psi#が量子力学系について知るべきことをすべて規定しているように、ミクロカノニカル分割関数は分子が利用可能なエネルギーをどのような種類の状態(並進、回転、振動、電子、核)に分配できるかを規定しています。 #q_(tr)#, #q_(rot)#, #q_(vib)#, #q_(el ec)#, #q_(n uc)#.
それぞれの#q#を知ることにより、エントロピー (#S#), エンタルピー (#H#), Gibbsの自由エネルギー (#G#) などの熱力学量もそれぞれの#q#で導き出せるようになる。
便利な例として、ほとんどの場合、任意の温度での絶対分子エントロピーは次のように計算できる:
#S/N = k_B ln (q/N)_”tot” + (<< epsilon >_”tot”)/T + k_B#,
ここで:
- #k_B ~ ~ “0.695 cm”^(-1)”/K “# はボルツマン定数。
- #(q/N)_”tot” = (q_(tr))/Nq_(rot)q_(vib)q_(el ec)q_(n uc)# は考えられるすべてのタイプの状態を含む全ミクロカノン分割関数、#N# は考慮する分子の全数です。
- #<>> = E/N# は分子エネルギーで、#<<イプシロン>> = k_BT^2((del ln (q”/”N)_”tot”)/(del T))_V# として定義されます。
(そう、#”298.15 K “#でのこの式で、教科書の付録にあるのと同じ#S^@#を計算できるのです!)
この式の使用例はこちらでご覧になれます。