La chimie physique est un sujet quelque peu vaste ; elle couvre :

• La chimie quantique
• La thermochimie (révision + plus)
• La cinétique (révision + plus)
• La mécanique statistique

Comme il y a pas mal de sujets pour une réponse, je ne donnerai que deux exemples par sujet. Cela va être une longue réponse, mais vous pouvez vous concentrer sur ce que vous recherchez.

ChIMIE QUANTUMIQUE

La chimie quantique consiste généralement à essayer de comprendre des scénarios à l’échelle picoscopique, en modélisant les systèmes dans des représentations mathématiques commodes et en faisant les approximations appropriées.

Deux exemples de chimie quantique sont :

• Oscillateur harmonique simple (deux billes reliées par un ressort idéal)

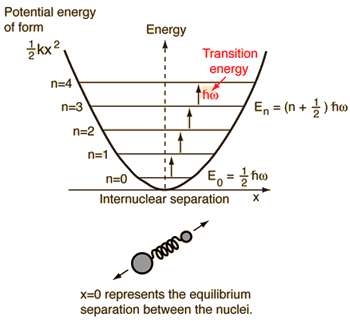
Pour ce système, que nous connaissons de la physique, nous le réduisons d’un problème classique à deux corps à un problème à un corps avec des coordonnées relatives et une masse réduite, #mu = (m_1m_2)/(m_1 + m_2)#.

Ce système est axé sur la compréhension de l’énergie potentielle élastique de la liaison moléculaire.

• Rotor rigide (deux boules reliées par une tige, c’est-à-dire un ressort 100% rigide)

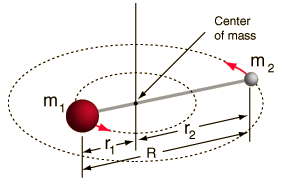
Ce système est une simplification, car toutes les molécules ont une forme d’étirement/vibration de la liaison (vous comprendriez pourquoi cette simplification est OK, si vous voyiez les maths !).

Cependant, il nous permet de décomposer cette composante angulaire d’un système à deux corps et de comprendre les propriétés rotationnelles de la molécule.

THERMOCHEMISSIE

Ceci s’intéresse à l’échelle macroscopique du flux de chaleur, du travail, des énergies libres, et ainsi de suite. Vous l’avez déjà fait dans la chimie générale en quelque sorte, et cela est revu et développé.

Deux exemples sont:

• Détermination des valeurs thermodynamiques à partir de grandeurs mesurables

Qu’est-ce que la chimie si elle n’est pas pratique ?

Donc, un thème commun est de pouvoir effectuer des dérivations et exprimer les principales quantités thermodynamiques (entropie, enthalpie, énergie libre de gibbs + helmholtz, énergie interne) en termes de variables naturelles comme le volume, la température et la pression.

Par exemple, on peut calculer l’entropie à partir d’une expansion isotherme (#DeltaT = 0, DeltaV > 0#) en connaissant #V_2# et #V_1#, ou #P_2# et #P_1#, et cela pour un gaz idéal monatomique :

#DeltaS = -nRln(P_2/P_1) = nRln(V_2/V_1)#

• Solutions non électrolytes/électrolytes idéales et non idéales

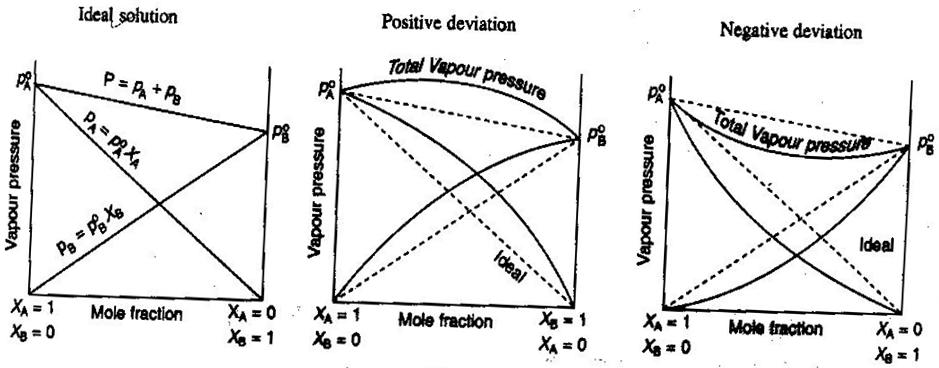
En chimie générale, nous aimons traiter les solutions idéalement, de sorte que les volumes s’additionnent, les concentrations d’électrolytes forts sont des calculs directs # »mol/L « #, et ainsi de suite. Quelques façons dont les solutions peuvent ne pas être idéales:

• La solution peut se dilater ou se contracter après avoir été mélangée.
• L’appariement des ions diminue la force ionique de la solution et réduit le facteur de van’t Hoff #i# du soluté.
• La tendance à l’échappement du soluté modifie sa concentration effective (son activité).

KINÉTIQUE

Vous avez peut-être déjà fait cela dans un cours de chimie générale, ou peut-être au lycée. La chimie physique s’étend un peu plus sur ce sujet en examinant les mécanismes de réaction et la dynamique de la phase gazeuse de manière plus détaillée.

Deux exemples :

• Approximation de l’état stationnaire

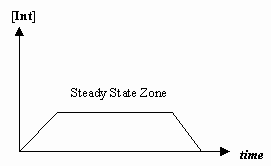
Parfois, la vitesse de la première étape mécaniste est beaucoup plus lente que celle de la deuxième étape, et nous faisons l’approximation que la concentration de l’intermédiaire ne change effectivement pas (#(d)/(dt) = 0#).

Cela permet de dériver une loi de taux particulière à un mécanisme, et de nous permettre d’exprimer une « constante de taux observée » en termes de constantes de taux pour les étapes individuelles.

• Les lois réelles des gaz

On vous a peut-être présenté l’équation d’état de van der Waals :

#(V – nb) = nRT#

Bien, il y en a d’autres, comme celle de Redlich-Kwong, de Peng-Robinson, etc.

L’idée de base est qu’ils fonctionnent tous mieux pour certains gaz que d’autres, mais ils fonctionnent tous pour rendre compte des propriétés réelles des gaz au lieu de supposer que tout le monde est une masse ponctuelle inerte à collision élastique.

MÉCANIQUE STATISTIQUE

Avec la mécanique statistique, nous prenons du recul et regardons le monde picoscopique d’un point de vue macroscopique :

« Que peut-on apprendre d’un système si on pense comme un chimiste quantique à une grande collection de particules ? »

Deux exemples :

• Théorème d’équipartition

#<< K >> = N/2nRT = N/2 k_BT#,

où #N# est le nombre de degrés de liberté pour chaque type de mouvement (linéaire, rotationnel, vibrationnel, électronique, nucléaire). Fondamentalement, il prend en considération chaque type de mouvement dans une molécule pour estimer son énergie cinétique moyenne, #<< K >>#.

Cela ne fonctionne qu’à des températures « assez élevées ». Habituellement, c’est OK pour les mouvements de translation et de rotation, mais cela a tendance à surestimer les contributions vibratoires.

• La fonction de partition microcanonique

#q = somme_(i=1)^(N) g_ie^(-beta epsilon_i)#,

où:

• #g_i# est la dégénérescence de l’état #i# avec l’énergie #epsilon_i#.
• #N# est le nombre total d’états disponibles.

Tout comme la fonction d’onde #psi# spécifie tout ce qu’il y a à savoir sur un système de mécanique quantique, la fonction de partition microcanonique spécifie comment une molécule peut distribuer son énergie disponible dans les types d’états possibles (translationnel, rotationnel, vibrationnel, électronique et nucléaire).

Il existe un #q# pour chaque type d’état : #q_(tr)#, #q_(rot)#, #q_(vib)#, #q_(el ec)#, et #q_(n uc)#.

De la connaissance de chaque type de #q#, les quantités thermodynamiques familières peuvent être dérivées, telles que l’entropie (#S#), l’enthalpie (#H#), l’énergie libre de Gibbs (#G#), et ainsi de suite, en fonction de chaque type de #q#.

A titre d’exemple utile, l’entropie moléculaire absolue à TOUTE température dans la plupart des cas peut être calculée comme:

#S/N = k_B ln (q/N)_ »tot » + (<< epsilon >>_ »tot »)/T + k_B#,

où:

• #k_B ~~ « 0.695 cm »^(-1) »/K « # est la constante de Boltzmann.
• #(q/N)_ »tot » = (q_(tr))/Nq_(rot)q_(vib)q_(el ec)q_(n uc)# est la fonction de partition microcanonique totale qui inclut tous les types d’états possibles, et #N# est le nombre total de molécules considérées.
• #<< epsilon >> = E/N# est l’énergie moléculaire, définie comme #<< epsilon >> = k_BT^2((del ln (q »/ »N)_ »tot »)/(del T))_V#.

(Oui, cette formule à # »298,15 K « # vous permet de calculer le même #S^@# que vous voyez dans l’annexe de votre manuel !)

Un exemple de cette formule en utilisation peut être trouvé ici.